Основные параметры процесса наполнения

Основные параметры, характеризующие процесс наполнения, – давление и температура заряда в начале сжатия Р_а, Т_а. Их принимают в качестве исходных для расчета давления и температуры заряда в процессе сжатия. При выполнении теплового расчета методом Гриневецкого-Мазинга P_а определяют ориентировочно на основании экспериментальных данных о соотношениях между давлением рабочей смеси в конце наполнения и давлением воздуха перед впускными органами: , где Р_s – давление наддува.

Судовые ДВС имеют следующие значения отношения давления заряда в начале сжатия к давлению наддува:

4- тактные без наддува (тихоходные): = (0,850,95);

4- тактные без наддува быстроходные: = (0,800,90);

4- тактные с надддувом: = (0,851,1);

2- тактные с прямоточно-клапанной продувкой: = (0,91,1);

2- тактные с контурной продувкой: = (0,851,05).

Температуру заряда в начале сжатия определяют из теплового баланса заряда в начале сжатия и допущения о равенстве теплоемкостей компонентов заряда.

Принимая ;

, разделив обе части уравнения на , получим

;   , (34)

Т – подогрев воздуха от стенок цилиндра.

Т = 5 - 10 ^С у 2- тактных, Т = 5-20 ^С у 4- тактных двигателей,

Т_r = 700 - 800 К.

Так как _r мало, Т_r относительно мало влияет на Т_а.

Коэффициент наполнения судовых ДВС имеет следующие значения:

_н

4- тактные без наддува тихоходные 0,800,90;

4- тактные без наддува быстроходные 0,750,85;

4- тактные с наддувом 0,850,95;

2- тактные (к полному ходу поршня) 0,650,85.

23 вопрос Процесс сжатия

3.2. Процесс сжатия

В процессе сжатия достигается температура, достаточная для самовоспламенения топлива. Происходит процесс при движении поршня от НМТ к ВМТ после закрытия органов газообмена (клапанов, окон). Параметры, характеризующие процесс сжатия: показатель политропы сжатия n₁, P_с, T_с, .

При отсутствии утечек воздуха и теплообмена процесс сжатия проходил бы по линии ас¹ (рис. 17), согласно уравнению , где k₁ – показатель адиабаты сжатия. Но сжатие – сложный процесс, зависит от теплообмена между воздухом и стенками переменного по величине и знаку. В начале сжатия идет подогрев воздуха – k₁. В точке 1 температура воздуха становится равной средней температуре стенок, = k_1. При дальнейшем сжатии температура воздуха становится больше температуры стенок k₁.

В результате давление конца сжатия (точка с) действительного процесса меньше давления конца сжатия адиабатного процесса (точка с¹). Около ВМТ n₁, оставаясь ниже k₁, несколько увеличивается, т.к. в конце сжатия уменьшается поверхность охлаждения, заряд соприкасается с более нагретыми деталями, что уменьшает теплоотдачу в стенки, а также начинается тепловыделение от сгорания.

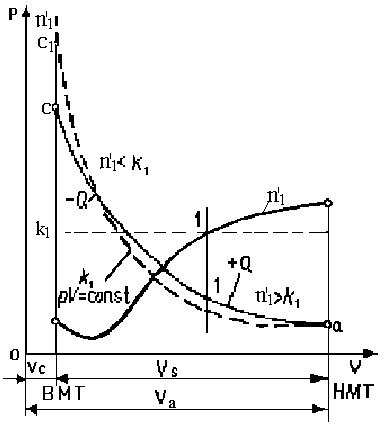
Рис. 17. Схема процесса сжатия

Утечка воздуха через неплотности колец невелика и незначительно снижает Р_с и Т_с, поэтому ее, как правило, не учитывают. В расчетах полагают, что процесс происходит по политропе с условным средним показателем n₁, который выбирают так, чтобы получалась такая же работа при сжатии, что и при истинном переменном показателе. Из опыта: МОД с охлаждаемыми поршнями n₁ = 1,34-1,38, СОД и ВОД n₁ = 1,38-1,42.

Средний показатель политропы сжатия можно определить по уравнению политропы и индикаторной диаграмме:

;     . (35)

При проектировании ДВС средний показатель политропы сжатия получают из уравнения баланса теплоты за процесс сжатия. При этом принимают допущение, предложенное Мазингом: количество теплоты, сообщенное воздуху в процессе, равно нулю, т.е. процесс сжатия рассматривается как псевдоадиабатический. При этом средний показатель политропы будет равен показателю кажущейся адиабаты. Уравнение первого закона термодинамики:

, (36)

где – количество теплоты, подведенное воздуху в процессе сжатия в результате теплообмена со стенками цилиндра, = 0 по допущению;

– изменение внутренней энергии рабочей смеси в процессе сжатия; – количество теплоты, эквивалентное абсолютной работе политропного сжатия на участке ас:

; (37)

; (38)

где – постоянные коэффициенты.

Учитывая , получим . (39)

Это уравнение решают методом последовательных приближений, задаваясь n₁ = 1,34÷1,42 и добиваясь тождества после решения. Р_с и Т_с определяют из уравнения политропы сжатия:

;    ;    . (40)

У современных ДВС: Р_с МПа Т_с К

без наддува 3,5÷5 700÷900

с наддувом 4,0÷11,0 850÷1100.

24 вопрос Процесс сгорания