Вопросы к экзамену по алгебре.

1.Тождество.

2.Тождественно равные выражения.

3.Тождественные преобразования выражений.

4.Область допустимых выражений.

5.Уравнение.Корни уравнения.

6.Свойства уравнений.

7.Что значит –решить уравнение?

8.Линейное уравнение с одной переменной.

9.Свойства линейного уравнения с одной переменной.

10.Простейшие уравнения, содержащие знак модуля.

11. Решение линейного уравнения с одной переменной.(все случаи)

12.Линейное уравнение с двумя переменными.

13.Свойства линейного уравнения с двумя переменными.

14.График линейного уравнения с двумя переменными.

15.Системы двух линейных уравнений с двумя переменными. Что называется

решением системы двух линейных уравнений с двумя переменными?

16. Решение системы двух линейных уравнений с двумя переменными.(все случаи)

17.Способы решения системы двух линейных уравнений с двумя переменными.

18.Функция .Способы задания функции.

19.График функции.

20.Линейная функция , её график, смысл коэффициентов.

21.Прямая пропорциональность , её график.

22. Условие параллельности графиков линейных функций.

Задачи к экзамену:

1.Вычислить:

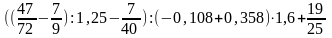
2. Упростить выражение

,

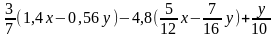найти его значение, если –x+1,4y=-0,25.

3. Кусок сплава золота с серебром , содержащий 30% серебра сплавили куском , содержащим 10% серебра и получили 600 г сплава содержащего 85% золота . Сколько граммов 10%-ного сплава было взято?

4.Трехзначное число оканчивается цифрой 4. Если эту цифру переставить на первое место, то число увеличится на 243. Найдите трехзначное число.

5.Решить уравнение:

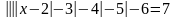
6.Турист выехал на мотороллере из А в В со скоростью 50 км/ч. Через 24 мин после отправления из А он должен был снизить скорость на 10 км/ч , так как дорога пошла в гору , и поэтому прибыл в В на 18 мин позже , чем предполагал. Чему равно расстояние между пунктами А и В?

7.Бассейн объемом 1800 куб.м первая труба заполняет за 12 часов , вторая труба в 1,5 раза медленнее , чем первая. При наполнении бассейна сначала включили вторую трубу , через 1,8 часа включили первую . Сколько времени работала вторая труба?

8.Решить уравнение:

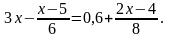
9.На соревнованиях по гребле спортсмен проплыл расстояние между пунктами А и В по течению реки за 15 минут, а против течения реки из В в А за 20 минут . Какова скорость течения реки если лодки в стоячей воде 14 км/ч?

10.Решить уравнение:

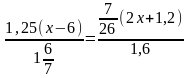
11.Решить уравнение:

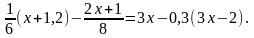
12.На склад завезли 720кг овощей. Количество овощей отпущенных со склада в первый день относится к количеству овощей отпущенных со склада в третий день как 3:5 , во второй день было отпущено на 20% меньше , чем в третий , после чего на складе осталось 96 кг овощей. Сколько кг овощей отпущено со склада в первый день?

13.Имеются два сплава, первом из которых содержится 40% серебра, а во втором-20% серебра . Сколько кг второго сплава необходимо добавить к 20 кг первого сплава , чтобы получить сплав , содержащий 30% серебра?

14.Расстояние от А до В поезд проходит за 2 часа . Если скорость поезда увеличить на 25 км/ч, то уже через 1,5 часа после выхода из А ему останется пройти до В 10 км. Найти расстояние от А до В?

15.Решить уравнения:

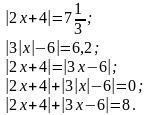
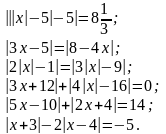
16.Решить задачи:

1. Сплавили два слитка, содержащие золото и серебро и получили слиток, содержащий 20% золота. Первый слиток содержит 10% золота, второй-25% золота. Какова масса полученного сплава, если известно , что масса второго слитка на 3 кг больше массы первого?

17. Сплавили два слитка, содержащие золото и серебро и получили слиток, содержащий 20% золота. Первый слиток содержит 10% золота, второй-25% золота. Какова масса полученного сплава, если известно , что масса золота во втором слитке на 3 кг больше массы золота в первом слитке?

18.Найти ОДЗ выражения:

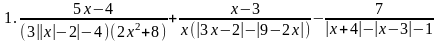
19.Выполнить тождественные преобразования выражения:

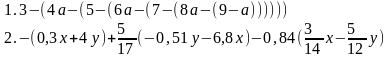
20. Дополнить недостающим:

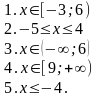
21.При каких значениях параметров а и b уравнение

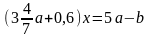
имеет одно решение? Найти это решение.

22.При каких значениях параметров а и b уравнение

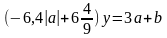
не имеет решений?

23.При каких значениях параметров а и b уравнение

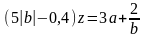
имеет бесконечно много решений?

24.Решить уравнение с параметрами:

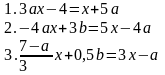
25.Выполнить тождественные преобразования:

1.3(4-x)-(2(x+1)-5(x-7))

2. 7(2y-x)-((5y-3x)-4(x+y))

3.-0,45(6 )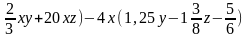

4.Докажите тождество:

xy(1-z)-yz(1+x)-xz(1-2y)=xy-yz-xz

5.Докажите , что при всех значениях переменной, выражение имеет одно и тоже значение:

7(1-y)-6(1-2y)+5(11-y)

26.Решить уравнения:

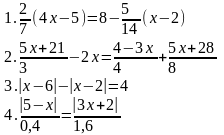
27.Найти ОДЗ выражения:

1.

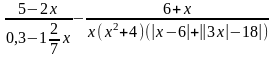
2.

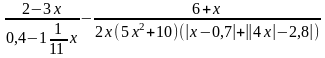
28. Выполнить тождественные преобразования выражения

1,6(2x-3y)-3(2,3x+1,2y) и найти его значение при x=-10, y=0,1.

29. Решить уравнение:

5-6(2x-4)=5x+4.

30. Найти ОДЗ выражения:

.

31. Решить задачу:

Класс разделили на две подгруппы, причем в первой подгруппе в 1,5 раз больше учащихся , чем во второй. После того , как 3 человека перевели из первой подгруппы во вторую количество человек в подгруппах стало равным. Сколько человек в классе?

32. Решить задачу:

Велосипедист ехал по маршруту АВ со скоростью 16 км/ч ,а возвращался по другой дороге , длина которой на 6 км больше, со скоростью 18 км/ч. На обратный путь он затратил на 7,5 минут больше времени. Найти длины обеих дорог.

33. Решить уравнения:

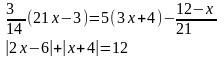
34. Найти ОДЗ выражения:

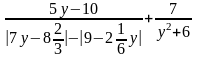
35.Решить уравнение:

.

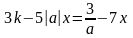36. Решить задачу:

Имеются два сплава из цинка , меди и олова. Известно , что первый сплав содержит 40% олова , а второй- 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго , получили новый сплав, в котором оказалось 30% цинка .Сколько кг олова содержится в полученном сплаве?