2. Динамическая модель однопродуктовой фирмы, предельные издержки которой постоянны

Допустим Х₀ – это деньги, взятые предприятием в долг, а К₀ – это оборудование, купленное на эти деньги. Следует отметить, что К₀ = γ Х_0,

( γ так как деньги, взятые в долг в банке не все идут на покупку оборудования. ( )

Также предположим, что процесс производства происходит в какой-то момент времени t. Тогда K_t – это основные фонды в момент времени t. Тогда количество производимой продукции в момент времени t будет равен

Q_t = λK_t , доход тогда будет равен R = PQ_t , а издержки C_t = c + nQ_t .

Из имеющихся данных мы можем вычислить прибыль, получаемую предприятием в момент времени t.

Π_t = PQ_t - c - nQ_t

Предприятие тратит свою прибыть обычно в трех направлениях:

Π_t = I_t + A + Z , где I_t – инвестиции в производство в момент времени t,

A – часть долга, выплачиваемая в фиксированный период времени,

Z – собственный потребительские расходы предпринимателя,

Предположим, что A, Z - const, тогда долг в последующий момент времени t+1 будет равен: X_t+1 = X_t + αX_t – A (1)

(долгу в предыдущий момент времени + проценты взимаемые с данного долга в момент времени – выплачиваемая часть долга, где α – процентная ставка, под которую взят кредит).

Из формулы прибыли следует Π_t = Qt(P - n) – c =>

• Π_t = λK_t (P - n) – c

Тогда основные фонды в будущий период времени t+1 будут равны

K_t+1 = K_t + ((P-n) λK_t –c) - μK_t , где μK_t – затраты на износ оборудования

• K_t+1 = K_t (1+ (P-n) λ - μ) –c (2)

Из этого мы получаем систему двух линейных уравнений:

X_t+1 = X_t β – A, где β = 1+α

1. Рассмотрим случай, когда А (выплаты по кредитам) таковы, что долг не изменяется, он постоянен. Если А = 0, то долг будет увеличиваться.

Тогда X_t = const = – равновесное значение долга

, отсюда находим А (долг в момент времени)

,

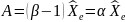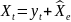, из формулы (1) следует, что

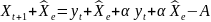, после сокращения получаем

, отсюда можно сделать вывод: для того, чтобы долг уменьшался необходимо, чтобы y₀ < 0, а х₀ <

2. Определим период погашения долга (находим время t) , то при Х_t = 0

=>

=>

возьмем целую часть и прибавим единицу, т.к. в последний месяц долг будет меньше, чем А. Получим:

(3)

3. Как повысить потребительские расходы предпринимателя (Z)

Допустим, из формулы (2) b = 1+ (P-n) λ _– μ , то K_t+1 = K_t b – c

Если К_t = const = , то

= b – c =>

=>

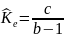
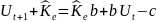=> (4)

Из уравнения (4) следует, что должно быть равно 0, тогда => U_t = U₀b^t , при этом b должно быть b > 0 , тогда

(P-n) λ > μ , т.к. (b-1)

μ –коэффициент выбытия

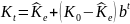, при этом К₀ > ,

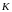
3.Простейшая модель экономического роста – модель мультипликатора

В модели Дж. Кейнса рассматривается один макроэкономический рынок – рынок товаров. При этом следует отметить то, что рынок не находится в равновесии:

модель описывает процесс установления равновесия.

Эффект мультипликатора состоит в том, что увеличение инвестиций приводит к увеличению национального дохода, который возрастает в гораздо больших размерах, чем первоначальный рост автономных расходов (автономного потребления, автономных инвестиций,

государственных закупок).

Содержание мультипликатора отражено в первичном значении слова.

Multum– первая составная часть сложных слов, указывающая на множественность, многократность. Вторая часть слова – plicare – складывать, сгибать, сворачивать. Если суммировать: мультипликатор – умножитель.

Итак, мультипликатор (m) это коэффициент, который показывает во сколько раз величина изменения ВВП будет больше величины изменения автономных расходов.