2.4. Примеры неодносвязных областей существования режима

В [6, 7] были построены области, когда возможно пол­ное аналитическое исследование всего пространства. Эти случаи характеризуются значительным упрощением задачи, поскольку предполагалось, что одна из проводимостей рав­на нулю. Ниже приводятся общие случаи, когда все прово­димости отличны от нуля. Поскольку при этом нет возмож­ности провести анализ в общем виде, то построение области существования режима осуществлялось на основе численных расчетов.

Для системы

Р_х=А_Х2 sin(61—62—СС12) 13 sin(61—63—GC13),

Р₂=А\2 sim(6₂—'61—a_i2) +^23 sin(б₂—63—а₂з)

при параметрах А\₂=1, А_]3=А₂₃=а, а=0,05, 0,1; 0,5, ai2= = —я/6, ai3=a₂3, варьируя значения углов 61 и 62 (6з = 0), вычислялись значения Р_и Р₂ по приведенным выражениям. При этом для 6₂=const; 6i = fe[—я, я] получаем на плос­кости Р_и Р2 эллипсы, которые с изменением б2 перемещают­ся по плоскости. Для а=0,05 область существования режи­мов имеет внутри большую полость, в которой режимы не

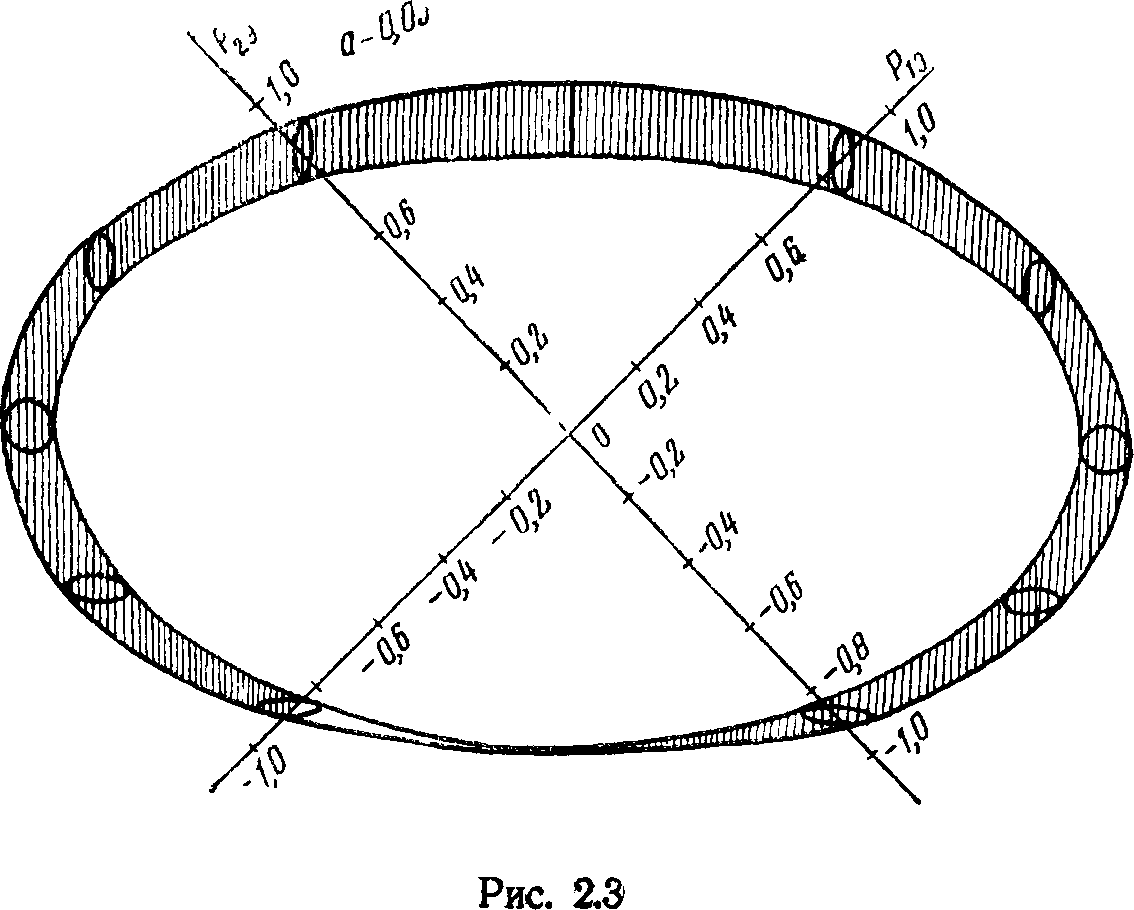
существуют (>рис. 2.3). По мере увеличения а (рис. 2.4) са­ма область существования режимов по размерам увеличива­ется, а внутренняя полость сжимается. При а=0,87 внут­ренняя шолюсть исчезает, область существования ре­жимов «становится односвязной Так как в рассматривае­мых случаях P_l3 = P₂₃ = a, ai₃=a23=a, то области сущест­вования режимов во всех случаях оказываются симметрич­ными относительно биссектрисы первого координатного уг­

ла. Это можно доказать и аналитически. Действительно, уравнения режима имеют вид

p_1=sin^Si—б₂+ а),

Р i=sin

P₂=sin sin (б₂— а).

Рис. 2.4

Если в эт.их уравнениях заменить индексы 1 на 2, а 2 на 1, то система примет вид

P₂=sin^₂— 61+ ~-)+asin(S₂—а).

61—б₂+ yj+asin(6i~a).

Последняя система совладает с предыдущей, поэтому и область существования режимов при перемене осей должна сохранить свой вид, а это означает, что эта область имеет

37

ось симметрии, проходящую через биссектрису первого ко­ординатного угла.

Построение областей существования режимов осуществля­лось по результатам численных расчетов отображения цик-

Рис. 2.5

лов 6i = const; и 62=const. На рис. 2.3 и 2.4 показаны лишь образы циклов 6i2=const, граница области проведена как огибающая такой системы эллипсов, область заштрихована. На рис. 2.5 показаны как образы циклов 6i2=const, так и образы циклов 62=const; огибающая здесь не построена, чтобы не усложнять и без того сложный рисунок, область существования режимов не штрихуется.

3. Область существования режимов в пространстве реактивных мощностей при постоянных эдс узлов

В дополнение к рассмотренному выше пространству ак­тивных мощностей рассмотрим пространство реактивных мощностей, которые определяются следующими соотношени­ями:

л-И

Qi=E?y_H cos а, — S Е£_ку_ш cos (б<—6*—a_ih), (3.1)

к = 1 к Ф1

ь 1, 2, П¹,

где опять будем считать, что Е_{ (i= 1, 2,...,/i+l) постоянны, 6_n+i = 0, (п+'1)-я станция — балансирующая. Такая поста­новка задачи, по-видимому, не имеет самостоятельного зна­чения, но важна для дальнейшего исследования множества

режимов 'в пространстве полных мощностей &=/Vf-/Q«» ^к0" торое рассматривается ниже.

Обозначим

qt₃= qt ^]е?ун cos ccit, au = a_kh= о,

Ai_k—EiE_hy_ih

при гфк.

Тогда рассматриваемая система примет вид

/7-4-1

Qi₃=— 2 Л_гАсо5(бг—б_А— a*), i= 1, 2,...,/г. Обозначим

—— э

при этом

cos (8г—б_А— a_ik) = — .Sin (6г^б_А—'М,

и уравнения для реактивных мощностей примут вид

л+1

Qo=2 A_ik sin(6<— 8_k—Р<_А),

'Ь lj 2, t%»

Эта система имеет вид аналогичный системе, рассмотрен­ной для пространства активных мощностей. Поэтому все ут­верждения, сформулированные для Р_1э, Р_2э, ...» Рп₈, имеют силу и для Q_b, Q_2a, •••> Qn₃ при замене в них a_tft на

Множество всех режимов в пространстве Qu Q2, Qn при фиксированных Е_и £₂, ..., Е_п «есть ограниченное замкну­тое связное множество, прообразом которого является гипер- тор {—я^бг^я, i= 1, 2, ..., /г}. Число и род критических точек функций, зависящих от реактивных мощностей и уг­лов 6_г, совпадают с числами Бетти для гипертора соответст­вующей размерности.

Область существования режимов в пространстве Qi, Q₂, Q_n имеет центр симметрии в точке с координатами

Qi=Ei²y_t{ cos a,,, i=l, 2,..., п,

если для всех гфк углы р_гА=0. Рассмотрим линейные функции

п п

L(ii_y Q) = 2 fx_tQi= 2 |я_г[Е?у_а cos а«+2Л_Л sin (б,—»б_Л—p_ffc) ].

1 i = 1 /г

Обозначим

sup Q)=M(|i),

{5_lt Й_а, ... , S^J

inf L(ji, Q)=m(|i).

{S[, 5_a,... , 5_W}

Тогда в полупространстве

2 QilXi>M(ix) 1

нет точек, принадлежащих области существования режимов.

Аналогично, нет точек, принадлежащих области сущест­вования режимов, и в полупространстве

п

Эти утверждения следуют из того, что рассматриваемые линейные формы на множестве режимов не могут принимать значений, превышающих наибольшее значение, и значений,

меньших наименьшего. Значения ikT(^t), т(jn) могут быть оп­ределены решением задачи на абсолютный экстремум для функции L(\i_y Q). Поскольку |3i2=0 соответствует условию

а₁₂= —> т. е. сети чисто активной, то аналог теоремы

2

3 [6] из раздела односвязности области существования ре­жимов имеет весьма узкое значение. Вместе с тем аналог теоремы 5 [6] оказывается весьма интересным.

Повторяя рассуждения этой теоремы для уравнений для реактивных мощностей, получаем: область существования установившихся режимов на плоскости реактивных мощно­стей (п=2) односвязна, если выполняется хотя бы одно из условий

^Л12 |sin2|3₁₂|<l, JilL|sin2p_lf|<l.

Aiz A 2s

Преобразуем эти выражения:

sin2 +

sin 2 а

12

sin 2 Р₁₂1 =

Таким образом, получаем теорему.

Теорема 3.1. Область существования установившихся режимов на плоскости реактивных мощностей (п—2) одно- связна, если выполняется хотя бы одно из условий

Л121 sin 2ai21 Л j₂| sin 2ai₂|

Итак, условия односвязности области существования ре­жимов в пространстве активных и реактивных мощностей для системы, содержащей 3 станции, совпадают.

Аналогично для системы, содержащей произвольное чис­ло узлов, область существования режимов в пространстве реактивных мощностей односвязна, если существует набор целых чи<Ьел р_к^(т)= 0, 1, таких, что удовлетворяются одно­временно п неравенств:

п

А_туп+i 2 cos PkWft'Amh sin 2a_ftm у т== 1, 2,..., п.

Таким образом, условия односвязности области сущест­вования режимов и в пространстве Р_и Р₂у ..•> Р_Пу и в прост­ранстве Qi, Q₂, Q_n одинаковы.

Перейдем к формулировке теорем, оценивающих разме­ры области существования режимов в пространстве реак­тивных мощностей.

Теорема 3 2. Признак неразрешимости системы. Если существует ненулевой вектор |^={|Ыь \x_2i Цп}, такой, что выполняется хотя бы одно из неравенств

^iQi+R₂Q2+ ... +linQn>M(ii)_y (3.2)

LiiQi + ^₂Q₂+ ... (3.3)

то система уравнений (3.1) не имеет действительных реше­ний, т. е. при заданных значениях параметров сети и реак­тивных мощностей Qi, Q₂, ..., Q_n не существует установивше­гося режима рассматриваемой электрической системы.

Доказательство непосредственно вытекает из утвержде­ний, сформулированных на с 13

Пусть теперь "выбраны г неколлинеарных векторов:

М_г= sup L(|a«, Q); m_t= inf Q).

{Si, 6_3I , 5^} {6t, 6₂, . . , &_nJ

Тогда получаем многогранник, целиком содержащий все множество режимов.

Теорема 3 3. Область существования режимов в прост­ранстве реактивных мощностей при фиксированных напря­жениях узлов системы принадлежит внутренности многогран­ника, задаваемого неравенствами

m₂^ii^Qi + ii2^{2>Q2+ ... +\lnWQn^M_2i

+ ... ' (3.4)

Для определения m_x, М_г необходимо для каждого вектора решать задачи на экстремум. Для сокращения расчетов и получения быстрых оценок области существования решений могут быть полезны оценки чисел т_и М_г. Они получаются из рассмотренных выше заменой a_th на и с учетом того, что

2р_гь=2си+я,

cos 2fi_lk= —cos 2a_lk.

Итак,

M (jli) = 2 А_1кУ[1_г²+11и²+^г11_к cos 2а(3.5)

i<k

и в частности при a_lh—0

M(_VL)=2A*\_VL_t+_VL_k\. (3.6)

Kk

При этом

ЛГ(цЮ) =M_h,

m(ii(^k))=m_k^—M_h.

А потому многогранник, задаваемый неравенствами (3.4), целиком содержится в многограннике

—M_w<2|x.^(m)Q<<Afm, m= 1, 2, г. (3.7)

i

Таким образом, -получаем теорему.

Область существования режимов системы (3.1) в прост­ранстве Q1, Q₂, Q_n содержится в многограннике, опреде­ляемом неравенствами

т= 1, 2,г.

i

Простые выражения для постоянных М_т позволяют без затруднений бтроить такие многогранники при любом числе узлов.