5.7. Повышение пропускных способностей сетей, содержащих контуры* с нечетным числом ветвей

Рассмотрим исследованную выше сеть, показанную на рис. 5.17. В этой сети пропускная способность линий, подхо­дящих к узлу 1, не может быть реализована полностью. Но возможны мероприятия, которые позволяют в определенном смысле снять эти недостатки.

Рис. 5.18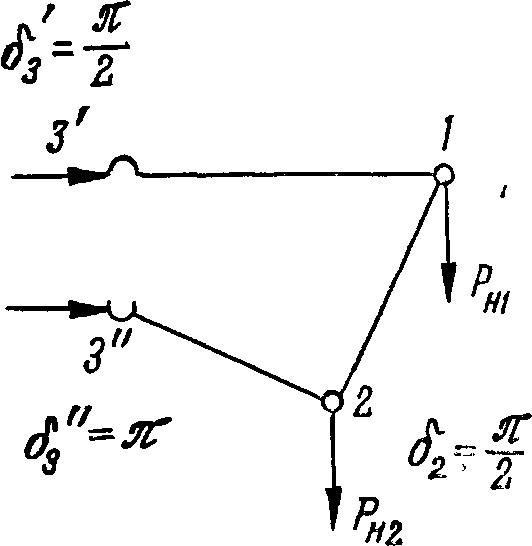

Расщепление генерирующего узла как мероприятие по повышению пропускных способностей сечений сети. Проведем

секционирование (расщепление) источника энергии—узла 3, разделив генерирующие мощности е»го на две независимо ра­ботающие группы: одна —на линию З'—l, другая —на ли­нию 3"—2. При этом граф сети превратится в дерево и ста­нет возможным полное использование всех пропускных способностей при распределении фаз векторов напряжений, ука­занном на рис. 5.18. Тем самым достигается существенное повышение пропускной способности рассматриваемого сече­ния. Но надо иметь в виду, что секционирование сети обла­дает и отрицательными свойствами, которые следует учиты­вать при его использовании.

Повышение пропускных способностей сети с помощью фа­зового регулирования. В 60-е годы в МЭИ (М. Н. Розано­вым) и НЭТИ (В. М. Чебаном) были предложены способы повышения динамической устойчивости с помощью фазового регулирования. Для этого предлагалось переключать обмот­ки трехфазных трансформаторов так, чтобы с изменением группы их соединений в сеть вводились дополнительные фа­зовые сдвиги между векторами напряжений ее различных точек. Эти предложения затем были развиты в трудах В. М. Чебана и его сотрудников [10]. Появились разработки специальных трансформаторов, позволяющих регулировать поворот фазы вектора напряжений в широких пределах. Та­кие трансформаторы в [И] было предложено применять для регулирования взаимовлияния между сближенными цепями двухцепной ЛЭП с целью повышения ее пропускной способ­ности.

Покажем, что фазорегулирующие трансформаторы (ФР) можно применять также и для повышения пропускной спо­собности сети в целом, так как они позволяют компенсиро­вать неблагоприятные фазовые соотношения в незаполняе- мых сетях и добиться полного использования пропускных способностей всех ветвей сети.

В ветвь 3—1 рис. 5.19,а введем фазорегулятор ФР, про­дольное сопротивление которого для упрощения рассужде­ний будем считать равным нулю (например, его можно ком­пенсировать конденсаторными установками). При этом в точке 3' получим вектор напряжения E₃’, отличный от E₃ лишь по фазе на величину δ_ф:

e^jδφ , δ₃’=δ₃+δ_ф

Для достижения максимального потока мощности по вет­ви 3—1 δ_ф следует регулировать по следующему правилу: при увеличении потоков мощности по ветвям 3—2 и 2—1, когда суммарный угол по этим ветвям (δ₃-δ₂)+(δ₂+δ₁)= δ₃+δ₁ начинает превышать π/2 и в соответствии с синусо­идальной зависимостью мощность по ветви 3—1 начинает уменьшаться, надо ФР вводить отрицательный сдвиг по фа­зе так, чтобы бз+бф—5i = 53/—6i=т. е. бф=— —'«я—

где Р3-2, Р2-1 — мощности, протекающие по ветвям 3—2 и 2-1.

L U

Таким образом, можно поддерживать по ветви 3—1 мак­симально возможную мощность при любых потоках^I мощно-

Рис 5 19

сти по остальным ветвям, и в частности при максимально

возможных потоках, когда бз—62=62—61= — . В последнем

2

случае б_ф= ~и векторы напряжений узлов сети образу-

ют диаграмму, показанную на рис. 5.19,6, которая соответ­ствует режиму заполнения данной сети с ФР.

Для количественной оценки эффекта такого регулирова­ния рассмотрим области существования режима трехузловой сети при Ai2=3, Ais=4, Л₂₃=8 отн. ед. (рис. 5.19 и 5.20). На рис. 5.20 кривой 1 показана граница области при отсутст­вии ФР, рассчитанная™ формулам, данным в [12]. Много­угольник 2_У описывающий эту область, дает границу •возмож­ных режимов при наличии фазового регулирования. Введение

такого регулирования даетзаметное расширение области воз­можных режимов. Так, при Р₂=4 максимальная передавае­мая мощность к узлу 1 увеличивается с 5,8 до 7 ед., что дает приращение на 17%. При Р\ = Ь максимальная передаваемая мощность к узлу 2 увеличивается с 3,7 до 5 ед., т. е. более чем на 35%. В такой сети можно одновременно использо­вать пропускные способности всех ее ветвей.

В заключение заметим, что указанные меры по повыше­нию пропускных способностей сетей не опровергают получен­ных выше условий заполняемости, а развивают их. И сек­

—I

Рис. 5.20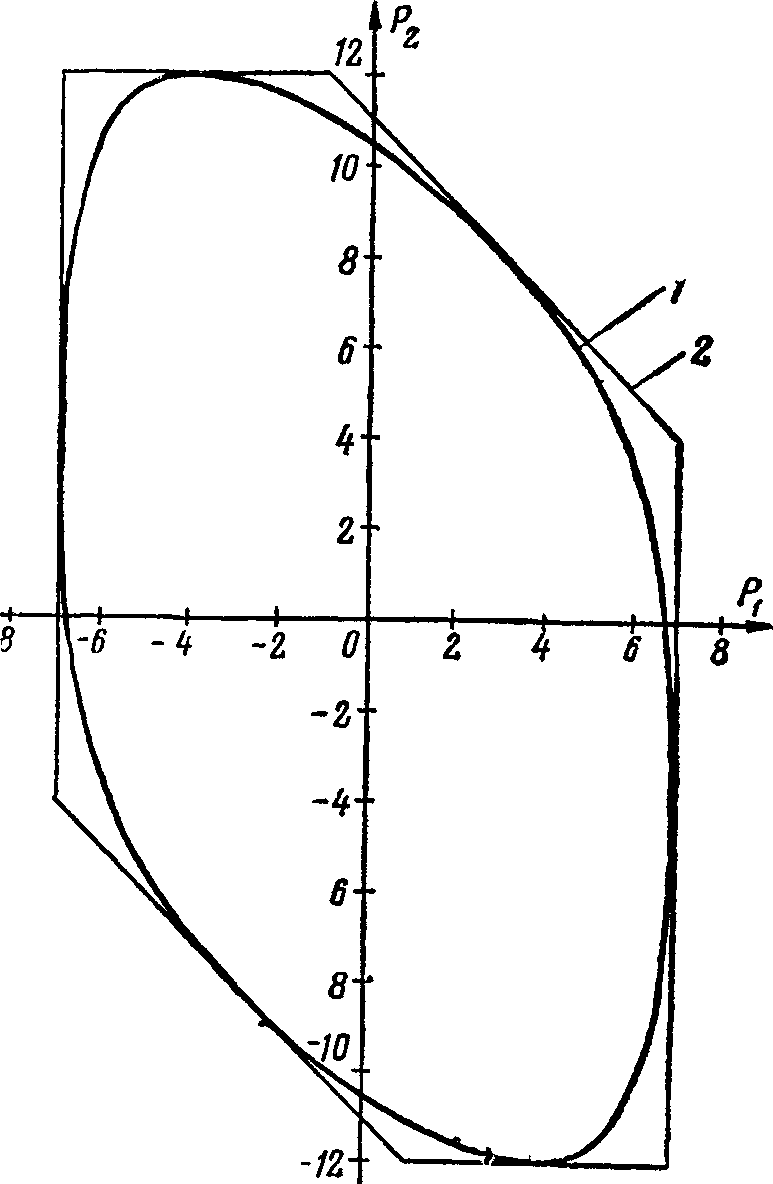

ционирование, и введение фазового регулирования переводят незаполняемую сеть в заполняемую: при секционировании граф сети становится деревом, введение фазорегулятора (рис. 5.19) по существу превращает сеть из трехузловой в четырехузловую с узлами У, 2, 3, 3Это показывает содер­жательность и практическую ценность рассмотренных выше теоретических положений и методов анализа.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА