
- •1. Проблемы анализа установившихся режимов электрической системы и области
- •1.1. Общие вопросы. Постановка задачи
- •1.2. Теоремы о выделении в (пространстве параметров области существования решений нелинейной системы
- •2. Область существования режима сложной электрической системы в пространстве активных мощностей
- •2.1. Основные положения
- •2.2. Оценка области существования режима
- •2.3. Условия односвязности множества режимов электрической системы в пространстве активных мощностей
- •2.4. Примеры неодносвязных областей существования режима
- •3. Область существования режимов в пространстве реактивных мощностей при постоянных эдс узлов
- •4. Структура области существования режима в пространстве полных мощностей
- •4.1. Уравнения установившихся режимов системы, методы их исследования
- •4.2. Качественное исследование структуры области
- •4.3. Выделение областей существования режима в пространстве полных мощностей
- •4.4. Оценки наибольших и наименьших значений линейных комбинаций мощностей. Построение многогранников, содержащих область существования режима
- •5. Предельные режимы электрических систем и их связь с конфигурацией электрической сети
- •5.1. Фазовые соотношения и пропускные способности элементов сети
- •5.2. Простейшие (понятия из теории графов
- •5.3. Заполняемые сети и графы. Задача анализа структуры
- •5.4. Анализ простейших схем
- •5.5. Замкнутые сети
- •5.6, Контуры нечетной длины и пропускные способности
- •5.7. Повышение пропускных способностей сетей, содержащих контуры* с нечетным числом ветвей
- •Дубровин б. А., Новиков с. П., Фоменко а. Т. Современная геометрия.—м.: Наука, 1979 —760 с.
5.5. Замкнутые сети
Пусть между двумя узлами сети a1 и а2 существуют два пути (µ1 µ2), несовпадающие целиком; в первом .пути т1 ветвей, во втором — m2. Обозначим т1+ число ветвей, проходимых в первом пути в положительном направлении, m1- — число ветвей, проходимых в первом пути в отрицательном направлении. Соответственно обозначим и т1+ и m1-
Предположим, что рассматриваемая сеть — заполняемая, и рассмотрим режим, при котором реализуются максимальные потоки мощности по каждой из ветвей. Тогда разность фаз в смежных узлах равна π/2. Посчитаем разность фаз для узлов а1 и а2. Вдоль первого пути φа2—φа1 = т1+ π/2 - m1- π/2=( т1+ - m1-)π/2, для второго пути та же разност фаз: φа2—φа1 = (т2+ - m2-)π/2
Сопоставляя полученное, имеем
т1+ - m1- = т2+ - m2-
Пусть т2+ = т1+ + k , где k — целое число.
Тогда из предыдущего получим m2- = m1- +k
Таким образом, для различных путей разность между числом ветвей, проходимых в положительном и отрицательном направлениях, в заполняемых графах одинакова. Из этого следует основное свойство замкнутых заполняемых сетей.
Теорема 5.2. Любой контур замкнутой заполняемой сети состоит из четного числа ветвей.
Доказательство. Рассмотрим произвольный контур и выделим в нем два различных узла: а1 и а2. Контур можно составить двумя различными путями от а1 к а2. Число ветвей в первом пути равно т1+ + m1-, во втором - т2+ + m2- . Но, как показано выше, т2+ = т1+ + k; m2- = m1- +k. Тогда общее число ветвей в контуре равно
m2 + m1 = m1+ + m1- + m1+ +k+m1- +k= (m1+ + m1- +k)*2 , т. е. четное число.
Пусть теперь на графе введена ориентация. При этом обход ветвей графа в направлении, противоположном ориентации, невозможен.
В неориентированном графе, конечно, предполагается возможность существования контуров. Однако, если граф заполняемый и ориентация его ветвей задана в соответствии с распределением мощностей, отвечающем режиму заполнения, то обход какого-либо контура в направлении, согласованном с ориентацией ветвей, невозможен. Это положение сформулируем в виде теоремы.
Теорема 5.3. В орграфе, соответствующем заполняемой сети, не существует замкнутых контуров
Доказательство. Рассмотрим какой-нибудь контур в неориентированном графе сети. Предположим, что режим заполнения дает такую ориентацию ветвей этого контура, при которой .возможен его полный обход в положительном (направлении. Выделим какую-нибудь вершину этого графа а и обозначим фазу вектора напряжения этой вершины φа. Будем последовательно обходить в положительном направлении этот контур; на каждой ветви в режиме заполнения фаза уменьшается на π/2 . Если в контуре k ветвей, то после обхода получим
φа=φа -k · π/2
откуда получаем k=0, т. е. предположение о том, что существует такой контур, неверно. Теорема доказана.
Последняя теорема дает основание для (Преобразования замкнутых заполняемых сетей к сетям, имеющим вид дерева (т. е. сетям без контуров) — преобразования, позволяющего проводить анализ режимов заполнения в схемах без контуров. Однако, прежде чем перейти к изложению правил таких преобразований, рассмотрим различные замкнутые сети, удовлетворяющие условию заполнения.
Классификация контуров в заполняемых графах
Как показано выше, в заполняемых графах возможны лишь контуры четной длины, т. е. содержащие 2, 4, 6, 8 и т. д. ветвей.
Контуры длины 2. Вообще возможны два таких контура (рис. 5.7,а, б) с различными ориентациями дуг. Однако контур, представленный на рис. 5.7,6, не может принадлежать заполняемому графу по соображениям, изложенным в доказательстве теоремы 5 3. Таким образом, контур длины 2 может быть лишь одного вида, где между узлами обе параллельные ветви ориентированы одинаково. Это -по существу одна ветвь с пропускной способностью, равной сумме пропускных способностей параллельных ветвей.
Контуры длины 4. Если рассматривать контуры с точностью до вращенияI на плоскости, то можно считать, что левая ветвь, исходящая из верхнего узла, направлена вниз. Для остальных дуг тогда имеем в общем случае ,по два различных направления. Следовательно, всего возможны 23=8 видов контуров длины 4 (рис. 5.8).

Каждый из 8 контуров проверим по правилу: сумма приращений фаз вдоль контура должна быть равна нулю. Этому условию удовлетворяют лишь 4, 6, и 7-й контуры. Но, «как легко заметить, 4-й и 7-й контуры изоморфны (поворотом на 90° один переводится в другой). Таким образом, заполняемых контуров длийы 4 может быть .всего два. На рис. 5.9 показаны эти контуры, а также указано распределение фаз в узлах в режиме заполнения.
Узлы, для которых фазы оказываются одинаковыми, можно склеить, тогда получим графы, не содержащие контуров (рис. 5.10).

Контуры длины 6. С точностью до поворота на плоскости контур длины 6 можно расположить так, что верхний узел будет смежен с ветвями, имеющими противоположные направления (такой узел всегда существует в заполняемом контуре, иначе все ветви ориентированы в одном направлении, что невозможно).
Для выбора ориентации оставшихся четырех ветвей имеется в общем случае 24=16 различных вариантов. Однако не все эти варианты будут соответствовать заполняемому графу.
Чтобы
обход «по контуру давал нулевое приращение
фазы, необходимо, чтобы 2 из 4 ветвей были
ориентированы по часовой стрелке, а
другие
2 —
'против нее. Таким образом, получаем
всего возможных вариантов: число
сочетаний из четырех по два C42=
 =6.
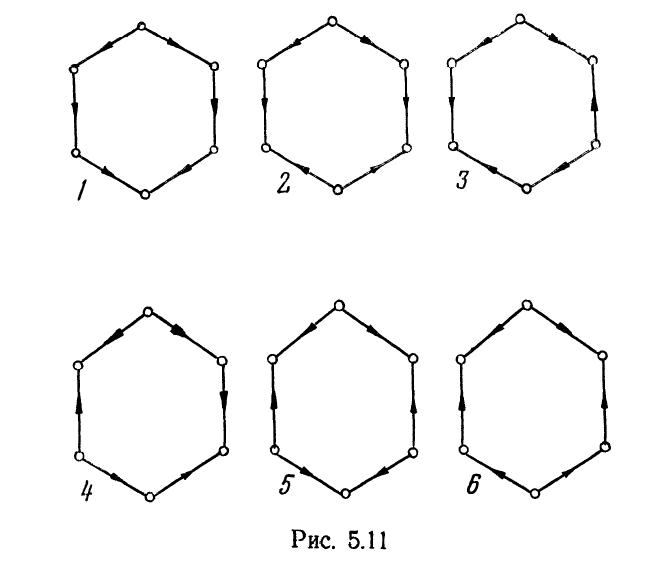
Эти 6 вариантов показаны на рис. 5.11.
Из этих 6 графов изоморфны между собой
графы 2 и 6 (переводятся друг в друга
поворотом на 180°) и графы 3 и 4 (переводятся
друг в друга поворотом па 120°). Итак,
существуют всего 4 неизоморфных
заполняемых контура длины 6; они
приведены на рис. 5.12, где указано и
распределение фаз на узлах контуров.
Склеивая узлы с одинаковыми фазами,
получим графы, указанные на рис. 5.13.
=6.
Эти 6 вариантов показаны на рис. 5.11.
Из этих 6 графов изоморфны между собой
графы 2 и 6 (переводятся друг в друга
поворотом на 180°) и графы 3 и 4 (переводятся
друг в друга поворотом па 120°). Итак,
существуют всего 4 неизоморфных
заполняемых контура длины 6; они
приведены на рис. 5.12, где указано и
распределение фаз на узлах контуров.
Склеивая узлы с одинаковыми фазами,
получим графы, указанные на рис. 5.13.
Рис.
5.12
Рис.
5.13
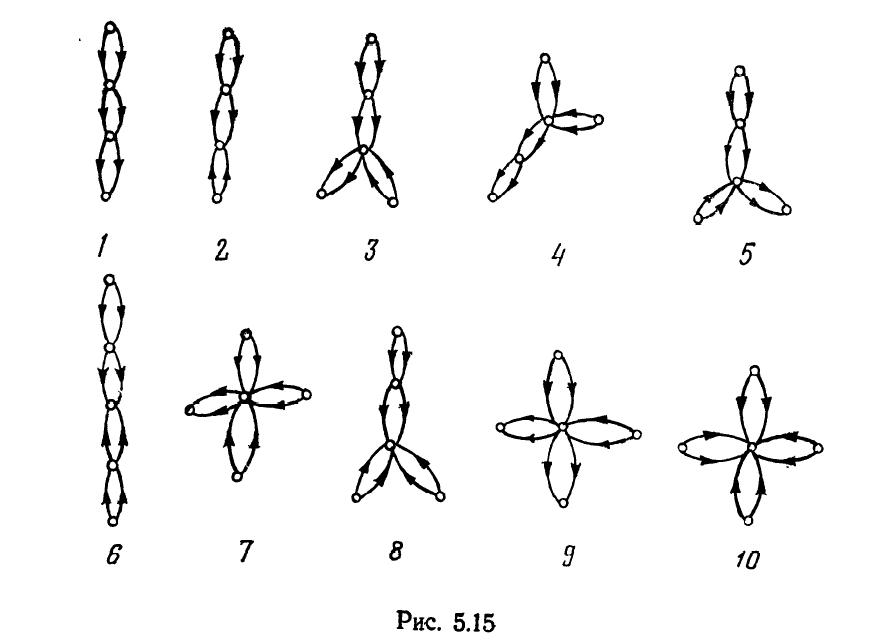
Аналогично можно рассмотреть и контуры длины 8. На рис. 5.14 приведены различные виды таких контуров, но в силу громоздкости полного анализа их здесь не приводится (на рис. 5.15 показаны склейки заполняемых контуров длины 8). Вместо этого, докажем следующую теорему, дающую хорошее средство анализа контуров в заполняемых графах.

Теорема 5.4. О склеивании заполняемых контуров. Если контур четной длины ориентирован как заполняемый граф, а его пропускные способности удовлетворяют условию заполняемости, то склеиванием вершин с совпадающими фазами векторов напряжений он может быть превращен в древовидный граф с сохранением суммарных пропускных способностей.
Доказательство. Выше было показано, что указанные в формулировке преобразования могут быть осуществлены для контуров длины 2, 4 и 6. Для доказательства сформулированного утверждения используем метод полной математической индукции.
Предположим, что это утверждение справедливо для контуров длины 2 (k—1). Рассмотрим контур длины 2k. Поскольку суммарное приращение фазы на контуре равно нулю, то ровно k ветвей этого контура ориентировано по часовой стрелке, а остальные — k ветвей — против нее. Следовательно, есть одна вершина, в которой смежные ей ветви ориентированы в противоположном направлении (в действительности таких вершин не менее двух) (.рис. 5.16,а).

Положим фазу вектора напряжения в этой вершине равной нулю, тогда в двух смежных вершинах фазы вектора напряжения в режиме передачи мощности, равной пропускной способности ветвей, равны либо π/2, либо –π/2. Поэтому в указанном выше смысле эти смежные вершины можно склеить. Получим граф, представленный на рис. 5.16,б, имеющий вид 2 (k—1)-угольника с прикрепленной к одной из вершин ветвью (двойной). Но при такой операции оставшийся граф останется заполняемым. По предположению индукции 2(k—1)-угольник можно преобразовать склеиванием вершин в дерево. Приклеивание к дереву одной ветви в любой точке не приводит к образованию контура. Таким образом, и весь граф, полученный в результате рассмотренного преобразования, будет деревом. Теорема доказана.
Рассмотренные преобразования позволяют перейти к анализу и сложнозамкнутых сетей, т. е. сетей, содержащих несколько контуров. Однако это выходит за рамки данного пособия.
