5.4. Анализ простейших схем

Действительно, для двухузловой схемы сети (один гене­рирующий и один нагрузочный узлы) ответ очевиден. Такая сеть заполняемая. Режим заполнения соответствует мощно­сти нагрузки, равной пропускной способности связи между узлами (рис. 5.1,а). Аналогично решается вопрос о сети ви­да, показанного на рис. 5.1,6. Эта сеть заполняемая, если пропускные способности дуг (а_ь а₂), (а₂, а₃), (а₃, а₄) обра­зуют строго монотонно убывающую последовательность.

Сложнее обстоит дело с сетью, указанной на рис. 5.1,6, где условия заполняемости принимают вид

S(a_u a₂)>S(a₂, a₃)+S(a_2y а₅),

S{a_b at)>S{Ob ад* $(<h, a§) >S(a_s, fle).

В этом примере уже видно, что соотношения на пропуск­ные способности непосредственно связаны с видом отображе­ния Г.

Если отображение Г построено, то

ГЯ1=02, Г02=ф8, а₅}, Газ=а₄, Га₅=а₆

г н

а) ^

Qi Qz Яз fy

г~т

и по виду множеств, составляющих Га/, записываются при­веденные выше неравенства: если

Га*«{о,ь ^ r~^lOi=a_h

то

S(a,a,)C>«S(a.. a_fl)+5(a„ а_г2)+ ... +S(a_t, а*). Эта формула дает условие заполняемое™ сети, имеющей один источник энергии и не содержащей контуров. Отобра­жение Г строится иутем перехода от генерирующего узла к ближайшему нагрузочному.

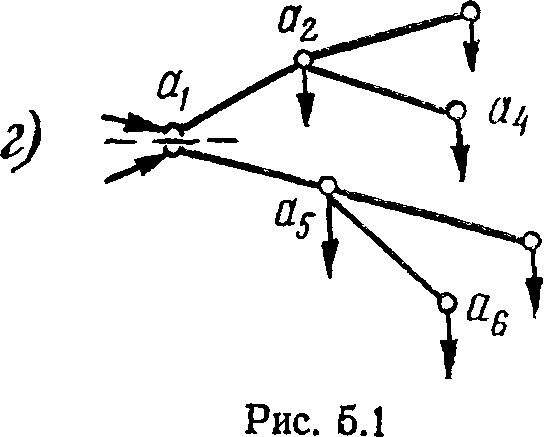
Если в сети, содержащей один 'генерирующий узел, от ге­нерирующего узла отходят две (или более) ветви, то такую сеть можно упростить, разрезав ее по генерирующему узлу на две несвязные, каждая со своим генерирующим узлом (рис. 5.1,г).

Итак, для сетей с одним генерирующим узлом, не содер­жащих контуров, задача решается элементарным образом. Введение отображения Г помогает записи соотношений в аналитическом виде.

В рассмотренных 'примерах легко увидеть и физический смысл, техническое значение понятия заполняемости и не- заполняемости. Действительно, если для сети, указанной на рис. 5.1,6, пропускная способность дуги (а₂, аз) больше про­пускной способности дуги (а_ь а₂), то эта сетынезаполняемая, пропускная способность дуги (а₂, аз) не может быть исполь­зована, поскольку ограничения по условию существования режима наступают раньше на дуге (а_ь а₂), где ори любых нагрузках, отличных от нуля, поток мощности больше, а про­пускная способность меньше.

Рассмотрим сеть, содержащую два генерирующих узла и не имеющую замкнутых контуров. Между генерирующими узлами а_гЬ а_г2 при этом существует ровно один путь. Все на­грузочные узлы вдоль это/го пути последовательно, начиная от а_гj, пронумеруем:

Пусть к узлу а_и\ подходит более двух ветвей. Для ветвей, примыкающих к этому узлу, которые не принадлежат пути между a_ri и а_г2, можно выбрать ориентацию от узла а_я\. Сог­ласованно с ней должны быть выбраны направления на всех других ветвях, следующих от ориентированной. Подграф G_auU примыкающий по этой ветви <к узлу а_нь может быть рассмотрен теперь отдельно как граф с одним генерирующим узлом, совмещенным с а_нь Аналогично могут быть рассмот­рены все остальные нагрузочные узлы: а_н2, а_аз, ..., а_нт.

Для подграфов G_aHb G_aH2, G_aHm должны быть опреде­лены суммарные пропускные способности всех ветвей, при­мыкающих к узлам а_нь а_н2, a_Hm.

Обозначим их

Рассмотрим последовательность пропускных способностей

вЬ _н2,..., S_{Hm г2}.

Теорема 5.1. Необходимое условие заполняемости сети. Если рассматриваемая сеть заполняема, то существует i (2^/^m—1), такое, что последовательности

S_T1 н1>5_н1 н2 ••• l^^Ht—1 нг,

^ г2 нт > ... ^"^Ht+l нг (5.2)

строго монотонно убывают. В противном случае сеть неза- полняемая. Доказательство очевидно из рис. 5.2, где в узле а_аг указана точка раздела потоков мощностей. Пусть выпол-

й_н1

^ап ^ам ^ам W ^антт\

1—?—Г"Т~

Рис 5.2

нено необходимое условие заполняемости. Тогда существует целое f, 'при котором выполняются условия (5.2). Теперь лег­ко сформулировать необходимые и достаточные условия.

Для тот, чтобы сеть была заполняемой, необходимо и до­статочно, чтобы для —2

5_гЬн1>5_н12:+5НЬ2, 5_нЬн2>5_н22+5_н2,НЗ,

PlMC 5.3

Рассмотрим сеть с тремя генерирующими узлами а_гЬ а_г2, а_г3, не содержащую контуров. Между узлами а_гЬ а_г2 выде­лим путь (он единственный), а также выделим путь от узла а_г3 до одного из узлов уже выделенного пути между а_т\ и а_г2. Получили трехлучевую звезду (рис. 5.3). Все остальные вет­ви графа сети можно снять: они соответствуют связям с на­грузочными узлами, питающимися от узлов звезды. Опреде­ление отображения Г для таких снимаемых ветвей очевидно. Наша задача: определить отображение Г для выделенной звезды. Г_а1 Г_а2, Г_аз очевидны, т. е. стрелки на графе должны быть направлены от генерирующих узлов.

Возможны следующие случаи положения точки раздела мощностей в такой сети:

1. точка раздела мощностей совпадает с центром звезды;

2. точка раздела мощностей принадлежит одному из лу­чей звезды.

В первом случае (рис. 5.4) пропускные способности всех элементов лучей должны монотонно убывать, кроме того в

Рис. 5.4

Рис. 5.5

каждом нагрузочном узле должно соблюдаться условие: S_нi-1,i>S_нiΣ+S_нi,+1 которое обеспечивает заполняемость под­графов сети, примыкающих к этому узлу.

Во втором случае (рис. 5.5) изложенное условие должно быть выполнено для всех лучей, за исключением того, на ко­тором находится точка раздела мощностей,

На луче с точкой раздела пропускные способности убы­вают до точки раздела как от начала луча, так и от центра звезды.

Дополнительно появляются условия, накладываемые на центр звезды:

ΣS(a_k, a_s) >S_HSΣ+5(a_s, a_k,),

где a_s — центр звезды;

a_k — узлы, смежные с центром звезды;

a_k, — узел, смежный с центром, принадлежащий лучу, на

котором находится точка потокораздела. Эти соотношения справедливы и для любого числа гене­рирующих узлов, если граф сети имеет вид многолучевой звезды (рис. 5.6).

Рис. 5 8

Таким образом, для графов, имеющих вид дерева, легко строится отображение Г и выписываются условия заполняе­мое™ сети.

Можно рассмотреть и более сложные случаи. Принципи­ально новые соотношения возникают для сетей, имеющих замкнутые контуры.