Трехклассовая классификация экосистем с точки зрения управления

К сожалению, строгой теории, описывающей функционирование иерархических систем, в настоящее время еще нет. Одной из первых и, безусловно, интересных попыток математической формализации многоуровневых иерархических систем является книга, написанная в соавторстве тремя исследователями: И. Месаровичем, Д. Мако, И. Такахарой (1973).

Условно все существующие системы разделяются на три класса:

1. одноуровневые одноцелевые системы,

2. одноуровневые многоцелевые системы,

3. многоуровневые многоцелевые системы.

На рисунке 2.2 приведена блок-схема двухуровневой многоцелевой иерархической системы.

Существующий в настоящее время математический аппарат с успехом применяется для решения задач первого класса. Ситуация в первом классе задач упрощается в виду отсутствия конфликтов внутри системы и наличия четко определенной единой цели системы. Современная теория автоматического управления является концептуальной основой для решения задач этого масса.

Существует много математических методов, которые могут быть использованы при управлении природными экосистемами, рассмотренными как одноуровневые и одноцелевые.

Применение того или иного метода зависит от постановки задачи, структуры природной или антропогенной экосистемы и от ограничений, накладываемых на экосистему. Очень часто рассматривается динамика природной экосистемы, когда некоторая величина Y является функцией переменных : .

Требуется найти такие значения , когда Y принимает максимальное значение. При этом никаких ограничивающих условий на задачу не ставится.

При такой постановке задачи максимальное значение величины Y находится из решения системы алгебраических уравнений:

(2.9)

При большом количестве для решения потребуется применение ЭВМ.

Задача становится более сложной, если появляется возможность управлять хотя бы некоторыми из переменных . В этом случае уже накладываются определенные ограничения на рассматриваемую систему.

Целый ряд задач управления

(2.10)

связан с ограничениями на систему следующего типа:

(2.11)

где k<n

В этом случае мы видим, что ограничивающие условия жестко связаны между собой. Как и прежде, требуется найти максимальное значение величины Y.

Наиболее часто встречаемая на практике задача управления ставится следующим образом: некоторая функция Y зависит от переменных :

(2.12)

При этом требуется найти максимальное значение величины

(2.13)

если переменные связаны следующими ограничениями

(2.14)

…………………………………… . (2.15)

Решением такого рода задач занимается линейное программирование.

Этот метод можно встретить в задачах, связанных с экономическими расчетами. Примером может служить задача, имеющая экономико - географическое содержание. Пусть имеются некоторые пункты , которые производят продукт, объем которого равен . Пусть пункты нуждаются в этом продукте, объем потребностей при этом равен . Обозначим через стоимость транспортировки единицы продукта из пункта в пункт , а через обозначим объем перевозок из пункта в пункт . Требуется обеспечить перевозку продукта при минимальных транспортных издержках. Математически данная задача формулируется следующим образом. Найти минимум величины (суммарной стоимости перевозок)

(2.16)

при ограничениях:

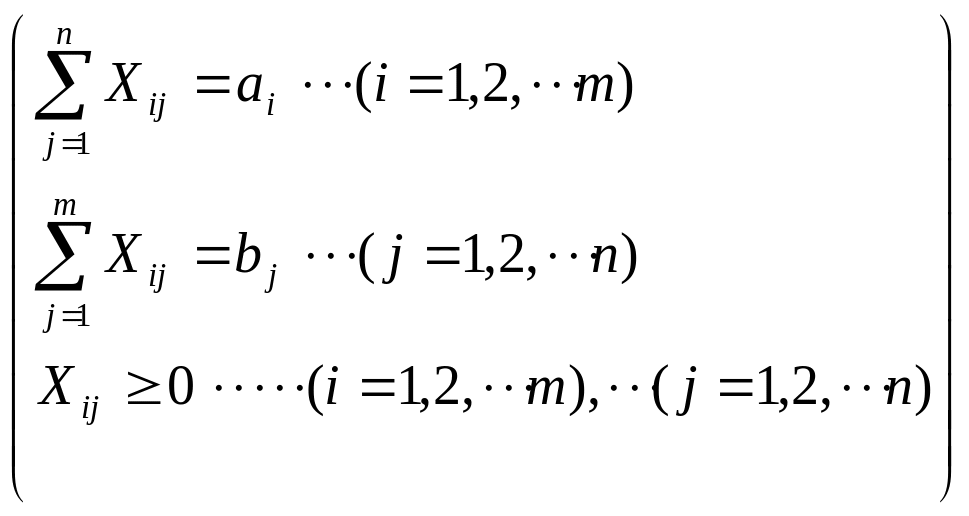(2.17)

Метод решения таких задач разработан (метод линейного программирования) и может быть активно применен географами и экологами в разных областях исследования.

В рассмотренных выше математических методах управления переменные величины были независимы от времени, т.е. процесс был стационарным. Рассмотрим теперь метод, который учитывает, что система динамическая, т.е., компоненты системы изменяются во времени.

Математическая теория управления оформилась лишь в пятидесятые годы прошлого столетия. В центр этой теории были поставлены две идеи: идея обратной связи и идея оптимизации. Обе идеи тесно контактируют с понятием «цель» функционирования системы. Существующее расхождение между получаемой и желаемой траекторией в фазовом пространстве в виде «ошибки» или «рассогласования» путем обратной отрицательной связи подается на вход системы и влияет на ее дальнейшую динамику .Управление динамической системой происходит в конце каждого из последовательных интервалов времени, в которых переменные системы имеют различные значения. Как и прежде, требуется найти максимум функции Y, являющейся переменной от величин . Если число переменных М, и каждая из M переменных может принимать L значений на каждом из N интервалов, то для нахождения максимального значения величины надо будет опробовать значений переменных. Если L, скажем, равно 5, М равно 10 и N равно 100, что вполне реально, то число переменных, для каждой из которых надо найти значение Y, равно . В этом случае даже использование ЭВМ весьма затруднительно. Возникает так называемое «проклятие размерности».

Выход из положения был предложен Беллманом (I960). В основу метода Беллмана вошли две идеи:

1) процесс считался марковским, т_.е., конечный итог после принятия i - го решения зависит лишь от i + 1 и последующих решений,

2) использовался принцип оптимальности, т.е., предполагалось, что последующие решения (после i - го решения) определяют оптимальную стратегию относительно состояния, полученного в результате i - го решения. Это означает, что если можно найти оптимальное решение на i-oм шаге, то, значит, можно найти также оптимальное решение на i + 1 шаге и на всем отрезке. Полученный метод получил название метода динамического программирования. Данный метод дал возможность намного уменьшить количество вычислительных операций для нахождения оптимального решения.

Для эффективного управления любой системы необходимо ввести критерии качества управления. Все динамические характеристики системы будут зависеть от выбранного критерия качества. Критерий качества помогает сравнивать возможные реализация процесса и выделять оптимальный процесс (т.е., наилучший в определенном смысле при наличии имеющихся ограничений в системе). При этом отыскиваются экстремальные значения данного критерия качества. Отметим, что человек на интуитивном уровне управляет сложными процессами далеко не лучшим образом, так как не успевает перерабатывать огромное количество информации.

Принцип максимума, разработанного Л.С. Понтрягиным и его учениками (Математическая теория.,..1976), был положен в основу другой идеи для оптимального управления. С помощью этого принципа был разрешен целый ряд неклассических задач. Оптимальным свойством разработанного метода явилось кусочно - непрерывное управление на определенных отрезках и скачкообразное изменение функции в определенные моменты времени.

Раскроем вкратце суть оптимального управления по Понтрягину и рассмотрим применение этого метода на примере управления некоторыми компонентами экосистемы.

Пусть имеется модель сложной динамической системы в виде дифференциальных уравнений. Будем считать, что существует n действительных переменных, которыми можно управлять. Предположим, что между управляющими параметрами существует некоторая зависимость:

Каждый из управляющих параметров является функцией времени и определен на отрезке времени .

В определенные моменты времени возможен скачок функций .Однако на участках функции непрерывны. Для нахождения полного решения управления динамической системой отыскивается сначала управление и решение на тех отрезках времени, когда функции - непрерывна, а затем «сшиваются» полученные решения. Таким образом, практически осуществляют перевод из одной точки фазового пространства в другую. Если нет никаких ограничений в системе, то такой перевод можно осуществить различными способами. Для того, чтобы получить единственное решение, вводят оценочную функцию (критерий качества) в виде функционала:

(2.18),

который зависит как от решения, так и от управления системой. Управления должны быть такими, чтобы было получено экстремальное значение этого функционала. Естественно, что в зависимости от выбранного функционала в результате решения будут получены те или иные реализации процесса. Реализации процесса сильно зависят также от интервала времени, на котором отыскивается максимальное значение функционала. Если созданы математические модели природных экосистем или их элементов, то можно ставить задачи оптимального воздействия на эти системы.