Применение теории игр для выбора стратегий в области сельскохозяйственной политики

Предположим, что имеется сельскохозяйственное предприятие, которое выращивает две культуры: . Конечный результат (урожай) зависит от погодных условий. Цель исследования - дать рекомендации, какие культуры и в каких количествах следует сеять, если их урожаи зависят от погоды, а план посева должен обеспечить наибольший доход для сельскохозяйственного предприятия . (Целесообразно иметь в виду, что большая часть России находится в зоне рискованного земледелия).

Проанализируем данную ситуацию с позиции теории игр (Шикин, 2003). Игрок А (человек) имеет четко выраженную цель - получить максимальный урожай. У игрока В (природа) нет явно выраженной цели, но, в зависимости от ситуации, он может сильно навредить игроку А. Итак, у игрока А имеется две стратегии: стратегия - посев первой сельскохозяйственной культуры и стратегия - посев второй сельскохозяйственной культуры. У игрока В имеется три стратегии: стратегия - засушливое лето, стратегия - лето с обычным количеством осадков, стратегия - лето с сильно избыточным количеством осадков.

Для решения задачи следует составить матрицу, где указаны расчетные варианты урожаев для сценарных вариантов погодных условий (условно, в млн. рублей).

(2.24)

В полученной матрице отсутствует седловая точка. Поэтому решение задачи надо искать в области смешанных стратегий:

(2.25)

Цена игры равна 4.

Физически данное решение означает, что на 60 % территории следует применить стратегию (т.е., выращивать первую культуру), а на 40 % территории следует применить стратегию (т.е., выращивать вторую культуру). При этом общий урожай будет не менее 4 млн. рублей (цена игры). Таков результат (урожай) при худших погодных условиях. Если погодные условия будут лучше, то и урожай будет больше.

Применение теории игр к строительству противолавинных сооружений.

Второй пример связан со строительством противолавинных сооружений.

Использование горной территории в рекреационных целях всегда связано с проблемой защиты от лавин и селей: зданий, канатных дорог, используемых для катания склонов, а также проживающих в этих районах жителей и горнолыжников, катающихся по данным склонам. В целях безопасности часто требуется строительство противолавинных сооружений, а для этого нужны значительные материальные затраты. Именно поэтому необходимо создание карт лавинной опасности территории, связанной с рекреационной деятельностью. Карты лавинной опасности помогают прояснить в целом лавинную ситуацию района. Одной из задач для составления карт является оценка объема снега, который может быть потенциально вовлечен в движение и, в результате, принести материальный ущерб.

Предположим теперь, что карты лавинной опасности имеются и на них отмечены участки, подвергающиеся лавинной опасности один раз во много лет. Проанализируем данную ситуацию. Если организация, которая контролирует данную ситуацию, располагает большим количеством материальных средств, то никакой научной задачи не возникает. Можно построить (с избытком) на всех склонах противолавинные сооружения, создать рекламу о безопасности катания на данных склонах в виду наличия противолавинных сооружений и получать соответствующую ситуации выгоду. Проблема возникает (а это более реальная жизненная ситуация), когда имеется ограниченное количество материальных средств. Стоит ли создавать на всех участках противолавинные сооружения при ограниченном количестве материальных средств? Какие выбрать участки? Такая задача может быть отнесена к области конфликтных ситуаций, и аппарат теории игр может помочь наилучшим образом распределить имеющиеся материальные средства для создания противолавинных сооружений.

Проанализируем данную задачу. Пусть на территории, подвергающейся сходу лавин, имеются лавиноопасные склоны, по которым с определенными частотами движутся лавины (или сели, или то и другое вместе) в разное время в течение года. Сход лавин приносит определенный материальный ущерб и порой угрожает здоровью и даже создает угрозу жизни людей. Требуется создать противолавинные сооружения, с учетом того, что количество средств, отпущенных на создание этих противолавинных сооружений, ограничено суммой М. Как наиболее оптимально распределить эти средства? Данная задача относится к области конфликтных ситуаций, и конечный результат зависит от конкретных действий каждой из сторон. В одном случае при этом подразумеваются действия человека, в другом - природы.

Рассматривая строительство противолавинных сооружений, мы имеем дело с игрой m* n. Это означает, что природа имеет m стратегий (лавиноопасных склонов), а человек имеет n стратегий (в частности, он может построить на склоне противолавинное (одно или несколько) сооружение). Данная игра содержит случайные ходы, так как мы не знаем точно время, когда сойдет лавина.

Для решения задачи в области смешанных стратегий введем - относительные частоты применения стратегий и запишем следующую систему уравнений:

(2.26)

Разделим левые части уравнения (2.26) нa q и введем обозначения:

(2.27)

Перепишем уравнение (2.27) в следующем виде:

(2.28)

Так как желание человека заключается в увеличении выигрыша, следовательно:

должна быть минимальной. Для решения такого рода задачи разработан математический аппарат линейного программирования. Решение уравнений (2.28) дает возможность вычислять цену игры q.

Перераспределяя различными способами сумму М, отпущенную на строительство противолавинных сооружений, человек изменяет коэффициенты матрицы.

Вычисляя в каждом конкретном случае цену игры q, можно найти оптимальный вариант, который дает возможность распределить средства таким образом, чтобы выигрыш со стороны человека был максимален.

Рассмотрим в качестве иллюстрирующего примера два лавиноопасных склона, по которым спускаются лавины мощностями . Будем считать, что ущерб, производимый лавиной, прямо пропорционален ее мощности и равен: . (Коэффициенты получены путем перемножения мощностей лавин на вероятности их схода . Для расчета использовались следующие значения: , ).

Предположим, что суммы противолавинных средств М, имеющейся в наличии, хватает ровно для того, чтобы создать противолавинные сооружения, преграждающие путь лавине мощностью . Допустим, что 50% средств М достаточно для полной защиты от лавины мощностью . Рассмотрим три варианта (три стратегии) со стороны человека. При первой стратегии ( ) все средства М тратятся на преграждение пути лавины мощностью , при этом вторая лавина может двигаться беспрепятственно. Суть второй стратегии ( ) в следующем: средства делятся пополам для создания противолавинных сооружений первой и второй лавин. При этом вторая лавина будет полностью закрыта. Согласно третьей стратегии ( ) все средства тратятся на создание сооружения для второй лавины. Матрица игры будет иметь следующий вид:

(2.29)

Так как каждый элемент стратегии больше или равен элементу стратегии , то стратегия заведомо невыгодная, и ее можно вычеркнуть. Решая систему уравнений, содержащую две стратегии человека ( ):

(2.30)

найдем

Данное решение означает следующее: для получения выигрыша надо в 29 % пользоваться стратегией , а в 71 % стратегией .

Конечно, сход лавин – явление вероятностное, тем не менее, в данном случае вторая стратегия явно предпочтительнее.

Многоуровневые иерархические многоцелевые системы.

К третьему классу задач относятся многоуровневые иерархические многоцелевые системы.

Примером многоуровневой иерархической многоцелевой системы является любое государство. Московский государственный университет имени М.В. Ломоносова , состоящий из факультетов и сами факультеты представляют собой также многоуровневые иерархические многоцелевые системы.

В многоуровневых иерархических многоцелевых системах подразумевается, что:

1) система состоит из четко выделенных взаимодействующих подсистем, имеющих вертикальную соподчиненность,

2. по меньшей мере, некоторые из подсистем являются принимающими решение,

3. принимающие решения подсистемы могут управляться другими подсистемами, т.е., наблюдается иерархия подсистем.

Указанная выше книга (Месарович и др., 1973) представляет собой попытку построения математической теории иерархических многоуровневых многоцелевых систем.

Рассматриваемая теория характеризуется тремя важнейшими направлениями:

1. вводится понятие организации и иерархическая структура составляющих ее систем считается важнейшей характеристикой организации,

2. участник, от которого зависит решение, рассматривается как часть организации, т.е., он описывается как одна из ее систем,

3. важнейшей функцией всей организации в целом считается ее способность координировать взаимную связь подсистем, которые принимают решение.

Координация представляет собой проблему принятия решения системой верхнего уровня. При принятии решения должно быть оказано воздействие на нижестоящие уровни таким образом, чтобы была достигнута конечная цель, стоящая перед организацией в целом. Следует отметить специфику и коренное отличие третьего класса систем от двух предыдущих. Природные экосистемы (а также антропогенные экосистемы, где принятие решений носит социальный характер), как правило, относятся к третьему классу систем. И если к решению конкретных задач третьего класса пытаются применять идеи и методы, разработанные для первых двух классов, то это связано, в первую очередь, с недостаточной разработкой (имеются в виду методологические трудности определения понятия целей для природных экосистем, а также проведение конкретных расчетов) теории иерархических сложных многоуровневых многоцелевых систем.

Системы третьего класса - информативные системы. Координирующий орган принимает решение на основе информации, которую он получает от нижестоящих элементов, при этом в системе осуществляется отрицательная и положительная обратная связь. Но кибернетическая идея обратных связей господствует во всех трех классах. Принципиальное отличие систем третьего класса от двух первых заключается в том, что элементы высшего уровня не жестко управляют поведением элементов нижних уровней, а лишь координируют их деятельность.

Поясним данную мысль. Если вышестоящий элемент (координатор) точно знает, как функционируют все нижестоящие элементы, то в результате возникает классическая задача управления - выбор оптимального (в каком-то смысле наилучшего) режима управления. Это - первый класс систем. Отметил, что в этом классе структура систем фиксирована. В многоуровневой системе количество элементов настолько велико, что указанный подход практически невозможен для получения точных и практически важных рекомендаций. Один из подходов исследования функционирования многоуровневых систем заключается не в детальном, а в упрощенном описании работы подсистем нижних уровней. Этот подход наиболее часто применим в настоящее время. В этом случае используется метод агрегирования переменных. Результатом такого подхода является управление вышестоящего элемента относительно небольшим числом нижестоящих элементов. Классические способы теории управления так же применимы в этом случае.

Совершенно другая идея господствует при рассмотрении функционирования сложной иерархической многоуровневой многоцелевой системы. Вышестоящий элемент (координатор системы) учитывает, что нижестоящие элементы могут иметь собственные цели, которые, в принципе, могут расходиться с целями координатора. Поэтому, посылая управляющие сигналы в систему, координатор должен руководствоваться не только своей целью, а также целями нижестоящих элементов и всей целью системы. Отсюда возникает несколько специфических для теории управления проблем, в частности, проблема как разработки понятия цели всех уровней системы, так и общей цели системы, согласование целей, а также проблема устойчивости системы в целом и подсистем в частности. Здесь следует отметить, что в иерархических многоуровневых системах всегда возникает разного рода неопределенность, имеющая принципиальный характер и не связанная с точностью наблюдения и измерения. Так, в процессах, связанных с социально - экономическими проблемами, цели входящих в рассматриваемую систему уровней принципиально не могут быть точно определены в процессе моделирования. Отсюда естественно возникает проблема развития специальной теории многоуровневых иерархических систем.

Рассматривая задачи и цели многоуровневых иерархических систем, можно выделить следующие общие черты:

1) чем выше уровень исследуемой подсистемы, тем более широкие аспекты поведения системы в целом рассматриваются этим уровнем,

2) время принятия решений тем больше, чем выше уровень занимает подсистема,

3) подсистема верхнего уровня имеет дело с более медленными аспектами поведения системы,

4) чем выше уровень, тем больше неопределенности должно учитываться данной подсистемой для принятия решений.

Из всех возможных многоуровневых иерархических систем наиболее простой является система, где все элементы одного уровня подчинены одному органу высшего управления

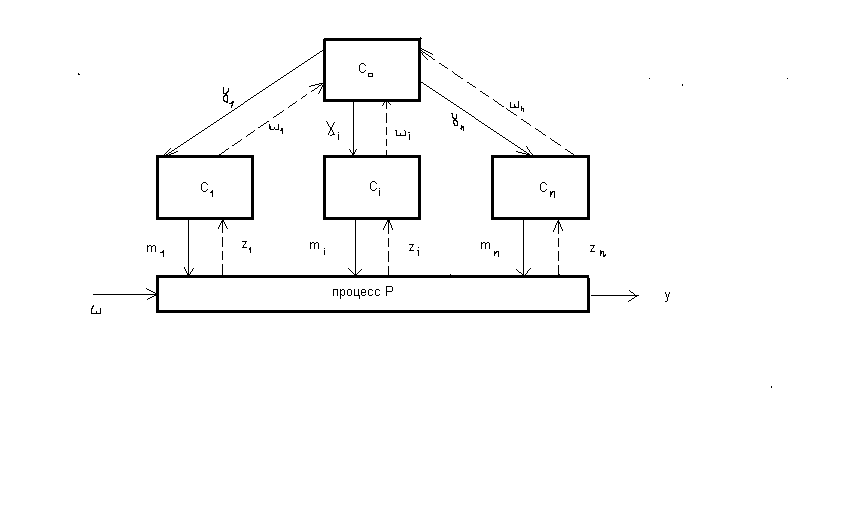
Рис. 2.2 Двухуровневая многоцелевая, иерархическая система.

Это так называемая двухуровневая многоцелевая, иерархическая система. Рассматриваемая система относительно проста и может быть использована в качестве модуля для синтеза более сложной иерархической, многоуровневой системы. Приведенная на рис. 2.2 блок - схема двухуровневой, иерархической системы состоит из n + 2 подсистем. - является единственной вышестоящей управляющей подсистемой. Далее имеются: n управляющих подсистем нижестоящего уровня и управляемый процесс Р. Данная организация представляет собой информационную систему по переработке информации для удовлетворения общей цели всей системы в целом. Процесс Р - это управляемая подсистема, на которую поступают воздействия как со стороны управляющих подсистем , так и возмущения из внешней среды. На управляющие подсистемы поступает координирующий сигнал от вышестоящей управляющей системы . Представленные на рис. 2.2 пунктирные линии отражают существующую в системе отрицательную обратную связь по передаче информационных сигналов наверх в управляющие системы. У процесса Р имеется выход у, который связан с существующей в системе общей целью. Вводится предположение, что отсутствует непосредственная связь между нижестоящими управляющими системами. Считается также, что вышестоящая система не связана непосредственно с процессом Р.

В рассматриваемой системе можно выделить три вида целей:

1. цели органов нижестоящих подсистем ,

2. цели вышестоящего органа ,

3. цель всей системы в целом (общая цель).

Часто при этом общая цель системы и цели вышестоящего органа являются различными. Для того чтобы общая цель была достигнута, вводится «постулат согласованности», который заключается в правильном выборе целей и постановке задач перед всеми управляющими подсистемами. Достижение общей цели осуществляется за счет координации деятельности подсистем, которые в какой-то мере независимы с точки зрения выбираемых ими способов действия. Каждая из нижестоящих управляющих подсистем старается действовать таким образом, чтобы достичь своих собственных целей. Поэтому может возникнуть конфликтная ситуация, которая должна быть разрешена с помощью действий вышестоящего органа (координатора). Координатор тоже преследует свои цели, поэтому он посылает координационный сигнал, руководствуясь их осуществлением. Так как непосредственно с процессом Р взаимодействуют подсистемы , то общая цель достигается тогда, когда все решаемые двухуровневой иерархической системой задачи совместимы. Совместимость всех существующих в системе целей возможна только в том случае, если решающие подсистемы обладают некоторой свободой действия в выборе своих решений. Как указывалось выше, вышестоящая подсистема (координатор) руководит работой нижестоящих подсистем , но не жестко управляет ими. Проблема заключается в выборе ограничений, которые должны быть наложены на нижестоящие подсистемы, чтобы обеспечить выполнение всех целей, стоящих перед системой.

Показано, что возможность координирования иерархической системой зависит от локальных оптимизационных задач и взаимосвязей систем между собой. Координирование такой системой возможно лишь в случае определенных связей между локальными элементами. Поэтому может возникнуть необходимость изменения локальных оптимизационных задач.

Если известна общая цель системы, то из нее локальные цели могут быть получены путем фиксации входящих в общую цель переменных. Проводимая вышестоящим элементом координация функционирования системы осуществляет две важные функции:

1. если структура системы фиксирована, то отыскивается управление, которое ведет к удовлетворению общей цели,

2. если изменение структуры системы возможно, то осуществляется управление таким образом, что в случае необходимости изменяется структура системы.

При этом основной целью координирования является нахождение таких управляющих воздействий, чтобы была достигнута общая цель системы.

Примером одноуровневой одноцелевой системы может служить популяция, развивающаяся при определенных фиксированных внешних воздействиях. Известно, что численность популяции растет по логистической кривой. Целью такой одноуровневой одноцелевой системы можно считать стремление системы достигнуть асимптотического предельного состояния, численно равного .

Система, описывающая взаимодействие нескольких популяций одного уровня, может быть отнесена к одноуровневой многоцелевой системе. Каждый элемент системы (популяция) имеет свою собственную цель, выражающуюся в стремлении достигнуть свою асимптоту. Однако взаимодействие с другими элементами системы мешает достижению этой цели. Общей целью системы является существование ее в определенных пределах, определяемых параметрами как самой системы, так и параметрами, зависящими от окружающей систему среды. При рассмотрении лишь растительного компонента примером одноуровневой многоцелевой системы может служить система взаимодействия леса и степи.

К многоуровневой многоцелевой иерархической экосистеме можно отнести пирамиду Элтона. Эта пирамида берет в основу функциональные взаимоотношения между популяциями внутри природной экосистемы на основе изучения цепей питания. Элтон отметил, что число иерархических уровней в природной экосистемы невелико. При этом вырисовывается четкая зависимость: чем выше иерархический уровень, тем меньше численность его обитателей. В результате образуется пирамида, основанием которой служат микроорганизмы и многочисленные виды растений, последующие уровни образуют растительноядные и плотоядные животные. В вершине пирамиды находятся самые крупные хищники.

Значительно труднее выделить в функционировании такой природной экосистемы цели подсистем и общую цель. Здесь можно лишь выдвинутъ рабочую гипотезу, что целью каждого организма, как и всего уровня в целом является стремление существовать в течение длительного времени.

Антропогенная экосистема также представляет собой многоуровневую, иерархическую систему. При этом самым главным хищником на вершине пирамиды является человек с его все возрастающей численностью и увеличивающимися из года в год потребностями. Отметим, что в антропогенной экосистеме понятие «цель» определяется легче, чем в природной экосистеме, так как во многом диктуется потребностями человека.