КОМПЛЕКТ ТЕСТОВЫХ ЗАДАНИЙ № 18

Дисциплина мат биолог

Количество часов 55

Тип комплекта B

Количество модулей 4

Количество вопросов 400

Дата записи в Банк Не записан

1. Берілген В(3) жєне АВ=5 бойынша А нуктесінін координатасын есептеніз:

1. 2

2. -2

3. 5

4. 1

5. 3

2. А(-1) жєне В(5) н‰ктелерімен шектелген кесіндініњ ортасыныњ координатасын аныќтањыз:

1. -3

2. 2,5

3. -1

4. 3

5. 2.

3. ху>0 шартын ќанаѓаттандыратын М(х;у) н‰ктесі ќай ширекте жатуы м‰мкін:

1. 1

2. 2,3

3. 2,4

4. 1,3

5. 1,2,3

4. А(-3 ;4) жєне В(-2;2) н‰ктелерініњ ара ќашыќтыѓын аныќтањыз:

1. 7

2. 3

3. 4

4. 5

5. 5

5. Шаршыныњ А(3;-7) жєне В(-1;4) сыбайлас екі тµбесі берілген. Шаршыныњ ауданын есептењіз:

1. 122

2. 137

3. 125

4. 25

5. 10

6. ‡шб±рыштыњ А(1;4), В(3;-9) жєне С(-5;2)тµбелері берілген. В тµбесінен ж‰ргізілген медиананыњ ±зындыѓын табыњыз:

1. 12

2. 11

3. 10

4. 13

5. 15

7. 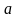(1,0,2) жєне в (3,-4,1) векторларыныњ арасындаѓы косинус б±рышын табыныз:

1.

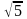
2.

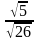
3.

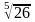
4.

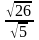
5.

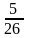
8. Зх-2у-4=0 жєне 2х-у-3=0 т‰зулерініњ ќиылысу н‰ктесі арќылы µтетін , ординат осіне параллель болатын т‰зудіњ тењдеуін табыњыз:

1. х=2,5

2. х=2;

3. х=-2

4. х=3;

5. х=2,8

9. Екі т‰зудіњ перпендикулярлыќ шарты?

1.

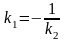
2.

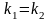
3.

4.

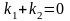
5.

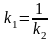
10. Зх-2у-4=0 жєне 2х-у-3=0 т‰зулерініњ ќиылысу н‰ктесі арќылы µтетін , ординат осіне параллель болатын т‰зудіњ тењдеуін табыњыз:

1. х=2,5;

2. х=2

3. х=-2

4. х=3

5. х=2,8

11. х²+у²=8, x-y=0 екі сызыќтыњ ќиылысу н‰ктесін табыњыз:

1. (1; -1), (1; 1)

2. (2; 2), (-2; -2)

3. (2; 2)

4. (-2; 2), (2;-2)

5. (-2;-2).

12. 4х-5у+2=0 т‰зуіне перпендикуляр жєне А(-1;3) н‰ктесі арќылы µтетін т‰зудіњ тењдеуін табыњыз:

1. 4х+у+5=0

2. 4х+у+6=0;

3. 4х+у-16-0

4. 4х+у+1б=0

5. 5х+4у-7=0

13. 4х-5у+2=0 т‰зуіне параллель жєне А(-1;3) н‰ктесі арќылы µтетін т‰зудіњ тењдеуін табыњыз:

1. 4х+5у+19=0

2. 4х+5у-19=0

3. -4х+5y-12=0

4. 4х-5у+19=0;

5. -4х+5у-13=0

14. А (-1 , 6) В (-3 , 4) н‰ктелері арќылы µтетін т‰зуге перпендикуляр т‰зудіњ б±рыштыќ коэффициентін табыњыз:

1. 4

2. 3

3. -1

4. 1

5. 

15. x - 5y + 4 = 0 т‰зуіне перпендикуляр болатын, т‰зудіњ б±рыштыќ коэффициентін табыњыз:

1. 6

2. -5

3. 1/5

4. -3

5. табылмайды

16. Шаршыныњ ќабырѓасыныњ тењдеуі 3x+4y+4=0, бір тµбесініњ координатасы (1;2). Шаршыныњ ауданын табыњыз:

1. 9 ш.б

2. 10 ш.б

3. 2 ш. б

4. 2,5 ш. б

5. 3 ш. б

17. ‡Шб±рыштыњ тµбелері берілген а(3, 2), в(5, -2), с(1, 0). An медиананыњ тењдеуін ќ±рыњыз:

1. у=5

2. х+3=0

3. у=0

4. х+у-3=0

5. х-3=0

18. М(2,-1) н‰ктесiнен 4x+3y+10=0 т‰зуiне дейiнгi араќашыќтыќты табыњыз:

1. 2

2. 3

3. 4

4. 5

5. 1

19. m жєне n-ніњ ќандай мєндерінде mx+8y+n=0, 2x+my-1=0 екі т‰зуі параллель болады:

1. m=2, n=4

2. m=2,n=-4;

3. m=0,n-кез келген мєн

4. m=-4, n=2 немесе m=4, n=2

5. m=-4, n?2 немесе m=4, n?-2

20. Т‰зудіњ жалпы тењдеуін аныќтањыз:

1. y=kx+b

2. y=kx;

3. y-y₀=k(x-x₀)

4. Ax+By+C=0

5. y=0

21. 2x+3y-6=0 т‰зуiнiњ кесiндiлiк тењдеуiн жазыњыз:

1.

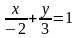
2.

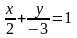
3.

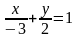
4.

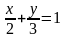
5.

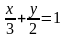
22. 3х-4у-29=0 жєне 2х+5у+19=0 екі т‰зудіњ ќиылысу н‰ктесін табыњыз:

1. (0, 5)

2. (-3, -5)

3. (3, 5)

4. (-3, 5)

5. (3, -5)

23. Ав кесіндісініњ ортасын табыныздар, егер а (-3; 5), в (5; 1)

1. (4; 3);

2. (1; 3);

3. (-1; 4);

4. (2; 3);

5. (1; 5).

24. А (1; -1) жєне В (2; -3) н‰ктелері арќылы µтетін т‰зудіњ тењдеуін табыныз.

1. у-2х+1= 0;

2. у+2х-1= 0;

3. у-2х-1= 0;

4. 2х+у+1= 0;

5. -2х-у+4= 0.

25. А (-1; 0) жєне В (2; -1) н‰ктелері арќылы µтетін т‰зудіњ тењдеуін.

1. х-3у+1= 0;

2. -х+3у+1= 0;

3. х+3у-1= 0;

4. х+3у+1= 0;

5. х-3у+2= 0.

26. 3х + 4у -5 = 0 т‰зудіњ б±рыштыќ коэффициентін табыныз.

1. ;

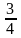2. ;

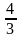3. - ;

4. - ;

5. .

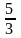27. 5х - 3у +2 = 0 тїзудіѕ бўрыштыќ коффициентін табыныз.

1.

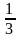
2.

3. ;

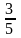4. - ;

5. .

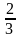28. Ќисыќтар тењдеулерімен берілген: 1) х - у + 1 = 0; 2) х² +у² = 1; 3) х² -у = 0;

4) ху + 1 = 0; 5) 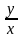= 1. Ќисыќтын ќандайы басты координаттан µтеді.

1. 1;

2. 2;

3. 3;

4. 4;

5. 5.

29. Ќисыќтар тењдеулерімен берілген: 1) х² - у + 1 = 0; 2) х² -у² = 1; 3) х +у = 0;

4) у-х +1 = 0; 5) х²+у² = 4. Ќисыќтын ќандайы басты координаттан µтеді.

1. 1;

2. 2;

3. 3;

4. 4;

5. 5

30. А (2; -5) жјне В (3; 2) н‰ктелерінен µтетін т‰зудіњ б±рыштыќ коэффициентін табыныз.

1. -3;

2. ;

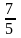3. - ;

4. 7;

5. -7.

31. А (-3; 1) жєне В (7; 8) н‰ктелерінен µтетін т‰зудіњ б±рыштыќ коэффициентін табыныз.

1. ;

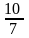2. ;

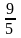3. ;

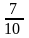4. - ;

5. .

32. 2х-у-3=0 жєне х+у-3=0 т‰зулерініњ ќиылысу нуктесіњ табу керек.

1. (-2;1);

2. (2;-1);

3. (2;1);

4. (1;1);

5. (-1;-1).

33. 2х-у-3=0 жєне х+2у-4=0 т‰зулерініњ ќиылысу нуктесіњ табу керек.

1. (-2;1);

2. (2;1);

3. (1;1);

4. (-2;-1);

5. (2;2).