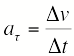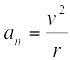1 Материальная точка - это тело, размерами которого в данной ситуации можно пренебречь. Это понятее нужно, к примеру, когда мы измеряем растояние между звездами, которые могут достигать нескольких парсеков. Не станем же мы учитывать радиус этих звезд?  Системы координат бывают подвижные и неподвижные. Однако одна система координат может быть неподвижна относительно точки отсчета, и подвижна относительно другой точки отсчета. Например:  Пассажир автобуса неподвижен относительно самого автобуса (если, конечно, просто в нем стоит), но подвижен относительно земли, причем двигаться он будет со скоростью автобуса

Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел^[2][3]. Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени tкоординаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями  ,  ,  .

Кинематическое уравнение движения точки

При движении материальной точки М ее координаты   и радиус-вектор   изменяются с течением времени t.Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:

2 Вращение вокруг неподвижной оси

Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения.         Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' (рис. 2.12).

. Тангенциальное и нормальное ускорения

В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением  . Она характеризует изменение скорости по модулю.

Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением  . Она характеризует изменение скорости по направлению.

Угловая скорость. Углова́я ско́рость — физическая величина, являющаяся псевдовектором (аксиальным вектором) и характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени:

,

3 Границы применяемости классической механики

Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, его вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «ньютоновой механикой».Классическая механика подразделяется на: статику (которая рассматривает равновесие тел);кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин);динамику (которая рассматривает движение тел с учётом вызывающих его причин).Существует несколько эквивалентных способов формального математического описания классической механики: Законы Ньютона Лагранжев формализм Гамильтонов формализм Формализм Гамильтона — Якоби

Первый закон Нь..тона Если на тело не действует внешняя сила, то тело находится в состоянии покоя или равномерного прямолинейного движения. ахаха это я тебе как физик, Викун говорю))) а формулы нету!)

2 закон Ньютона Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.  Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике. 

Третий закон НьютонаЭтот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой, а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.