Сравнение бесконечно больших функций
Также как и в предыдущем пункте будем рассматривать предел отношения двух функций. Только теперь у нас функции стремятся к бесконечности при аргументе x, стремящемся к А. Возможны следующие варианты:
1) , т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка.
2) , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка.
3) , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.
4) Если данный предел: не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.
Эквивалентные величины [править]Определение
Если 
,
то бесконечно малые
величины 
и 
называются эквивалентными (
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При 
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
22. Первый замечательный предел.
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела.
Первый замечательный предел:
Следствия
23. Второй замечательный предел. Второй замечательный предел
или 
Следствия
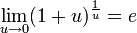
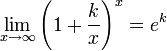
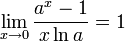для 
, 
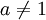
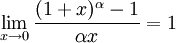
24. Понятие производной и ее геометрический смысл. Уравнение касательной и нормали к кривой.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Геометрический смысл производной.
Тангенс
угла наклона касательной (угловой
коэффициент наклона касательной),
проведенной к графику функции 
в
точке 
равен
производной функции
в
этой точке:
Заметим,
что угол 
–
это угол
между прямой и положительным направлением
оси ОХ:
Уравнение касательной к графику функции в точке имеет вид:
В этом уравнении:
– абсцисса точки касания,
–
значение
функции
в
точке касания,
–
значение
производной функции
в
точке касания.
Нормалью называется
прямая, проходящая через точку касания
перпендикулярно касательной. поэтому
ее угловой коэффициент равен 
,
а уравнение записывается в виде:
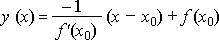
25. Основные правила дифференцирования. Логарифмическая производная.
К основным правилам дифференцирования относят:
вынесение постоянного множителя за знак производной
производная суммы, производная разности
производная произведения функций
производная частного двух функций (производная дроби)
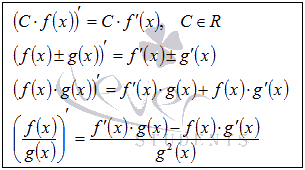
Логарифмическая произво́дная — производная от натурального логарифма функции.
Часто применяется для упрощения нахождения производной некоторых функции, например сложно-показательных.