1) Матрицы. Действия над матрицами. Обратная матрица.

Определение: Матрицей называется прямоугольная таблица чисел, содержащая m строк  и n столбцов.  Когда говорится о размерах матрицы, то сначала указывается число строк, затем число столбцов. Если количество строк и столбцов совпадает, то такая матрица называется квадратной. Матрица, состоящая из одной строки или столбца - вектор.

Действия над матрицами: 1. Внесение/вынесение минуса из матрицы (меняем знак каждого элемента матрицы). 2. Умножение матрицы на число (каждый элемент матрицы умножается на это число). 3. Транспонирование матрицы (Поворачивание набок. Первую строку записываем в первый столбец, вторую строку во второй столбец, третью в третий и т.д.) 4. Сложение/вычитание матриц. ПРИМЕНИМО ТОЛЬКО К МАТРИЦАМ ОДИНАКОВОГО РАЗМЕРА. (Для того, чтобы сложить/вычесть матрицы необходимо найти сумму/разность соответствующих элементов) 5. Умножение матриц ЧТОБЫ МАТРИЦУ    МОЖНО БЫЛО УМНОЖИТЬ НА МАТРИЦУ   НУЖНО, ЧТОБЫ ЧИСЛО СТОЛБЦОВ МАТРИЦЫ   РАВНЯЛОСЬ ЧИСЛУ СТРОК МАТРИЦЫ  . (Умножение L на K уже невозможно)

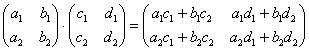  6. Нахождение обратной матрицы.

Чтобы матрица имела обратную матрицу, необходимо, чтобы её определитель не равнялся нулю.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E (Матрица, в которой все элементы равны нулю за исключением тех, что находятся на главной диагонали - они равны единице.) Это транспонированная матрица, составленная из алгебраических дополнений и деленная на определитель исходной матрицы.

2) Определители 2-го и 3-го порядков. Вычисление определителей 3-го порядка по правилам треугольника, Саррюса.

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

                      .

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

 Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка по правилам треугольника и Саррюса.

Правило треугольника: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус.

Правило Саррюса: К матрице третьего порядка необходимо дописать два первых столбца. Произведения трех первых диагоналей, сонаправленных с главной, складываются, а произведения трех диагоналей, сонаправленных с побочной, вычитаются из суммы произведений трех первых.