1. Функція корисності для опр, схильної до ризику не спадна, тому що більша кількість грошей завжди привабливіша їх меншої кількості.
2. Її графік угнутий. Це означає, что відносна корисність грошей зростає.
У цьому випадку при виграші певної суми грошей корисність зросте на більшу величину, ніж величина корисності при втраті тієї ж суми грошей.
Наприклад, якщо при початковій сумі 200 грн. ви отримаєте з певного джерела (виграєте) 100 грн., то корисність зросте на величину
U(300) - U(200) =.
Якщо ж при початковій сумі 200 грн. ви втратите (програєте) 100 грн., то корисність зменшиться на величину
U(200) - U(100) =
Таким чином, для ОПР, схильної до ризику, привабливіший виграш, ніж програш. На програш ОПР схильна до ризику звертає значно менше уваги. Для ОПР пріоритетнішим є участь у лотереї, ніж можливість одержати гарантовано сподіваний виграш. Корисність очікуваного доходу менша, ніж очікувана корисність для ОПР схильної до ризику
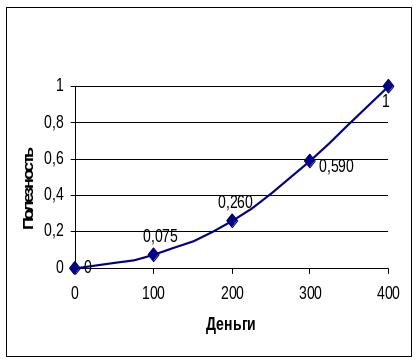
Рис. 7. Функція корисності для ОПР, схильної до ризику
Далі, ОПР Y є нейтральною(байдужою) до ризику, так як згадані зміни породжують однакові зміни корисності.
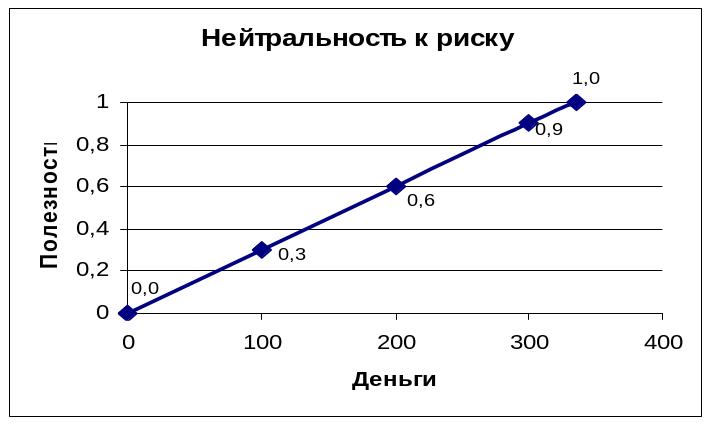
Рис. 8. Функція корисності для ОПР, байдужої до ризику
Ця функція має такі властивості
1. Функція корисності для ОПР, байдужої до ризику не спадна, тому що больша кількість грошей завжди привабливіша їхменшої кількості.
2. ЇЇ графік – лінійна функція. Це означає, что відносна корисність грошей зростає.
Наприклад, якщо при початковій сумі 200 грн. ви отримаєте з певного джерела (виграєте) 100 грн., то корисність зросте на величину
U(300) - U(200) =
Якщо ж при початковій сумі 200 грн. ви втратите (програєте) 100 грн., то корисність зменшиться на величину
U(200) - U(100) =
ОПР байдужа у виборі між отриманням гарантованої суми, що збігається зі сподіваним виграшем, та участю у лотереї.
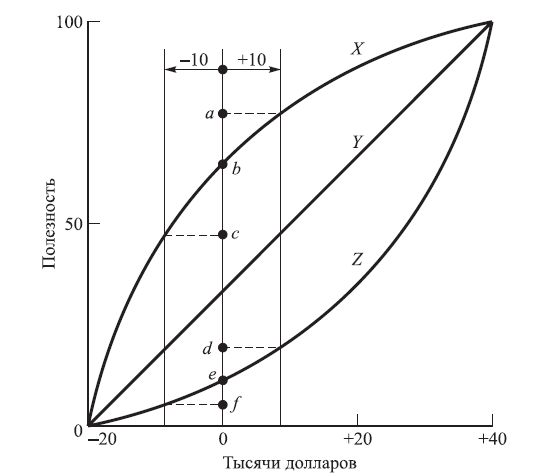
Рис. 9. Функція корисності для осіб, що по різному відносяться до ризику
Можна зробити висновок, що ставлення до ризику —
Аналітично функції корисності такого типу можна задати за допомогою різних функцій розподілу ймовірностей, а саме:
Наприклад, виходячи з нормального закону розподілу, що має параметри m та , отримуємо:
.
НЕЙТРАЛЬНІСТЬ ДО РИЗИКУ
Проміжне значення між схильністю та несхильністю до ризику відіграє нейтральність (байдужість) до ризику. Вона визначається байдужістю особи у виборі між отриманням гарантованої суми, яка збігається з середньоочікуваним виграшем, та участю у лотереї.
Очевидно, що
а) функція корисності для особи, нейтральної до ризику, є лінійною, тобто
U(x) = ax + b;
б) умова байдужості до ризику:
U(M(Х)) = M(U(Х));
в)
величина
сподіваного виграшу збігається з
детермінованим еквівалентом лотереї
(
),
а тому премія
за ризик (Х)
= 0.
Твердження 3. При зростаючій функції корисності для всіх невироджених лотерей особа, яка приймає рішення, тоді і тільки тоді є:
а) несхильною до ризику, коли премія за ризик є додатною ( (Х) > 0);
б) схильною до ризику, коли премія за ризик є від’ємною ( (Х) < 0);
в) нейтральною до ризику, якщо премія (Х) = 0.
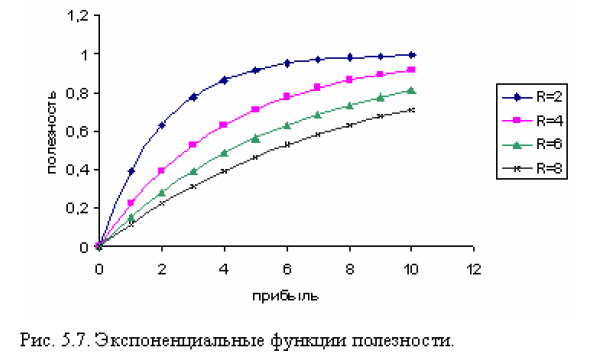
Функція має вид
U(x) = 1 – e-x/r,
де х— грошова сума, якій ми повинні приписати певне значення корисності. Функція залежить від одного невідомого параметра r, який визначає ОПР схильна до ризику. Чим більше значення r, тим менше компанія або ОПР уникає ризику (тобто вони можуть піти на більший ризик). І, навпаки, чим менше значення r, тим більше компанія або індивідум уникає ризику.
Існує багато способів визначення значения параметра r.
Задача 1 Оцінювання корисності доходу. Припустимо, ви заощадили 5000 грн, щоб наступного року придбати меблі. Знайомий бізнесмен пропонує вам укласти гроші в його бізнес. У разі невдачі ви втрачаєте 5000 грн і можливість купити меблі. У разі успіху через рік ви одержуєте 30 000 грн. Фахівець із маркетингу оцінює ймовірність успіху в 0,3. Альтернативний варіант — покласти гроші в банк під 9 % річних без жодного ризику. Яке рішення ви приймете?