Тема: Ризик та елементи теорії корисності

1. Концепція корисності. Пріоритети та їх числове відображення

2. Поняття лотереї. Корисність за Нейманом. Сподівана корисність. Приклади функцій корисності. Аксіоми раціональної поведінки.

3. Детермінований еквівалент лотереї. Страхова сума. Премія за ризик.

4. Різне ставлення до ризику та функція корисності: Умови схильності, несхильності, байдужості до ризику.

1. Концепція корисності. Пріоритети та їх числове відображення

КОРИСНІСТЬ виражає ступінь задоволення, яке одержує суб’єкт від споживання товару чи виконання будь-якої дії.

Співвимірність цінних паперів, які також є товаром, на перший погляд, простіше здійснити, оскільки усі вони мають ціну. Але ризиковані цінні папери — це документи, котрі засвідчують можливість одержання грошей у майбутньому, і тут співвимірність проблематична: не можна сказати, яка з випадкових величин, що відображає ефективність (норму доходу) кожного з цінних паперів, буде більшою чи меншою, а отже, не можна сказати, який з цінних паперів чи який портфель цінних паперів є пріоритетнішим.

Для формального опису співвідношень пріоритету використовують, відповідно, символи, а саме:

«не гірше за» - .

«краще за» - ;

«байдуже» («еквівалентне») - ;

Нестроге співвідношення пріоритетності «не гірше, ніж» є одним із основних найпростіших понять. Запис x  y, де х та у є набором товарів чи послуг (точками простору Х), означає, що певний суб’єкт (споживач) вважає для себе набір х або пріоритетнішим, ніж набір у, або не робить між ними різниці, тобто х не гірше, ніж у. Можна визначити поняття байдужості та строгої пріоритетності: набори товарів х та у байдужі (еквівалентні) для споживача (х  у) тоді і лише тоді , коли

х y та у x .

Коли споживач бажає обрати х, а не у, тобто х пріоритетніше, ніж у (записують х  y), то це відбувається тоді, коли х не гірше за у, а у гірше за х. Тобто, х  y тоді і лише тоді, коли х y і при цьому твердження, що у x, є несправедливим.

Якщо через х позначити набір товарів (послуг тощо), через Х — множину всіх можливих наборів товарів, вважаючи при цьому, що вона є неперервною, то можна побудувати неперервну дійсну функцію U(x), визначену на елементах множини Х, яку називають функцією корисності і для якої U(x) > U(y), якщо х  у.

ГРАНИЧНА КОРИСНІСТЬ вимірює додаткове задоволення, що його одержує особа від споживання додаткової кількості товару.

2.Корисність за Нейманом

Поняття лотереї

Для цього необхідно з множини Х пред’явлених експертам значень певного економічного показника (об’єкта) виділити два значення х_* та х_* таких, що х х_* та х х_* для всіх х  Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне, в певному сенсі, значення показника (разом з «нулем» вони визначають масштаб даної шкали). Власне, так побудована функція корисності Дж. ф. Неймана і О.Моргенштерна. Експерту пропонують порівняти між собою дві альтернативи:

1) значення показника х;

2) лотерею: одержати х_* з імовірністю 1 – р чи х_* з імовірністю р. Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L(х_*, p, x_*) не стануть еквівалентними, тобто x  L(х_*, p, х_*).

Максимальному й мінімальному значенням х_* та х_* приписують довільні числові значення U^*= U(х_*) та U_* = U(x_*), але так, щоб U^* > U_*.

Під лотереєю L(x_*, p(x), x_*) розуміють ситуацію, у якій особа може отримати х_* з імовірністю р(х) або х_* з імовірністю 1 – р(х). (Часто використовують запис: L(x_*, p(x); x_*, q(x)), де q(х) = 1 – р(х)).

За Нейманом корисність варіанта х визначається ймовірністю U(х) = р(х), при якій особі байдуже, що обирати: х — гарантовано, чи лотерею L(х_*, р(х), х_*), де х_*, х_* — вектори, більш та менш пріоритетні порівняно з х, х — варіант економічного ефекту (наприклад, обсяг грошової винагороди).

Наприклад, як функцію корисності можна вибрати функцію

бо для всіх x  [x_*, x_*] значення q(х)  [0; 1]. Оскільки при зростанні х від х_* до х_* значення q(х) будуть збільшуватися, то вибрана таким чином функція корисності буде зростаючою.

Якщо покласти

то в цьому випадку ми отримаємо спадаючу функцію корисності (p(x) = 1 – q(x); p(x)  [0, 1] для x  [x_*, х_*]).

У якості функції корисності (згідно з Нейманом) можна використати функції розподілу ймовірностей:

U(x) = F(x) = P(X < x).

Hаприклад:

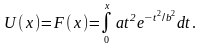
СПОДІВАНА КОРИСНІСТЬ

Нехай L — лотерея, що приводить до виграшів (подій) x₁, х₂, ...., х_n з відповідними ймовірностями p₁, p₂, ..., p_n. Позначимо сподіваний виграш (математичне сподівання виграшу) через :

Справедлива основна формула теорії сподіваної корисності:

тобто корисність ансамблю результатів збігається з математичним сподіванням корисності результатів.