7. Пуассон формуласы
Егер -рет тәжiрибеде оқиғасы өте аз ықтималлдық -мен пайда болса, ал өте үлкен сан болса, онда Пуассон формуласын қолданады.
(7)
Дискреттi кездейсоқ шамалар
Анықтамалар.
1. Кездейсоқ (оқиға емес !) шама дегенiмiз белгiлi комплекс шарттар орындалған тәжiрибеде алдын ала белгiсiз мәндер қабылдайтын шама.
2. Егер шама дискреттi мәндер қабылдаса, кездейсоқ шама дискреттi кездейсоқ шама (Д.К.Ш.)
3. Егер К.Ш. үздiксiз мәндер қыбылдаса, онда кездейсоқ үздiксiз шама (К.Ү.Ш.)
4.
Д.К.Ш. мүмкiн мәндерi өсу
бағытында сол мәндерге
сәйкес К.О. (кездейсоқ оқиға)
ықтималдықтарының
арасындағы
байланыс Д.К.Ш. үлестiрiм
(таралым) заңы
деп аталады.
-
Д.К.Ш. мәндерi.
Дискреттi кездейсоқ шамалардың сандық мiнездемелерi
Кездейсоқ шаманың (К.Ш.) үлестiрiм заңынан басқа оны сипаттайтын сандық мiнездемелер де бар.
Анықтама
1. К.Ш.
математикалық
үмiтi деп, оның мәндерiнiң
олардың сәйкес
ыктималдықтарының
көбейтiндiлерiнiң қосындысын
айтады.
, (
болу мүмкiн) (1)
Анықтама 2. К.Ш. дисперсиясы деп, оның мәндерiнiң математикалық үмiттерiнен ауытқуының квадратының математикалық үмiтi.
(2)
Қасиеттерi.
ж.б. тәуелсiз
К.Ш.
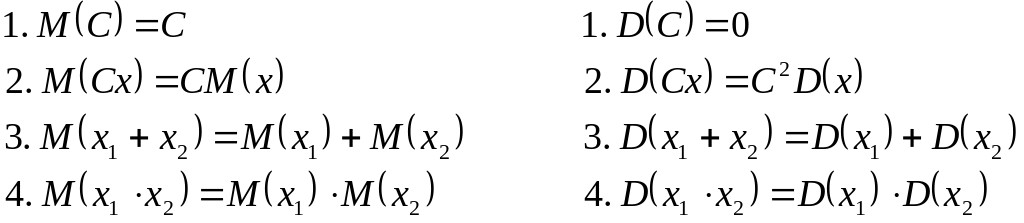
Анықтама 3. К.Ш. орта квадраттық ауытқуы деп
-
айтады (3)
Мысалдар
1. Биномдық (Бернулли) үлестiрiм заңы үшiн
(4)
2.
Пуассон үлестiрiмi
үшiн
(5)
Қорытынды мен ескертулер
Д.К.Ш. үлестiрiм заңының таблицасында I-жолда К.Ш. мәндерi өспелi түрде жазылады. Сәйкес ықтималдықтары II-жолға жазылып,
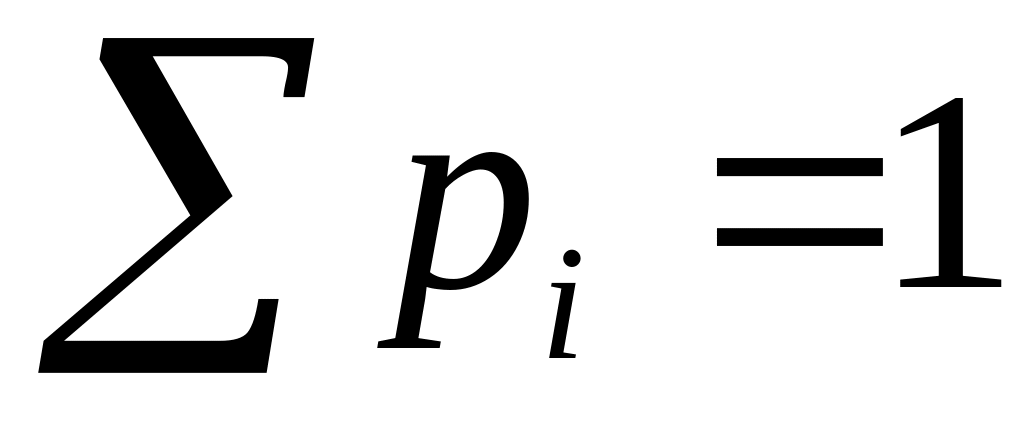тексерiлуi керек.К.Ш. қосындысы, айырымы, көбейтiндiсi тек екi шама емес, кезкелген шамалар үшiн де қолданылады.
Егер К.Ш. қосындысының, айырымының, көбейтiндiсiнiң сәйкес ықтималдықтарын тапқанда а) құраушы шаманың ықтимадығы олардың көбейтiндiсi түрiнде алынады; б) шамалардың мәндерi тең болып кетсе, онда ол ортақ (бiр) шама үшiн ықтималдықтарының қосындысы алынады.
-
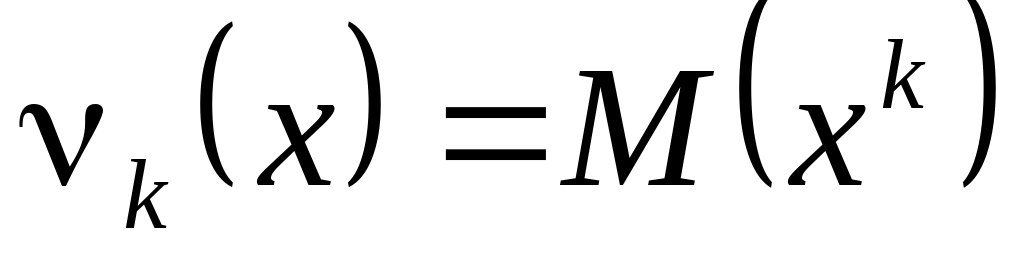бастапқы момент, (6)
-
орталық момент деп,
(7)
ал
- ретi деп аталады.
Мысалы,
- математикалық үмiт -
бiрiншi реттi бастапқы
момент;
екiншi реттi орталық момент.
Ал
-
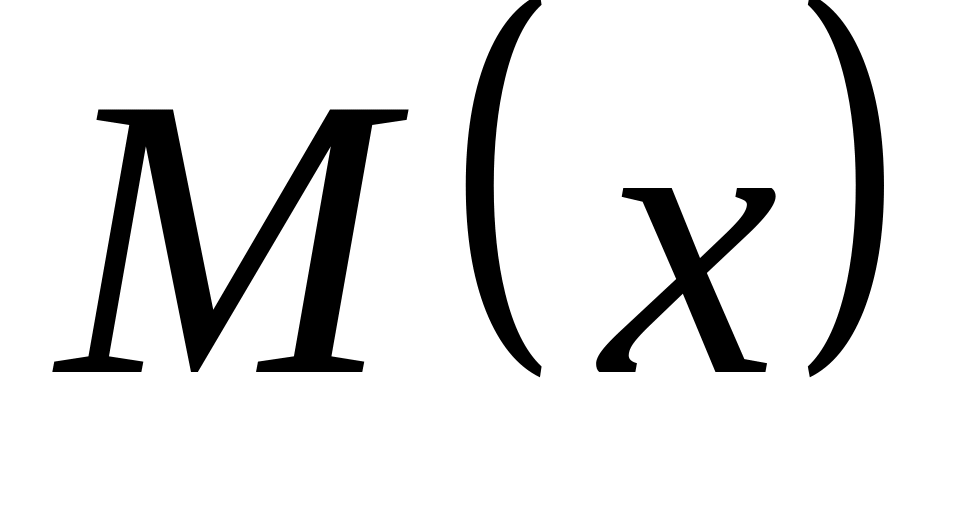К.Ш. мәндерiнiң шоғырланатын
орнын (ауырлық центрi немесе орта мән
тәрiздi) анықтайды ал
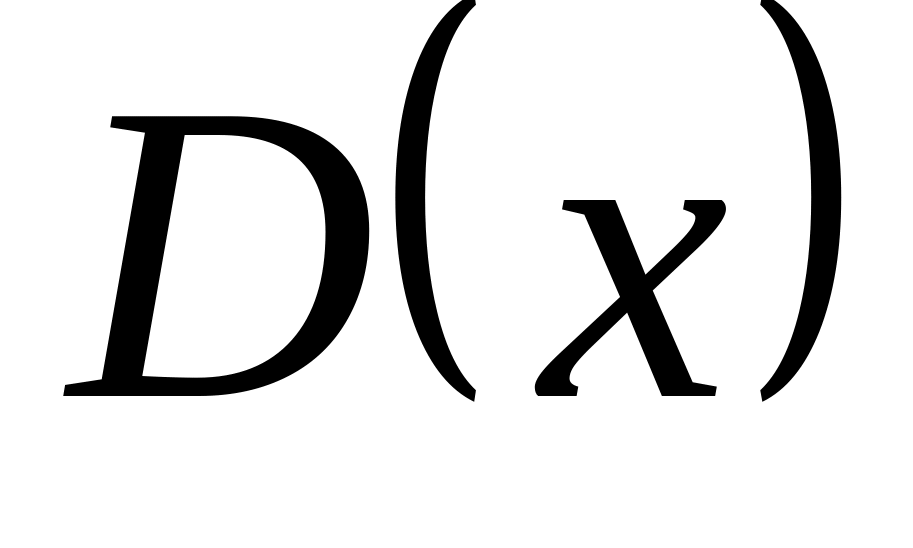және
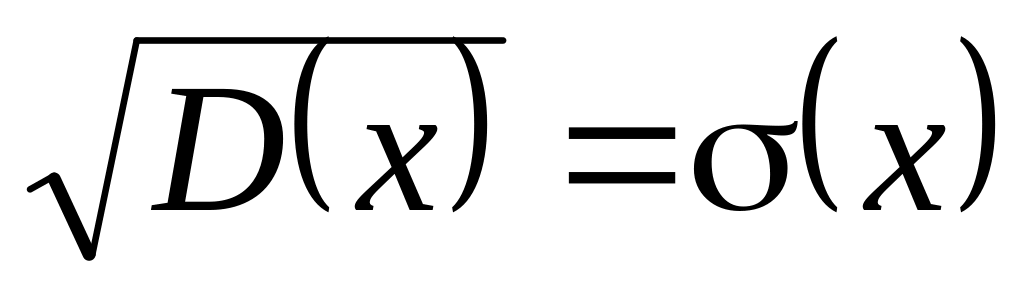- К.Ш. математикалық
үмiттен (
-туралы
болжам) қаншалықты ауытқуын
(сан арқылы) айқындайды. Сондықтан да
олар сандық мiнездемелер (К.Ш.
мiнездеме)
деп аталады.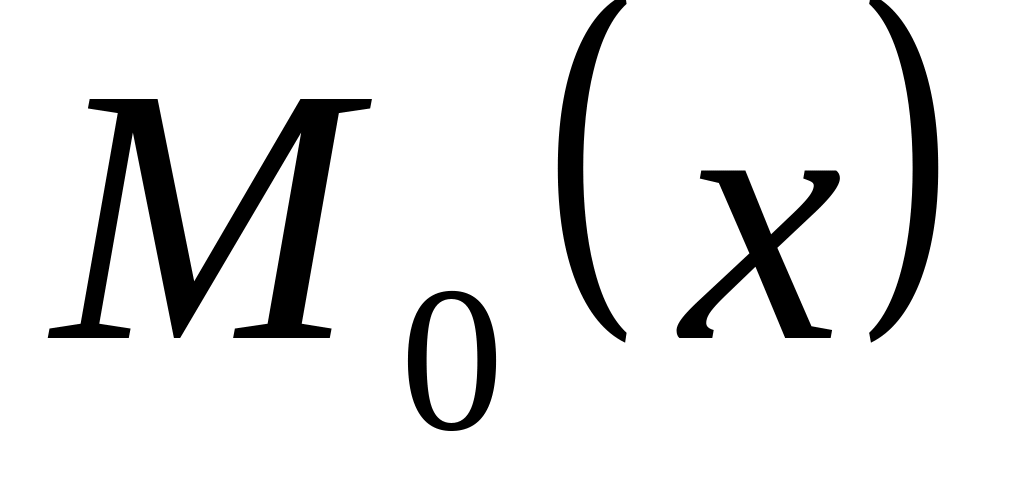
-
мода
дегiнiмiз -
ықтималдықтарының ең
үлкенiне сәйкес келетiн К.Ш. мәнi
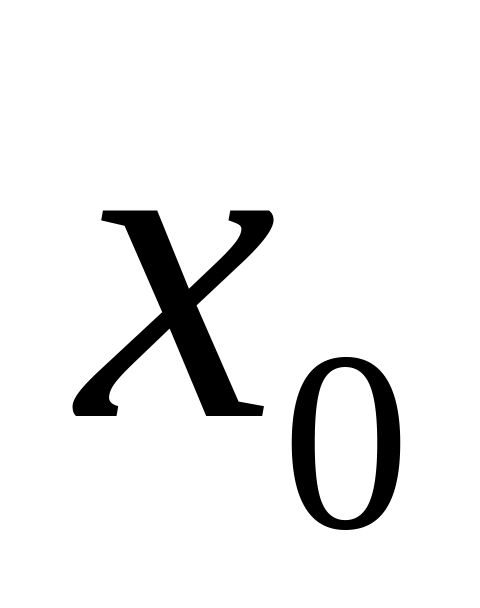(8)
-
медиана -
үлестiрiмдегi ықтималдықтардың екi
жағынан қосынды мәндерi тең болуына
сәйкес келетiн К.Ш. мәнi
(9)
К.Ш. үлестiрiмiнiң асимметриясы -
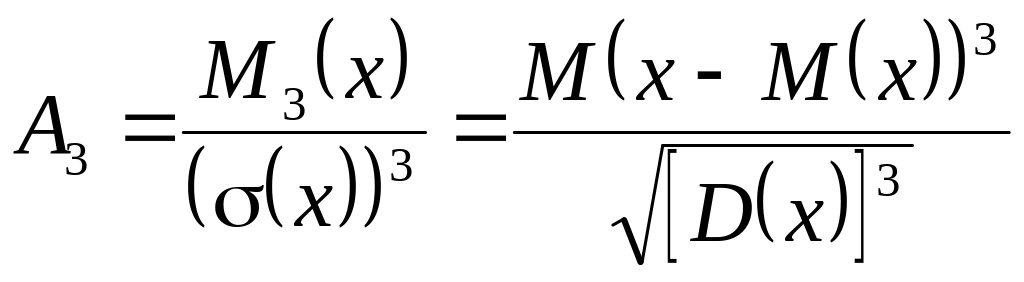- саны (10)К.Ш. үлестiрiмiнiң эксцессi -
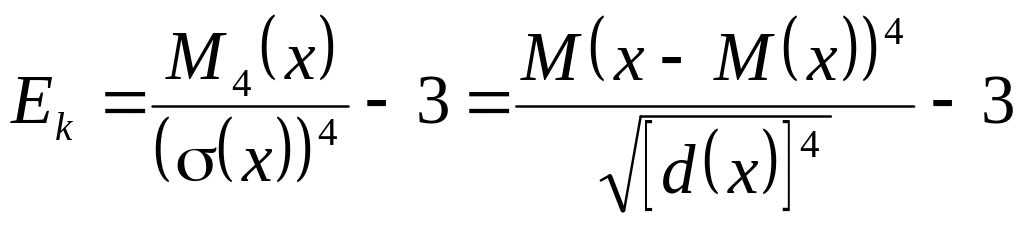- саны (11)
Келтiрiлген жаңа ұғымдар К.Ш. ықтималықтары мен олардың үлестiрiмiнiң қалай екенiн айқындайтын мiнездеме түсiнiктер.