2.1. Коллинеарность векторов
Проверить
коллинеарность векторов
=
2
+4
и
=
–
–2
,
построенных по векторам
=(-1;
5; 2) и
=(3;
2; -2).
Решение.
= (-2+12; 10+8; 4–8) = (10; 18; -4);
= (1–6; -5–4; -2+4) = (-5; -9; 2);
=
=
=> –2 = –2 = –2 => векторы
и
коллинеарны.
2.2. Скалярное произведение векторов
Даны
точки А(2; -1; 5), B(5; 3; 10), C(6; 4; 2). Найти длины
векторов
и
;
скалярное произведение
·
,
а также угол между ними. Вычислить
.
Решение.
=(5-2; 3-(-1); 10-5) = (3; 4; 5);
=(6-2; 4-(-1); 2-5) = (4; 5; -3);
;
;
∙ = 12 + 20 – 15 = 17;
cos
φ =
;
φ = arccos
.
.
2.3. Действия над векторами
Даны точки А(2; 1; 3), B(-1; 3; 5), C(4; -4; 6).
Вычислить: · ; ( + )2; (3 -2 )·( +3 ).
Решение.
1 Способ.
=(-1-2; 3-1; 5-3) = (-3; 2; 2); =(4-2; -4-1; 6-3) = (2; -5; 3);
;
;
· = –6 – 10 + 6 = -10;
( + )2 = (-3+2; 2+(-5); 2+3) 2 = (-1; -3; 5) 2 = 1 + 9 + 25 = 35;
2-й способ.
По свойствам скалярного произведения
(
+
)2
=
+2
·
+
=
+2
·
+
=
+2(-10)
+
=
35.
(3 -2 )·( +3 ) = 3 +7 · –6 = =3 +7(-10) –6 = 51 – 70 – 228 = –247.
2.4. Разложение вектора по базису
2.4.1. На плоскости
Разложить вектор (7; 4) по базису (1; 2), (2; -1).
Решение.
α∙ + β∙ = ,
α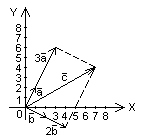
(
)+
β(
)
= (
),
=>
=
,
=>
,
=>
.
Ответ: = 3 + 2 .
Рисунок 2 –Разложение вектора
2.4.2. В пространстве
Даны
векторы
(1;
0; 1),
(0;
2; -1),
(3;
1; 0) и
(-1;
0; 4). Найти разложение вектора
(
)
по базису
,
,
.
Решение. α∙ + β∙ + γ∙ = ,
=> (α; 0; α) + (0; 2β; -β) + (3γ; γ; 0) = (-1; 0; 4),
=> (α + 3γ; 2β + γ; α – β) = (-1; 0; 4).
Записываем равенство соответствующих координат в виде системы уравнений, которую можно решить по формулам Крамера или методом Гаусса, или методом обратной матрицы.
.
Решая систему по формулам Крамера, получаем
,
,
,
;
,
,
;
=> (5; 1; -2).
2.5. Векторное произведение
Даны
векторы
=(-1;
5; 2) и
=(3;
2; -2). Вычислить 1)
;
2)
;
3)
.
Решение.
2)
3)
2.6. Площадь параллелограмма
Даны точки А(1; 0; 0), В(0; 5; -1), C(-2; 1; 2). Вычислить площадь параллелограмма, построенного на векторах и .
Решение.
=(0-1; 5-0; -1-0) = (-1; 5; -1),
=(-2-1; 1-0; 2-0) = (-3; 1; 2),
S
=
(кв.ед.).
2.7. Компланарность векторов
Даны
точки А(1; 2; -5 ), В(2; -1; -10), C(-1; 3; 0) и D(-4; -2;
1). Являются ли векторы
,
,
компланарными? Выяснить, является ли
тройка векторов
,
,
правой, если векторы некомпланарны?
Вычислить направляющие косинусы вектора
.
Решение.
=(2-1; -1-2; -10-(-5)) = (1; -3; -5),
=(-1-1; 3-2; 0-(-5)) = (-2; 1; 5),
=(-4-1;
-2-2; 1-(-5)) = (-5; -4; 6);
=>
векторы
,
,
компланарны.
;
;
.
2.8. Смешанное произведение
Даны четыре точки А(1; 2; 0), В(-1; 2; 1), C(-1; -1; -1) и D(0; 1; 3). Вычислить объем треугольной пирамиды, построенной на векторах , , и длину высоты, опущенную из точки D, на плоскость основания. Является ли тройка векторов , , правой?
Решение.
=(-1-1; 2-2; 1-0) = (-2; 0; 1),
=(-1-1; -1-2; -1-0) = (-2; -3; -1),
=(0-1; 1-2; 3-0) = (-1; -1; 3);
;
Так
как
> 0, то тройка векторов – правая.
(куб.ед.);
;
SАВС
=
(кв.ед.).
H
=
(ед.).