1 Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 17.1.1. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рис. 17.1.1. Выборочные функции случайного процесса.

С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n;t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

1. Стационарные случайные процессы.

Случайный процесс называется стационарным в строгом (узком) смысле, если его функция распределения любого порядка не изменяется при сдвиге совокупности точек на величину , т.е. Другими словами, для стационарного процесса функция распределения любого порядка и, следовательно, его характеристики не зависят от положения начала отсчета времени. Стационарность означает статистическую однородность процесса во времени. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме, каковым является, например, шум на выходе усилителя через достаточно большой промежуток времени после его включения.

Если приведенное выше условие не выполняется, то процесс называется нестационарным. Нестационарный процесс будет наблюдаться, например, на выходе какого-либо генератора шумов непосредственно после его включения.

Из определения стационарного процесса следует, что

т.е. одномерная функция распределения вообще не зависит от времени, а двумерная функция распределения зависят только от разностей времен . Отсюда следует, что для стационарного случайного процесса среднее значение и дисперсия являются постоянными величинами, т.е. не зависит от времени

а корреляционная функция такого процесса зависит только от одной переменной :

случайный процесс называют стационарным в широком смысле, если его среднее значение и дисперсия не зависят от времени, а корреляционная функция зависит только от разности времен . Стационарность в широком смысле не тождественна строгому определению стационарности. Случайные процессы, стационарные в строгом смысле, всегда стационарны в широком смысле, но не наоборот.

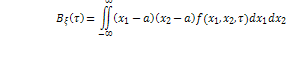
Глава 17 стационарные случайные функции

17.1. Понятие о стационарном случайном процессе

На практике очень часто встречаются случайные процессы, протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени. Такие случайные процессы называются стационарными.

В качестве примеров стационарных случайных процессов можно привести: 1) колебания самолета на установившемся режиме горизонтального полета; 2) колебания напряжения в электрической осветительной сети; 3) случайные шумы в радиоприемнике; 4) процесс качки корабля и т. п.

Каждый стационарный процесс можно рассматривать как продолжающийся во времени неопределенно долго; при исследовании стационарного процесса в качестве начала отсчета можно выбрать любой момент времени. Исследуя стационарный процесс на любом участке времени, мы должны получить одни и те же его характеристики. Образно выражаясь, стационарный процесс «не имеет ни начала, ни конца».

Примером стационарного случайного процесса может служить изменение высоты центра тяжести самолета на установившемся режиме горизонтального полета (рис. 17.1.1).