Сложность арифметических операций.

Алгоритм решения вычислительной задачи представляет собой некоторую процедуру, выполняемую над набором данных, т.е. с некоторой информацией, записанной в цифровом виде в виде знаков некоторой системы счисления.

В процессе переработки информации приходится выполнять арифметические действия.

В связи с этим возникает задача выбора наиболее эффективных способов решения, выбора эффективных алгоритмов.

Для изучения алгоритма прибегают к оценке его сложности. Оценить сложность - значит сосчитать с достаточной точностью число элементарных операций, необходимых для его выполнения при фиксированных данных.

Для простоты будем считать, что числа заданы в двоичной системе счисления.

Пусть число n є N в двоичной записи имеет число цифр S+1, т.е.

n = n₀+ n₁*2+ n₂*2² + …+ n_s*2^s ; , где n_s = 1

Значит 2^s ≤ n < 2^s+1 ⇒ S ≤ log₂ n < S+1

Иногда вводят как обозначение log N – длина записи числа N.

В качестве оценки сложности алгоритма обычно выбирается время его работы. (max время для всех наборов данных).

Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное её значение бессмысленно. Дело в том, что во-первых, точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций, битовых операций или операций на машине Тьюринга), а во-вторых, при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, фигурирующих в выражении для точного времени работы, становится крайне незначительным.

Опр. Порядком роста функции f в точке z₀ называется некоторое число α ≥ 0 такое, что для некоторой окрестности U₀ существует такое число M > 0, что для произвольной точки z ϵ U₀ выполняется неравенство

Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма. При этом алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных, за исключением лишь, возможно, данных малого размера. Для записи асимптотической сложности алгоритмов используются асимптотические обозначения:

Обозначение	Интуитивное объяснение	Определение
	f ограничена сверху функцией g (с точностью до постоянного множителя) асимптотически	Или
	f ограничена снизу функцией g асимптотически
	f ограничена снизу и сверху функцией g асимптотически	<
	g доминирует над f асимптотически
	f доминирует над g асимптотически
	f эквивалентна п асимптотически

Примеры

1.«Пропылесосить ковер» требует время, линейно зависящее от его площади , то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз, и т. п.

2.«Найти имя в телефонной книге» требует всего лишь время, логарифмически зависящее от количества записей , так как открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге, толщиной в 1000 страниц, любое имя находится не больше чем за   раз (открываний книги). При увеличении объема страниц до ста тысяч, проблема все еще решается за   заходов.

 данные – множество чисел, которые в некоторых системах счисления имеют длину ≤ n

Тогда сложность алгоритма оценивается некоторой функцией , т.е. зависящей от n.

 даны два алгоритма с и – функции сложности

, т.е.

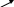
в таком виде обычно получают оценки сложности алгоритмов.