1.8 Построение кривой свободной поверхности потока по способу Бахметева

Кривые свободной поверхности для нижнего и верхнего участ­ков строят на двух листах миллиметровой бумаги формата A3. Построения выполняют в искаженном масштабе (вертикальный масштаб крупнее горизонтального). Рекомендуемые масштабы:

-горизонтальный 1:5000, 1:10000, 1:20000, 1:25000;

-вертикальный 1:10, 1:20, 1:25, 1:50.

Построения выполняют во втором квадранте: ось абсцисс начинается в правом нижнем углу и направлена справа налево; ось ординат направлена снизу вверх.

Чертеж начинают с нанесения линии дна, которую из-за искажения масштабов намечают не по заданному углу наклона к горизонту, а по катетам, откладываемым в горизонтальном и вертикальном масштабах, ватем, отметив на вертикальной шкале значения нормальной и критической глубин, параллельно дну прово­дят линии нормальных (N-N) и критических (К-К) глубин.

Далее по оси абсцисс откладывают найденные длины l, а по вертикали от линии дна - соответствующие глубины. Полученные точки соединяют плавной кривой. Для каждой расчетной точки кривой свободной поверхности обязательно с помощью размерных линий указывают глубины и на оси абсцисс отмечают длины (рисунок 1.8.1, рисунок 1.8.2).

2 Гидравлический расчет дюкера

2.1 Расчет одной нитки трубопровода

Дюкер (гидротехнический) - это заглубленная труба под рекой, каналом, другими сооружениями для пропуска заданного расхода воды (рисунок 2.1.1). В курсовой работе с помощь дюкера соединя­ются два цилиндрических канала.

Рисунок 2.1.1 – Схема соединения цилиндрических каналов (I и III) различных поперечных сечений и дюкера (II) – плоскость сравнения; 1-1 и 3-3 – поперечные сечения на входе и выходе из дюкера.

Гидравлический расчет дюкера состоит в подборе необходимо­го диаметра трубопровода для пропуска заданного расхода при известных характеристиках русла, дюкера, расхода и разности го­ризонтов воды в сечениях 1-1 и 3-3.

Для этого составим уравнение Бернулли для сечений 1-1 и 3-3 относительно плоскости сравнения 0-0.

где z₁ и z₃ превышение над плоскостью сравнения 0-0 свободной поверхности в сечениях 1-1 и 3-3, тогда z₁-z₃ = Δh; р₁ и p₃- гидродинамические давления в сечениях 1-1 и 3-3, Па;

P₁ = Р_з =P_атм

ρ – плотность жидкости; g – ускорение свободного падения;

, - средние скорости в сечениях 1-1 и 3-3, м/с;

Q – расход воды в системе, м³/с;

ω₁, ω₃ – площадь живого сечения первого и второго каналов;

α – коэффициент кинетической энергии, характеризующий не­равномерность распределения местных скоростей по живому сечению потока, для развитого турбулентного движения α ≈ 1;

- величина потерь напора между сечениями 1-1 и 3-3, м.

С учетом вышесказанного уравнение (2.1.1) можно записать в виде

(2.1.1)

1.Дюкер является коротким трубопроводом, в котором потери напора в местных сопротивлениях соизмеримы с потерями по длине трубопровода; при определении потерь напора учитывают шероховатость труб и местные сопротивления, поэтому

(2.1.2)

Потери напора по длине определяются по формуле Дарси – Вейсбаха

(2.1.3)

где L₂ - длина трубопровода, м;

d- диаметр трубопровода, м;

- скорость воды в дюкере, м/с;

- площадь живого сечения трубопровода, м².

λ - коэффициент гидравлического трения, зависящий от режима движения жидкости.

Согласно исследованиям И. Никурадзе, выделено три зоны: первая - ламинарного режима, вторая - неустойчивого или переходного режима и третья - турбулентного режима, которая в свою очередь разбивается на три области. Первая - «область гидравлически гладких русел», вторая - «область доквадратичного сопротивления гидравлически шероховатых русел», третья - «область квадратичного сопротивления гидравлически шероховатых русел». Движение воды в дюкере происходит при скоростях, соответ­ствующих турбулентному режиму. Области сопротивления определяют по первому (Re_пр1,) и второму ( Re_пp2) предельным числам Рейнольдса

	(2.1.4)
	(2.1.5)

- эквивалентная высота выступов шероховатости, м.

Для чисел Рейнольдса 4000 < Re < Re_пpl получаем область гид­равлически гладких русел. Здесь коэффициент гидравлического трения λ =f (Re) определяется по формуле Блазиусf

(2.1.6)

где ;

ν = 0,01 Ст - кинематический коэффициент вязкости воды для t = 20°С.

В случае Re_пр1, < Re < Re_np2 коэффициент λ =f (Re, Δ) соответствует области доквадратичного сопротивления гидравлически шероховатых русел, для которой справедлива формула Альтшуля

(2.1.7)

Для области квадратичного сопротивления гидравлически ше­роховатых русел Re > Re_пр2, коэффициент гидравлического трения = f(Δ) определяется по формуле Шифринсона

(2.1.8)

В заданном дюкере учитываются местные потери при входе через решетку, два поворота на α градусов и потери на выход.

Потери напора на преодоление местных сопротивлений определяют по формуле

(2.1.9)

где =0,5 - коэффициент местного сопротивления на входе в

трубопровод;

- коэффициент местного сопротивления при прохождении потока через решетку;

- коэффициент местного сопротивления при повороте тру­бопровода;

- потери напора на выходе из трубопровода, м.

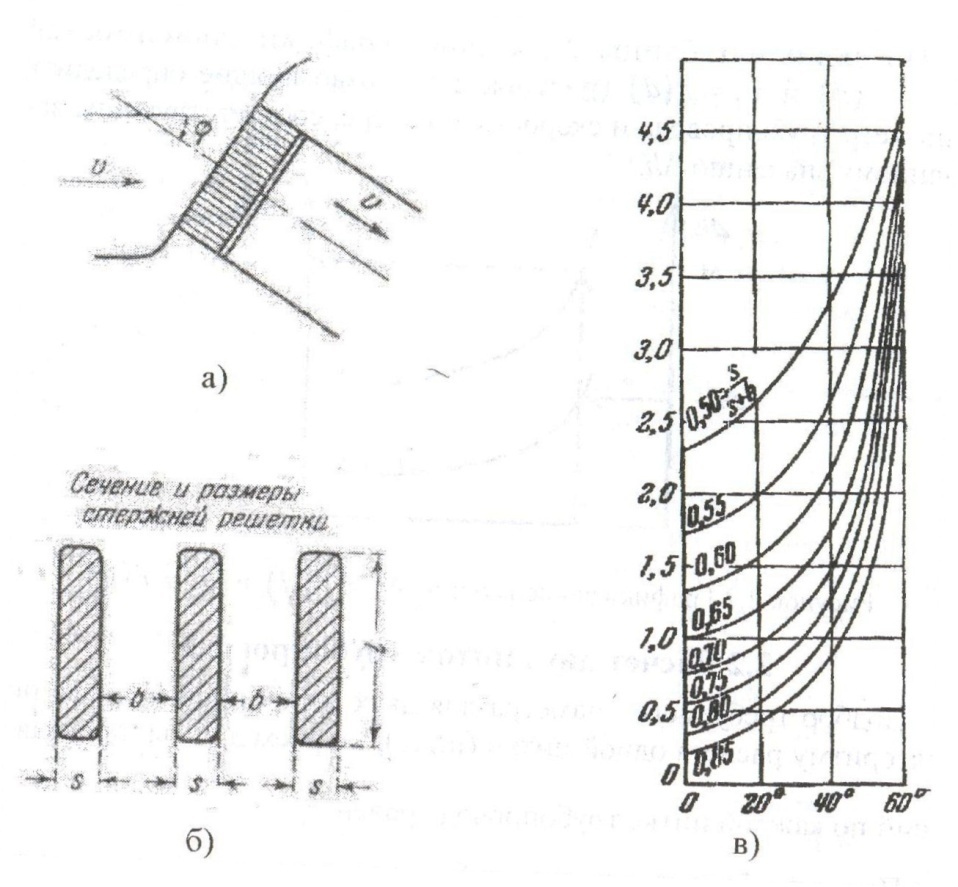
Решетка устанавливается перед входом в дюкер для предотвращения попадания в него различного рода загрязнений (рисунок 2.1.2, а).

При косом расположении решетки (рисунок 2.1.2, а, б) коэффициент ζ_реш для прямоугольных стержней сечением 10x70 мм в зависимости от величины угла φ набегания потока на решетку определяют по графику (рисунок 2.1.2, в).

Для определения ζ_пов используют зависимость

ζпов = A∙B

(2.1.10)

де А и В- параметры, зависящие от величины утла поворота, пред­ставлены в таблице 2.1.1;

Таблица 2.1.1 - Определение параметров коэффициента местного сопротивления при повороте трубопровода

Угол поворота, град.	0	20	30	45	60	75	90	110	130	150		180
А	0	2,50	2,22	1,87	1,50	1,28	1,20	1,20	1,20	1,20		1,20
В	0	0,05	0,07	0,17	0.37	0,63	0,99	1,56	2,16	2,67		3
											(2.1.11)

Рисунок 2.1.2– Решетка стержневая

Изменение диаметра трубопровода (d) влияет на скорость воды в дюкере (v₂), коэффициент гидравлического трения (λ), и на перепад уровней воды в каналах ( ). Расчет диаметра дюкера производится по зависимости (2.1.11). Задаем ряд значений диаметра и определяем Δh. Все расчеты сводим в таблицу 2.1.2

Таблица 2.1.2 - К определению диаметра трубопровода

d, м	ω2, м2	v2, м/с	Re	Reпр2	Область сопротивления	λ	hl	hM	Δh
1	0,785	3,18	3180000	466666,7	Квадр.	0,02	0,19000	2,350	2,54
5	19,630	0,13	650000	2333333	Доквадр.	0,02	0,00006	0,009	0,02
3	7,070	0,35	1050000	1400000	Доквадр.	0,03	0,00100	0,020	0,03
2	3,140	0,70	1580000	933333	Квадр.	0,01	0,00300	0,130	0,14
1,8	2,540	0,98	1764000	840000	Квадр.	0,01	0,00900	0,200	0,21

По данным таблицы 2.1.2 строим графики зависимостей Δh=f(d) и v₂ = f(d) (рисунок 2.1.3), позволяющие определить диаметр трубопровода и скорость в дюкере, соответствующие за­данному значению Δh.