1.4 Определение формы кривой свободной поверхности потока

В зависимости от гидравлических условий, создающихся при возведении сооружений, и состояния потока, глубины по его длине могут увеличиваться (кривая подпора) или уменьшаться (кривая спада).

Форма кривой свободной поверхности устанавливается на основе анализа дифференциального уравнения неравномерного движения третьего вида

(1.4.1)

где .

При этом тип кривой свободной поверхности зависит от зоны, в которой находится заданная глубина.

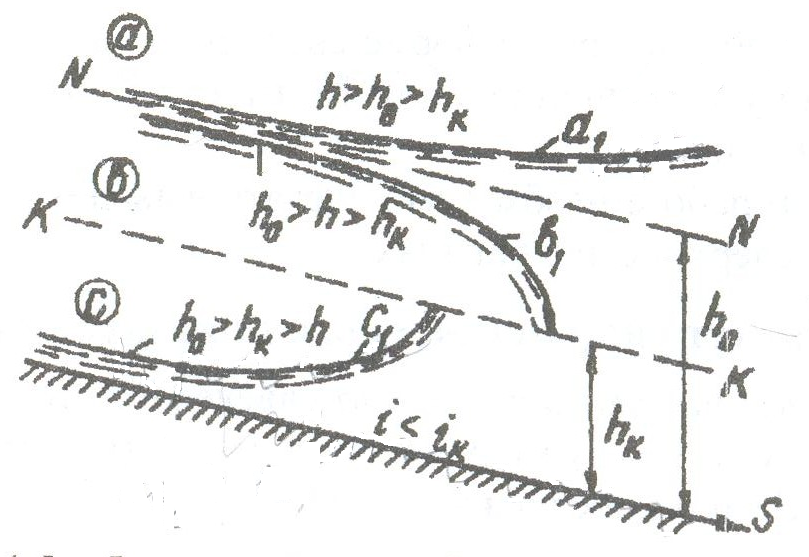
При не равномерном движении в русле с прямым уклоном (i>0) различают три случая, характеризуемые условиями:

h₀ > h_k и i < i_k (рисунок 1.4).1. При этом получаем три возможные формы свободной поверхности: кривые подпора а₁, с₁, и кривую спада b₁.

Рисунок 1.4.1 – Форма кривых свободной поверхности при i < iк

1.5 Расчет гидравлического показателя русла

Гидравлический показатель русла x введен Б. А. Бахметевым для упрощения связи между модулем расхода К и глубиной h. Вместо уравнения Шези он предложил зависимость

(1.5.1)

где h' и h" - произвольные глубины для заданного поперечного сечения, м;

К' и К " - соответствующие им модули расхода, м³/с.

Из зависимости (1.5.1) логарифмированием получена формула для вычисления х:

(1.5.1)

Гидравлический показатель х для некоторых русел считается постоянным и не зависящим от глубины. Это справедливо, например, для узких и широких прямоугольных, узких и широких параболических и треугольных сечений. Для других (прямоугольных, параболических, исключая широкие и узкие, и трапецеидальных) можно приближенно принять х ≈ const. Для более сложных (замкнутого профиля, составных) – х ≠ const, и следовательно, метод Бахметева не может применяться для таких русел.

При вычислении х по формуле (1.5.1) важно правильно выбрать значения глубин. Предлагается в качестве h" принять среднюю глубину на данном участке потока h_ср, и К" = К_ср , а в качестве h' -нормальную глубину h₀ и К' = К₀. Тогда формула (1.5.1) примет вид

(1.5.2)

Для трапецеидального сечения

1,02	3,39	5,48	0,62	46,17	123,24
2,02	9,76	9,08	1,07	50,57	510,55

Для параболического сечения

	, м
1,78	4,77	5,66	6,08	0,93	35,28	192,57
	, м
0,58	2,72	1,05	3,05	0,34	29,84	18,27

1.6 Построение логарифмической анаморфозы

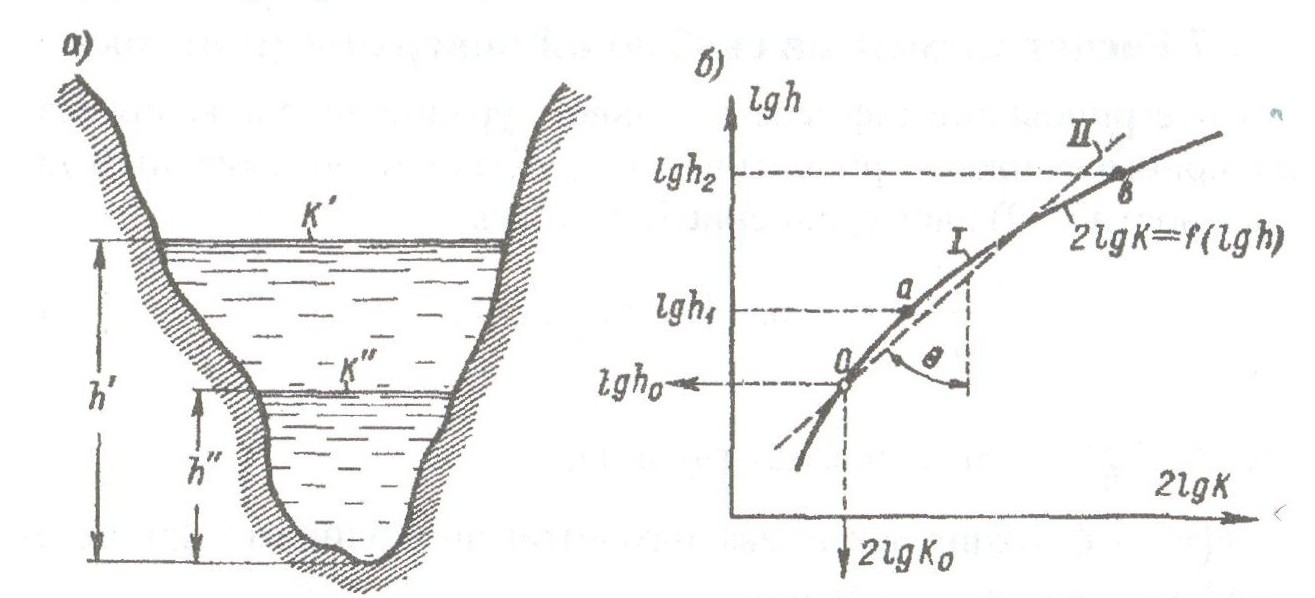
От постоянства гидравлического показателя зависит в принципе применимость выражения (1.5.1) и выведенного с его помощью уравнения Бахметева к расчету и построению кривой свободной поверхности заданного канала. Для окончательного решения вопроса о применимости метода Бахметева необходимо построить график 2lg К = f(lg h), называемый логарифмической анаморфозой (рисунок 1.6.1).

Рисунок 1.6.1 – Логарифмическая анаморфоза

На графике нанесены две линии: I - линия Шези, которая строится по уравнению

(1.6.1)

Для этого задаем ряд значений глубины (не менее 4). Рекомендуемый диапазон принятых значений h: от 0 до 3 м. Расчеты проводим в табличной форме (таблица 1.6.1).

Таблица 1.6.1 – К построению линии Шези

а) трапецеидальное сечение

h, м	lg h	ω, м2	χ, м	R, м	С, м0,5/с	K, м3/с	2lg K
0,50	-0,30	1,28	3,60	0,36	42,17	32,39	3,02
1,00	0,00	3,30	5,41	0,61	46,05	118,69	4,15
1,50	0,18	6,08	7,21	0,84	48,57	270,65	4,86
2,00	0,30	9,60	9,01	1,07	50,57	502,18	5,40

б) параболическое сечение

h, м	lg h	ω, м2	χ, м	R, м	С, м0,5/с	K, м3/с	2lg K
1,30	0,11	3,54	5,18	0,68	33,49	97,76	3,98
1,80	0,26	5,76	6,13	0,94	35,35	197,41	4,59
2,30	0,36	8,33	7,41	1,12	36,39	320,80	5,01
2,80	0,45	11,18	8,64	1,29	37,26	473,13	5,35

II - линия Бахметева - это прямая, построенная по зависимости (1.7), где h" - любая действительная глубина из принятого диапазона глубин, h' = h₀ и К’ = K₀.

Согласно уравнению (1.6.1) линия Бахметева обязательно проходит через точку с координатами lg h₀ и 2lg K₀. Эта точка является общей для обеих линий.

Таблица 1.6.2 – К построению кривой свободной поверхности по способу Бахметева.

а) трапецеидальное сечение

h″	lg h″	x∙lg h″	2lg K′ - x∙lg h′	2lg K″
1,00	0,00	0,00	4,15	4,15
2,00	0,30	1,27	4,15	5,40

б) параболическое сечение

h″	lg h″	x∙lg h″	2lg K′ - x∙lg h′	2lg K″
1,80	0,26	1,08	4,59	4,59
2,80	0,45	1,87	4,59	5,35

И при трапецеидальном сечении, и при параболическом линии I и II располагаются рядом (рисунок 1.6.2, рисунок 1.6.3), т. е. линия I близка к прямой, следовательно, для дальнейших расчетов можем использовать выражение 1.5.1.