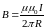Правила Кирхгофа

Д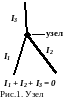 ля разветвленных цепей сформулированы два правила, которые позволяют рассчитать ток и напряжение на любых участках.

Назовем узлом точку, в которой сходится не менее трех токов (рис.1).

Если в цепь не включен конденсатор, то заряд в узле не теряется, поэтому сумма токов, входящих в узел и токов, выходящих из узла, должна быть одинакова. Токи, входящие в узел возьмем со знаком «+», а выходящие из узла со знаком «-», тогда первое правило Кирхгофа имеет вид:

Сумма токов, сходящихся в узле, равна нулю.

Н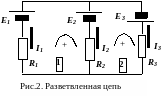 а рисунке 2 показана разветвленная цепь, которую удобно разбить на три контура:

Контур 1, содержащий источники тока Е₁ и Е₂ и сопротивления R₁ и R₂, контур 2, содержащий источники Е₂ и Е₃ и сопротивления R₂ и R₃, контур 3, содержащий источники Е₁ и Е₃ и сопротивления R₁ и R₃. Для любого из этих контуров сумма падений напряжений на участках контура равна сумме ЭДС, работающих в контуре. Выбрав положительное направление обхода токов как показано на рисунке, для каждого из контуров получим:

1: I₁R₁ – I₂R₂ = E₁ – E₂

2: I₂R₂ + I₃R₃ = E₂ + E₃

3: I₁R₁ + I₃R₃ = E₁ + E₃

Применение закона Ампера

1. Рамка с током во внешнем магнитном поле.

Р ассмотрим рамку с закрепленной осью со сторонами l и 2r, по которой течет ток I, находящуюся во внешнем магнитном поле с индукцией B. На каждую сторону l действует сила Ампера , создающая вращающий момент. Суммарный момент, действующий на рамку равен . Вводя понятие магнитного момента рамки с током , получим связь магнитного и механического моментов: .

2. Взаимодействие проводников с током.

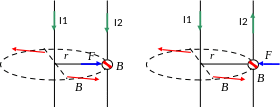
Рассмотрим два параллельных бесконечных проводника с токами I₁ и I₂, находящиеся на расстоянии r друг от друга. Пусть проводник с током I₁ создает поле, а проводник с током I₂ в него попадает. Индукция магнитного поля первого проводника 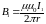. По закону Ампера сила, действующая на единицу длины второго проводника равна , по третьему закону Ньютона она равна силе, действующей со стороны второго проводника на первый. Направление индукции магнитного поля и силы Ампера определяется правилом буравчика.

Расчет магнитных полей различных проводников с током

1. Виток с током.

Р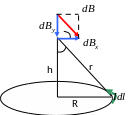 ассмотрим круговой виток с током, каждый элемент которого Idl создает на расстоянии h от центра витка поле с индукцией dB. По закону Био-Саварра-Лапласа индукция равна 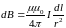, так как элемент контура dl и радиус-вектор r лежат во взаимно перпендикулярных плоскостях. Тогда 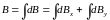. В силу осевой симметрии кольца , значит, . Из рисунка видно, что , тогда вынося за знак интеграла константы и интегрируя, получим 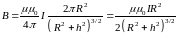. Чтобы найти индукцию магнитного поля в центре витка, положим h = 0 и тогда

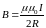
2. Прямой провод.

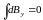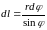Р ассмотрим прямой проводник, каждый элемент тока которого создает поле с индукцией dB. По закону Био-Саварра-Лапласа индукция равна , тогда . В силу осевой симметрии , значит, . Из рисунка видно, что , а элемент контура , тогда 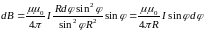. Интегрируя получим . Если провод бесконечный, интегрирование проводится от ₁ = 0 до ₂ = , тогда