
- •Электрическое поле
- •Электрическое поле Электрический заряд. Закон Кулона
- •Электроскоп. Проводники и непроводники электричества
- •Закон Кулона
- •Теорема Гаусса.
- •Диэлектрики во внешнем электрическом поле.
- •Проводники в электрическом поле. Электроемкость. Конденсаторы.
- •Энергия конденсатора.
- •Постоянный электрический ток.
- •Уравнение непрерывности.
- •Закон Ома для замкнутой цепи.
- •Магнитостатика.
- •Работа по перемещению проводника в магнитном поле
- •Токи смещения и уравнения Максвелла
- •Правила Кирхгофа
- •Применение закона Ампера
- •Расчет магнитных полей различных проводников с током
- •Виток с током.
- •Прямой провод.
- •Применение теоремы о циркуляции
- •Расчет напряженностей и потенциалов электрических полей
- •Р асчет полей с помощью закона Кулона
- •Поле заряженной нити
- •Напряженность на оси кольца
- •Бесконечная заряженная плоскость
- •Расчет электроемкостей уединенных проводников и конденсаторов
- •Соединение конденсаторов.
- •Соединение проводников.
Закон Кулона
С ила
взаимодействия точечных зарядов прямо
пропорциональна произведению их модулей,
обратно пропорциональна расстоянию
между ними и направлена вдоль линии,
соединяющей центры зарядов
ила
взаимодействия точечных зарядов прямо
пропорциональна произведению их модулей,
обратно пропорциональна расстоянию
между ними и направлена вдоль линии,
соединяющей центры зарядов 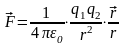 (1), где ε0 = 8,85∙10-12 Ф/м, q1
и q2 – величины
взаимодействующих зарядов, r
– расстояние между зарядами. Для удобства
описания взаимодействия введем понятие
электрическое поле – это особый
вид материи посредствам которого
взаимодействуют заряды.
(1), где ε0 = 8,85∙10-12 Ф/м, q1
и q2 – величины
взаимодействующих зарядов, r
– расстояние между зарядами. Для удобства
описания взаимодействия введем понятие
электрическое поле – это особый
вид материи посредствам которого
взаимодействуют заряды.
Напряженность электрического поля
– это величина, численно равная силе,
действующей со стороны поля на единичный
пробный точечный заряд.
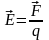 (2), для точечного заряда
(2), для точечного заряда
 (3).
(3).
Графически электрическое поле можно показать с помощью силовой линии – линии, касательной к которой в каждой точке является вектор E. Напряженность поля в каждой точке пропорциональна величине заряда, создающего поле, поэтому, чем больше заряд, тем гуще силовые линии.
Потенциал – это величина, численно
равная потенциальной энергии пробного
единичного положительного точечного
заряда в электрическом поле
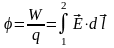 (4), для точечного заряда
(4), для точечного заряда
 (5).
(5).
С помощью формул (3) и (5) может быть рассчитана напряженность поля любого распределения зарядов.
Теорема Гаусса.
П отоком
Ф вектора напряженности Е электрического
поля через поверхность S
называется интеграл от скалярного
произведения
отоком
Ф вектора напряженности Е электрического
поля через поверхность S
называется интеграл от скалярного
произведения
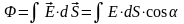 .
Поток вектора Е определяет число силовых
линий электрического поля, пересекающих
выбранную поверхность. Если систему
электрических зарядов окружить замкнутой
поверхностью, то число силовых линий,
пересекающих ее, будет пропорционально
величине заряда, попадающего внутрь
этой поверхности.
.
Поток вектора Е определяет число силовых
линий электрического поля, пересекающих
выбранную поверхность. Если систему
электрических зарядов окружить замкнутой
поверхностью, то число силовых линий,
пересекающих ее, будет пропорционально
величине заряда, попадающего внутрь
этой поверхности.
Теорема Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность прямо пропорционален суммарному заряду, охватываемому этой поверхностью.
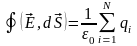 (1)
(1)
Доказательство.
В ыберем
произвольную поверхность, окружающую
N точечных зарядов. Согласно
принципу суперпозиции, напряженность
поля зарядов равна сумме напряженностей
полей, созданных каждым из зарядов.
ыберем
произвольную поверхность, окружающую
N точечных зарядов. Согласно
принципу суперпозиции, напряженность
поля зарядов равна сумме напряженностей
полей, созданных каждым из зарядов.
 ,
тогда поток результирующего вектора
напряженности равен
,
тогда поток результирующего вектора
напряженности равен
 ,
,
 ,
тогда
,
тогда

Применение теоремы Гаусса существенно облегчает расчет напряженностей полей симметричных распределений зарядов.
Диэлектрики во внешнем электрическом поле.
Э
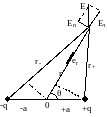 лектрическое
поле диполя. Диполь во внешнем
электрическом поле.
лектрическое
поле диполя. Диполь во внешнем
электрическом поле.
Электрическим диполем называется система двух одинаковых по величине, но разноименно заряженных частиц. Прямая, проходящая через оба заряда, называется осью диполя.
Найдем потенциал и напряженность поля в точке, характеризующейся полярными координатами r и θ, относительно центра диполя. Расстояния от центра диполя до каждого из зарядов равно a, тогда расстояния от зарядов до выбранной точки пространства равно:
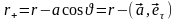

потенциал в точке наблюдения равен
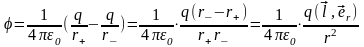 ,
вводя понятие дипольного момента
,
вводя понятие дипольного момента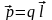 ,
получим
,
получим
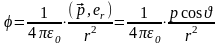 .
.
Для нахождения напряженности поля
найдем производные
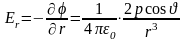 - радиальная составляющая,
- радиальная составляющая,
 ,
тогда
,
тогда

П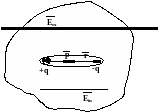 отенциальная
энергия диполя во внешнем поле
отенциальная
энергия диполя во внешнем поле
 ,
вращающий момент, действующий на диполь
,
вращающий момент, действующий на диполь
 .
.
Диэлектрики во внешнем электрическом поле.
Диэлектриками называются вещества, не
способные проводить электрический ток.
В диэлектрике все заряды находятся в
связанном состоянии (положительно
заряженные ядра атомов и отрицательные
электронные оболочки), поэтому при
внесении диэлектрика во внешнее поле
атом поляризуется (приобретает дипольный
момент), и внутреннее поле диэлектрика
определяется суммарным дипольным
моментом его атомов
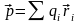 .
.
Э лектроны
движутся с огромными скоростями, поэтому
дипольный момент атома на практике
определяется средним значением
радиус-вектора
лектроны
движутся с огромными скоростями, поэтому
дипольный момент атома на практике
определяется средним значением
радиус-вектора
 .
У симметричных молекул, таких как Н2,
О2, N2 в отсутствии
внешнего поля центры тяжести положительного
и отрицательного зарядов совпадают,
поэтому они не обладают собственным
дипольным моментом и называются
неполярными. У несимметричных
молекул, таких как СО, NH,
HCl, центры тяжести
положительных и отрицательных зарядов
в отсутствии внешнего поля не совпадают
и молекулы обладают собственным дипольным
моментом и называются полярными. Под
действием внешнего поля заряды неполярной
молекулы смещаются друг относительно
друга: положительный по полю, отрицательный
– против поля и молекула приобретает
дипольный момент, величина которого
пропорциональна напряженности внешнего
поля
.
У симметричных молекул, таких как Н2,
О2, N2 в отсутствии
внешнего поля центры тяжести положительного
и отрицательного зарядов совпадают,
поэтому они не обладают собственным
дипольным моментом и называются
неполярными. У несимметричных
молекул, таких как СО, NH,
HCl, центры тяжести
положительных и отрицательных зарядов
в отсутствии внешнего поля не совпадают
и молекулы обладают собственным дипольным
моментом и называются полярными. Под
действием внешнего поля заряды неполярной
молекулы смещаются друг относительно
друга: положительный по полю, отрицательный
– против поля и молекула приобретает
дипольный момент, величина которого
пропорциональна напряженности внешнего
поля
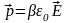 .
Здесь β – поляризуемость молекулы.
Действие внешнего поля на полярную
молекулу сводится к стремлению повернуть
молекулу так, чтобы ее дипольный момент
выровнялся по направлению внешнего
поля.
.
Здесь β – поляризуемость молекулы.
Действие внешнего поля на полярную
молекулу сводится к стремлению повернуть
молекулу так, чтобы ее дипольный момент
выровнялся по направлению внешнего
поля.
Поляризация диэлектриков.
Чтобы охарактеризовать поляризацию
диэлектрика в данной точке, введем
дипольный момент единицы объема
диэлектрика и назовем его поляризованностью
диэлектрика
 - у изотропных диэлектриков
поляризованность
пропорциональна напряженности внешнего
поля. Коэффициент пропорциональности
называется диэлектрической восприимчивостью
χ. Для неполярных диэлектриков
- у изотропных диэлектриков
поляризованность
пропорциональна напряженности внешнего
поля. Коэффициент пропорциональности
называется диэлектрической восприимчивостью
χ. Для неполярных диэлектриков
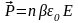 ,
где n – концентрация
молекул, тогда
,
где n – концентрация
молекул, тогда
 .
Для полярных диэлектриков тепловое
движение стремится хаотически
ориентировать дипольные моменты молекул
и в результате устанавливается
преимущественное направление дипольных
моментов, совпадающее с направлением
внешнего поля. Диэлектрическая
восприимчивость таких молекул обратно
пропорциональна их температуре.
.
Для полярных диэлектриков тепловое
движение стремится хаотически
ориентировать дипольные моменты молекул
и в результате устанавливается
преимущественное направление дипольных
моментов, совпадающее с направлением
внешнего поля. Диэлектрическая
восприимчивость таких молекул обратно
пропорциональна их температуре.
Поле внутри диэлектрика представляет
собой суперпозицию внешнего Eex
или стороннего поля и внутреннего Ein
или поля связанных зарядов, созданного
поляризованными молекулами
 .
.
П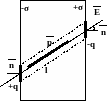 оверхностная
плотность связанных зарядов определяется
поляризованностью диэлектрика. Рассмотрим
бесконечную диэлектрическую пластину,
поляризованную так, что одна ее плоскость
имеет поверхностную плотность заряда
+σ, а другая –σ. Выделим внутри пластины
цилиндр, ось которого совпадает с
направлением внешнего поля, тогда
дипольный момент такой системы
оверхностная
плотность связанных зарядов определяется
поляризованностью диэлектрика. Рассмотрим
бесконечную диэлектрическую пластину,
поляризованную так, что одна ее плоскость
имеет поверхностную плотность заряда
+σ, а другая –σ. Выделим внутри пластины
цилиндр, ось которого совпадает с
направлением внешнего поля, тогда
дипольный момент такой системы
 ,
с другой стороны, дипольный момент равен
,
с другой стороны, дипольный момент равен
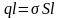 ,
тогда
,
тогда
 .
Или, используя связь с напряженностью
поля внутри диэлектрика,
.
Или, используя связь с напряженностью
поля внутри диэлектрика,

Аналогично, связанные заряды, переносимые
через воображаемую площадку dS
внутри неоднородного диэлектрика,
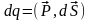 ,
тогда представив внутри диэлектрика
замкнутую поверхность получим связанный
заряд, пересекающий ее под действием
поляризации
,
тогда представив внутри диэлектрика
замкнутую поверхность получим связанный
заряд, пересекающий ее под действием
поляризации
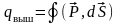 ,
в результате, в объеме, ограниченном
поверхностью, возникает избыточный
заряд, равный
,
в результате, в объеме, ограниченном
поверхностью, возникает избыточный
заряд, равный
 ,
вводя объемную плотность связанных
зарядов, можно записать
,
вводя объемную плотность связанных
зарядов, можно записать
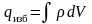 .
По теореме Гаусса
.
По теореме Гаусса
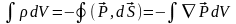 ,
тогда объемная плотность связанных
зарядов в диэлектрике равна
,
тогда объемная плотность связанных
зарядов в диэлектрике равна
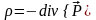 .
Связанные заряды отличаются от сторонних
только тем, что не могут покидать свои
места под действием внешнего поля, а в
остальном, они ведут себя как сторонний
заряды, в частности, создают электрическое
поле, поэтому, напряженность поля внутри
диэлектрика определяется объемной
плотностью как сторонних, так и связанных
зарядов.
.
Связанные заряды отличаются от сторонних
только тем, что не могут покидать свои
места под действием внешнего поля, а в
остальном, они ведут себя как сторонний
заряды, в частности, создают электрическое
поле, поэтому, напряженность поля внутри
диэлектрика определяется объемной
плотностью как сторонних, так и связанных
зарядов.
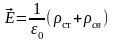 ,
тогда, учитывая, что
,
тогда, учитывая, что
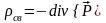 ,
получим,
,
получим,
 .
Введем вектор электрического смещения
(электрическую индукцию)
.
Введем вектор электрического смещения
(электрическую индукцию)
 ,
где ε0 – диэлектрическая
проницаемость диэлектрика.
,
где ε0 – диэлектрическая
проницаемость диэлектрика.
Условия на границе раздела двух диэлектриков.
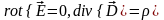
Р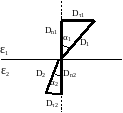 ассмотрим
границу раздела двух диэлектриков,
вдоль которой циркулирует вектор E.В
качестве контура выбираем прямоугольник,
две стороны которого параллельны границе
раздела, а высота бесконечно мала, тогда
Eτ1=Eτ2,
с учетом соотношения для E
и D, получим
ассмотрим
границу раздела двух диэлектриков,
вдоль которой циркулирует вектор E.В
качестве контура выбираем прямоугольник,
две стороны которого параллельны границе
раздела, а высота бесконечно мала, тогда
Eτ1=Eτ2,
с учетом соотношения для E
и D, получим
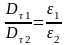 .
.
Если на границе раздела нет сторонних
зарядов, то согласно теореме Гаусса
поток через замкнутую поверхность будет
равен нулю, тогда Dn1=Dn2
и
 и
и

