Обчислення значення критерію Пірсона
Xі |
ni |
p'(X)=p(X)n |
ni-p'(X) |
(ni-p'(X))^2 |
χ2спос=(ni-p'(X))^2/p'(x) |
257,50 |
2 |
1,43 |
0,57 |
0,33 |
0,23 |
264,50 |
2 |
2,94 |
-0,94 |
0,89 |
0,30 |
271,50 |
8 |
5,04 |
2,96 |
8,74 |
1,73 |
278,50 |
7 |
7,18 |
-0,18 |
0,03 |
0,00 |
285,50 |
9 |
8,49 |
0,51 |
0,27 |
0,03 |
292,50 |
5 |
8,33 |
-3,33 |
11,08 |
1,33 |
299,50 |
6 |
6,79 |
-0,79 |
0,62 |
0,09 |
306,50 |
6 |
4,60 |
1,40 |
1,97 |
0,43 |
313,50 |
3 |
2,58 |
0,42 |
0,17 |
0,07 |
320,50 |
2 |
1,21 |
0,79 |
0,63 |
0,52 |
|
50 |
|
|
Еχ2спос |
4,739619006 |
оскільки визначене за результатами спостережень значення критерію не перевищує критичну точку
<
,
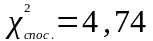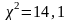робимо висновок, що є
підстави прийняти гіпотезу про
нормальний розподіл випадкової
величини, тобто досвідна і теоретична
частоти не відрізняються
значним чином. Отже, гіпотеза про
нормальність прийнята.
5. Операції з нормальним розподілом
Функція нормального розподілу визначається інтегруванням густини і може бути легко розрахована за допомогою табульованих функцій Лапласа:
|
|
(1.5) |
Знак плюс відповідає позитивному значенню нормованого відхилення, знак мінус - негативному значенню.
|
|
(1.6) |
.Визначимо для прикладу ймовірність попадання випадкової величини, що розглядається у прикладі, в інтервал 248,21< x < 328,21.
Визначимо нормовані аргументи:
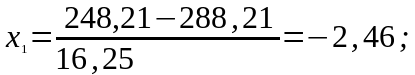
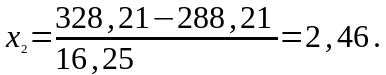
Значення функції Лапласа:
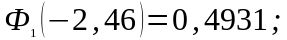
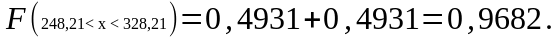
Таким
чином, вихід випадкової величини за
межі
має ймовірність 0,27%,
тобто є практично неможливим (правило
“трьох сигма”).
Нормативне значення межі текучості сталі із забезпеченістю 0,95:
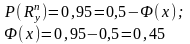
При Ф(х)=0,45 х=1,65.
Таким чином, за допомогою функції Лапласа, отримаємо нормативний опір сталі на розтяг для заданої вибірки випробування сталевих зразків на розтяг:
Нормативний опір сталі на розтяг:
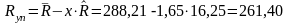мПа
Розрахунковий опір сталі на розтяг:
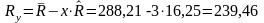мПа
ПолтНТУ, Кафедра конструкцій з металу дерева ы пластмасс
ідпи
мн.
с а
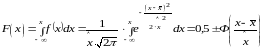
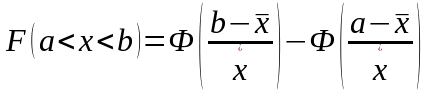