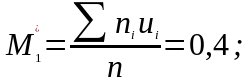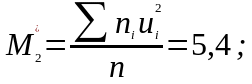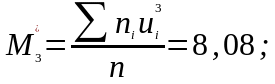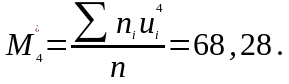- •Розрахунково-графічна робота № 1
- •Визначення нормативного і розрахункового опору сталі на розтяг
- •Побудова експериментального полігону розподілу
- •2. Визначення вибіркових числових характеристик
- •3. Підбір нормального розподілу
- •Підбір ординат нормального розподілу
- •4. Перевірка відповідності експериментального розподілу нормальному
- •Обчислення значення критерію Пірсона
- •5. Операції з нормальним розподілом

Розрахунково-графічна робота № 1
Варіант № 69
Визначення нормативного і розрахункового опору сталі на розтяг
Побудова експериментального полігону розподілу
Вихідні дані-вибірка даних випробування сталевих зразків на розтяг, МПа.
Вихідні дані. Вибірка даних випробувань загальним обсягом n = 50:
306,4 |
301,3 |
286,5 |
282,1 |
303,2 |
312,2 |
309,6 |
277,2 |
291,1 |
294,9 |
255,3 |
288,7 |
271,1 |
280,1 |
316 |
282,4 |
276,6 |
300 |
294,9 |
289 |
285,4 |
296,8 |
268,2 |
291 |
286,6 |
304,2 |
266 |
304,5 |
274,5 |
269,3 |
321,4 |
254,3 |
288,1 |
277,5 |
274,1 |
273,9 |
299,2 |
282,1 |
301 |
322,3 |
310,2 |
305,7 |
278,7 |
280,1 |
278,3 |
273,1 |
273,6 |
290,7 |
296,2 |
264,9 |
Побудова експериментального полігону виконується у такій послідовності (див. табл. 1.1):
· діапазон можливих значень випадкової величини (різниця між найбільшим та найменшим значенням у вибірці) поділяється на 8-12 рівних інтервалів із середніми значеннями хі (стовпчик 1 табл. 1.1);
· підраховується
кількість попадань ВВ
 у кожний інтервал, причому
у кожний інтервал, причому
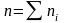 (стовпчик
2);
(стовпчик
2);
· підраховуються експериментальні частоти попадання ВВ у кожний інтервал (у тому числі значення, що дорівнюють нижній межі інтервалу)
|
|
( 1.1 ), |
причому
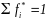 .
Підрахунки частот можуть виконуватися
у відсотках, тоді
.
Підрахунки частот можуть виконуватися
у відсотках, тоді
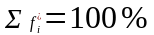 .
Числові значення частот наведеної вище
вибірки подані у стовпчику 3 табл. 1.2;
.
Числові значення частот наведеної вище
вибірки подані у стовпчику 3 табл. 1.2;
· будується експериментальний полігон розподілу випадкової величини (рис.1.13).
2. Визначення вибіркових числових характеристик
Обчислення виконуються методом добутків у таблиці 1.1.
Таблиця 1.1
Межі інтервалів |
xi |
ni |
fi |
ui |
ni*ui |
ni*ui^2 |
ni*ui^3 |
ni*ui^4 |
ni*(ui+1)^4 |
|
254 |
261 |
257,5 |
2 |
0,04 |
-4 |
-8 |
32 |
-128 |
512 |
162 |
261 |
268 |
264,5 |
2 |
0,04 |
-3 |
-6 |
18 |
-54 |
162 |
32 |
268 |
275 |
271,5 |
8 |
0,16 |
-2 |
-16 |
32 |
-64 |
128 |
8 |
275 |
282 |
278,5 |
7 |
0,14 |
-1 |
-7 |
7 |
-7 |
7 |
0 |
282 |
289 |
285,5 |
9 |
0,18 |
0 |
0 |
0 |
0 |
0 |
9 |
289 |
296 |
292,5 |
5 |
0,1 |
1 |
5 |
5 |
5 |
5 |
80 |
296 |
303 |
299,5 |
6 |
0,12 |
2 |
12 |
24 |
48 |
96 |
486 |
303 |
310 |
306,5 |
6 |
0,12 |
3 |
18 |
54 |
162 |
486 |
1536 |
310 |
317 |
313,5 |
3 |
0,06 |
4 |
12 |
48 |
192 |
768 |
1875 |
317 |
324 |
320,5 |
2 |
0,04 |
5 |
10 |
50 |
250 |
1250 |
2592 |
|
|
Сума |
50 |
1 |
|
20 |
270 |
404 |
3414 |
6780 |
Пояснення до таблиці 1.1:
· для спрощення розрахунків вибраний “умовний нуль” С=285,5, що відповідає значенню хі з максимальною частотою, та підраховані умовні варіанти uі;
· виконується контроль обчислень
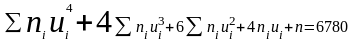
що збігається зі сумарним значенням у стовпчику 9 табл. 1.2.
Визначаються умовні моменти 1-4 порядків:
|
|
|
|
Вибіркові числові характеристики дорівнюють:
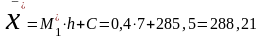 МПа
– математичне очікування;
МПа
– математичне очікування;
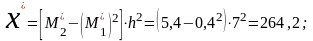
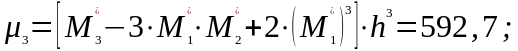
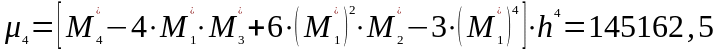 ;
;
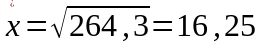 МПа –
стандарт;
МПа –
стандарт;
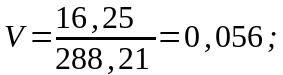 – коефіцієнт
варіації;
– коефіцієнт
варіації;
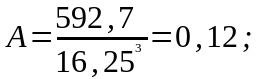 –
коефіцієнт
асиметрії;
–
коефіцієнт
асиметрії;
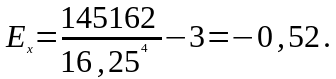 –
ексцес.
–
ексцес.

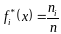 ,
,