
- •I Элементы линейной алгебры.
- •Матрицы и определители. Векторная алгебра (а).
- •Аналитическая геометрия. (a)
- •3. Введение математического анализа. Функция. Предел и непрерывность (а) (b).
- •4. Производная функции одной переменной и ее приложения (а) (в).
- •Комплексные числа и операции над ними. (а) (в).
- •7. Определенный интеграл и несобственные интегралы. (а) (в).
- •Какие из этих формул написаны правильно?
- •Какие из этих формул написаны правильно?
Комплексные числа и операции над ними. (а) (в).
Какое из выражений является тригонометрической формы комплексного числа
 .
.
1).
![]() ,
,
2).![]() ,
,
3)
![]() ,
,
4).
![]() ,
5).
,
5).
![]()
A). 1, B).2, C)3, D) 4, E) 5.
Сколько выражений для данных комплексных чисел верны?
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
,
4)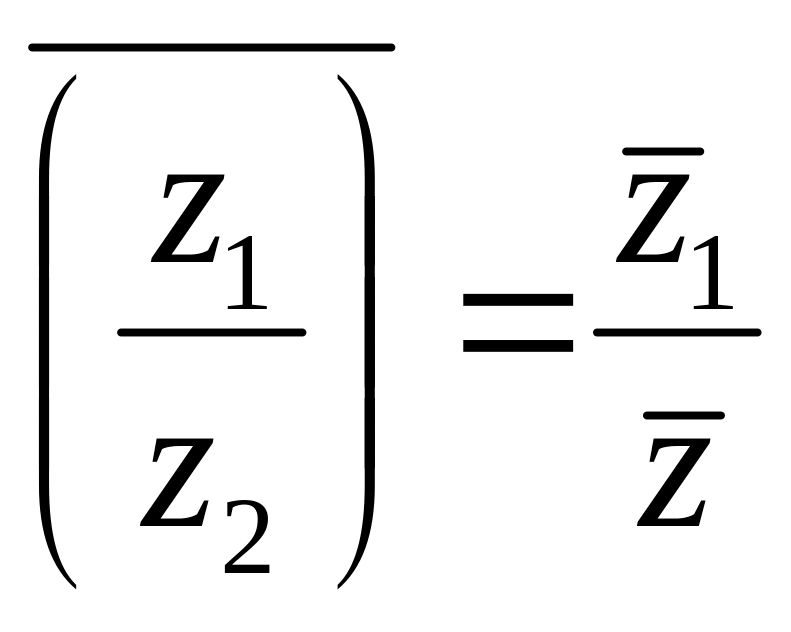 , 5)
, 5)![]()
A)1, B)2, C)3, D)4, E)5
Сколько выражений для данных комплексных чисел верны?
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)![]()
A) 1, B)2, C)3, D)4, E)5
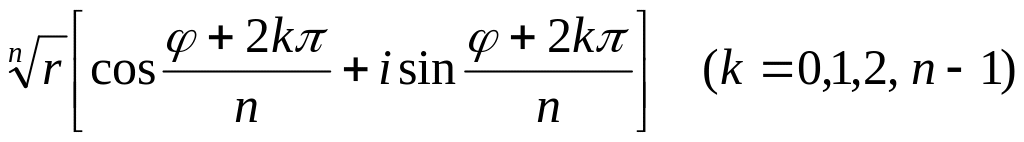 характеризует:
характеризует:
A) Тригонометрическую форму комплексного числа, B)Модуль комплексного числа, C)Аргумент комплексного числа, D)Корень -ой степени из комплексного числа, заданного в тригонометрической форме, E) Аргумент сопряженного комплексного числа.
Если
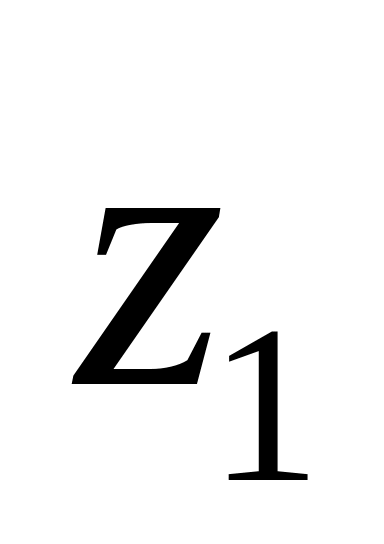 и
и
 комплексные
числа, то выражение
комплексные
числа, то выражение
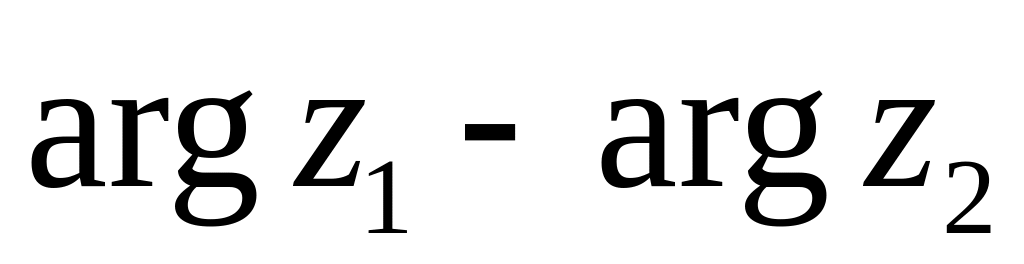 характеризует:
характеризует:
A)Аргумент отношения двух комплексных чисел, B) Аргумент произведения двух комплексных чисел, C)Разность модулей двух комплексных чисел, D)Сумма модулей двух комплексных чисел, E)Сумма квадратов двух комплексных чисел.
Если задаются комплексные числа
 и
и
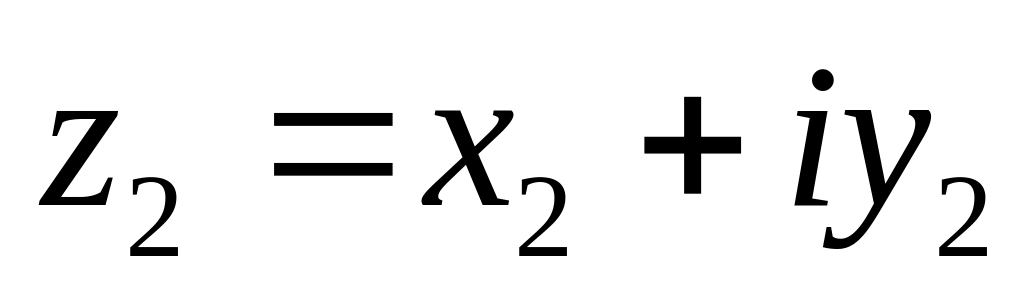 то,
выражение
то,
выражение
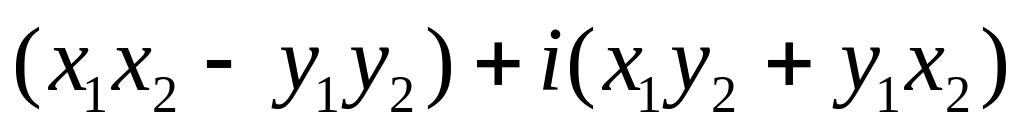 характеризует:
характеризует:
A. Отношение двух комплексных чисел, B. Сумму квадратов двух комплексных чисел, C. Произведению двух комплексных чисел,
D. Разность модулей двух комплексных чисел,
E.Сумму модулей двух комплексных чисел.
Если даны и то, выражение
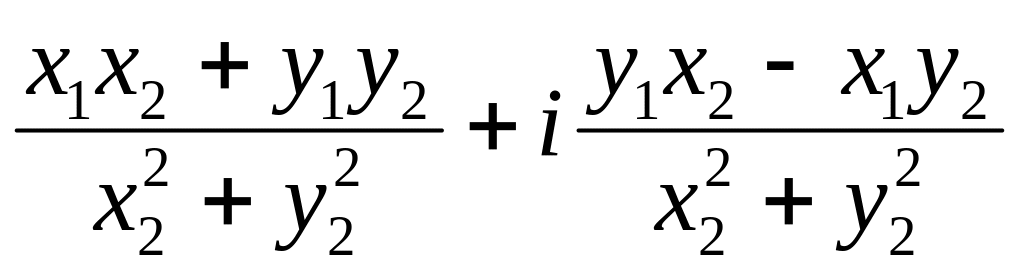 характеризует:
характеризует:
A. Отношение двух комплексных чисел,
B. Произведению двух комплексных чисел,
C. Сумму квадратов двух комплексных чисе,
D. Разность квадратов двух комплексных чисел,
E. Произведение модулей двух комплексных чисел.
Используя формулу Муавра вычислить значение
 :
:
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]()
D)
![]() ,
E)
,
E)
![]()
Используя формулу Муавра вычислить значение
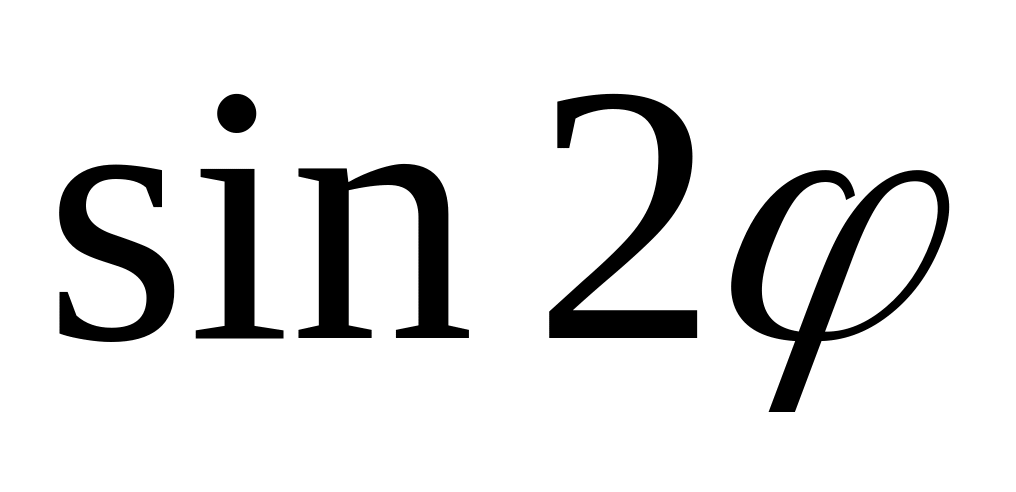 :
:
A)![]() ,
B)
,
B)
![]() ,
C.
,
C.
![]() ,D)
,D)
![]() ,
,
E)
![]()
Как определяется модуль комплексного числа
 .
.
A)![]() ,
B)
,
B)![]() ,C)
,C)
![]() ,
,
D)
![]() ,E)
,E)![]()
 выражает:
выражает:
A)![]() ,
B)
,
B)![]() ,
C)
,
C)
![]()
D)
![]() ,E)
,E)![]() .
.
Задачи Комплексные числа и их свойства (В).
Найти тригонометрическую форму комплексного числа
 :
:
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
,
D)
![]() ,
E)
,
E)
![]()
Найти аргумент комплексного числа
 :
:
A)
0, B)
,
C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
Найти значение выражения
 :
:
A)
![]() ,
B)
,
B)
![]() ,
C)
4, D) -4, E)
,
C)
4, D) -4, E)
![]()
Найти коэффициент при мнимой части комплексного выражения
 :
:
A)
![]() ,
B)
,
C) 1, D)
,
E)
,
B)
,
C) 1, D)
,
E)
![]()
Найти действительную часть
 ,
если
,
если
 и
и
 :
:
A) 4, B) 5, C) 6, D) 7, E) 8
Найти тригонометрическую форму комплексного числа
 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
,
D)
![]() ,
E)
,
E)
![]()
Вычислить
 .
.
A)
1, B)
![]() ,
C)
,
D)
,
E)
,
C)
,
D)
,
E)
![]()
Вычислить
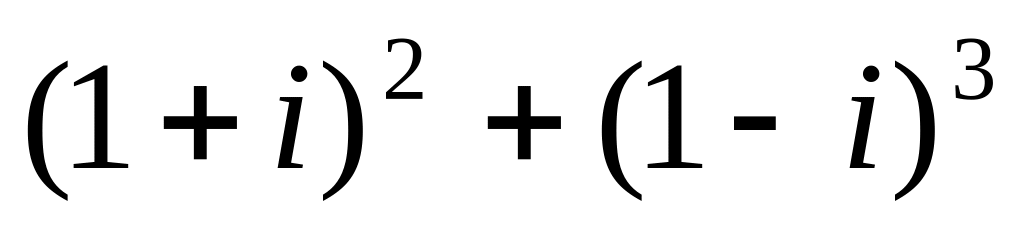 .
.
A)
8, B)
![]() ,
C) 2, D) -
,
E)
-2
,
C) 2, D) -
,
E)
-2
Дана
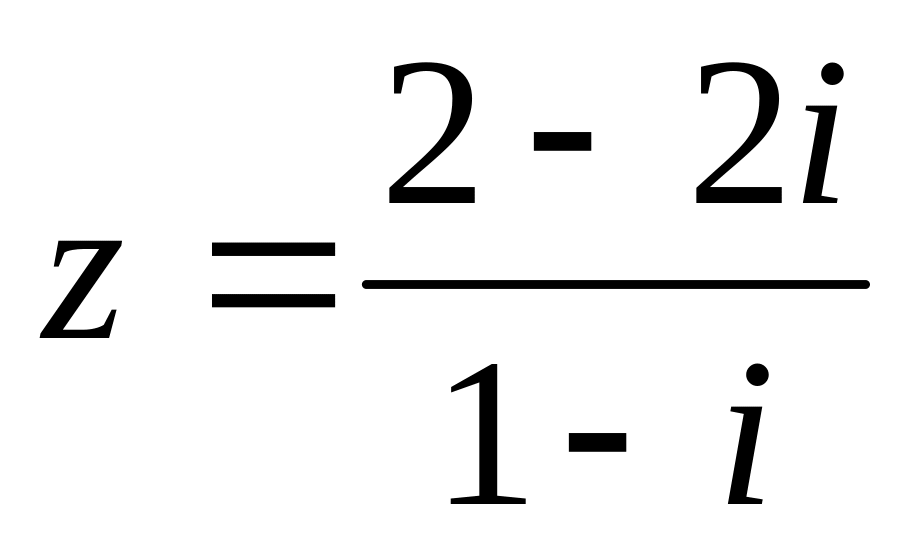 ,
найти ее действительную часть:
,
найти ее действительную часть:
A) -1, B) 0, C) 1, D) 2, E)
Если
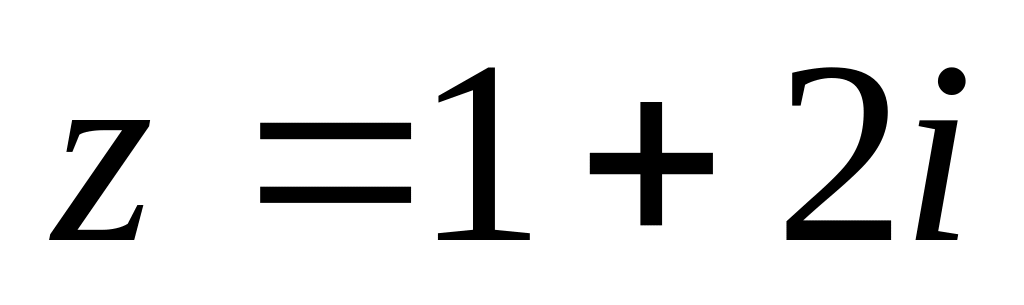 ,
то чему равен
,
то чему равен
 ?
?
A)
,
B)
,
C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
Найти действительную часть выражения
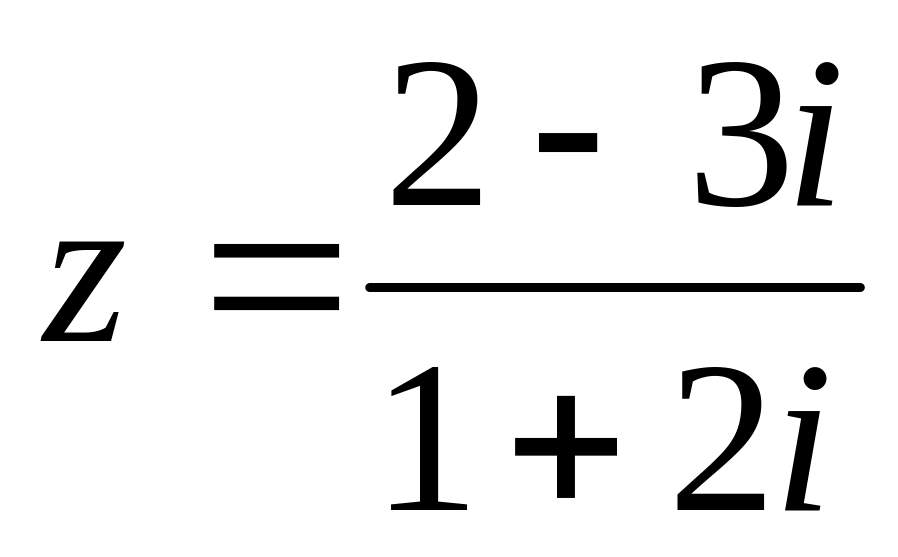 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
D)
,
C)
,
D)
![]() ,
E)
,
E)
![]()
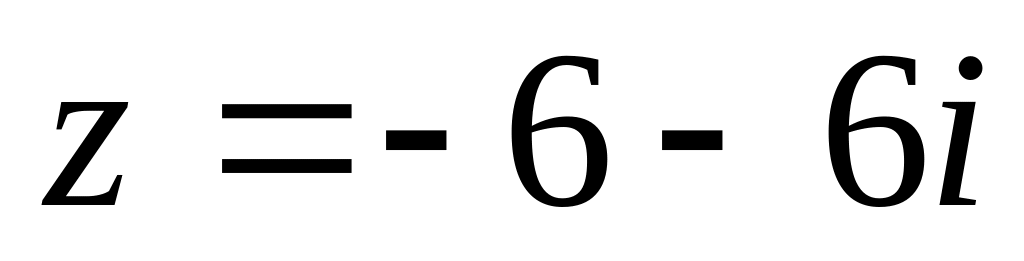 ,
найти
,
найти
 .
.
A)
36, B) -36, C) 6, D)
![]() ,
E) 12
,
E) 12
Написать в тригонометрической форме число
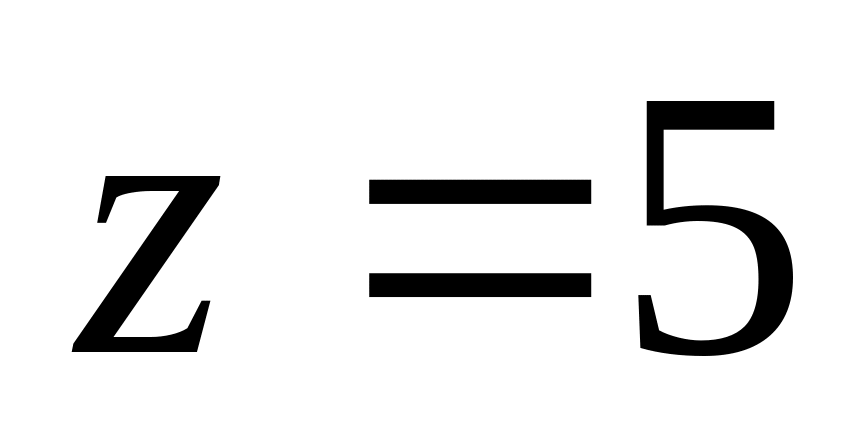 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
![]()
Написать в тригонометрической форме число
 .
.
A)
![]() ,
B)
,
C)
,
,
B)
,
C)
,
D)
![]() ,
E)
,
E)
![]()
Найти модуль комплексного числа
 .
.
A)
![]() ,
B)
2, C) 1, D)
,
E)
,
B)
2, C) 1, D)
,
E)
![]()
Найти модуль комплексного числа
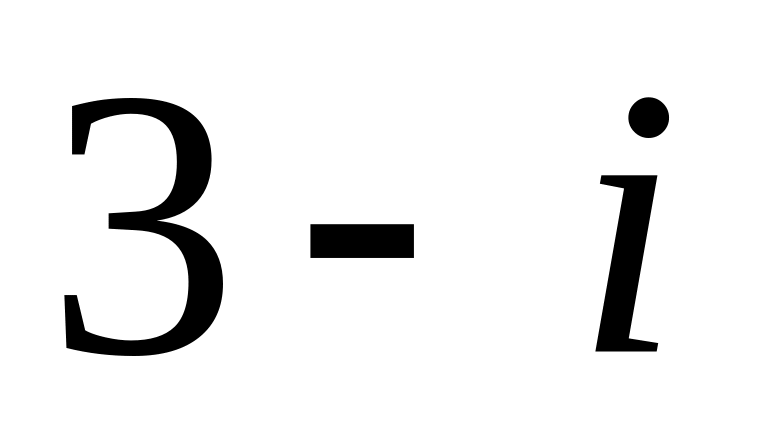 .
.
A)
3, B)-1, C)
![]() ,
D)
,
D)
![]() ,
E) 0
,
E) 0
Написать в тригонометрической форме комплексного числа
 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]()
D)
![]() ,
E)
,
E)
![]() 2
2
Найти аргумент комплексного числа .
A) 0, B) , C) , D) , E)
19. Вычислить
![]() .
.
A) 4, B)-4, C) 4 , D)-4 , E)2
20.
Используя формулу Муавра вычислить
![]() .
.
A) 1, B) -1, C) , D) – , E) 2
21.
Вычислить![]() .
.
A)
-1, B)
1, C)
,
D)-
, E)![]()
Комплексные числа (B)
Вычислить
 (добавка)
(добавка)
A.2i, B.5, C. , D.-4, E. -2i
Вычислить

A.![]() ,
B.
,
B.
![]() ,
C.
,
C.
![]() ,
D.
,
D.![]() ,
E.
,
E.![]() .
.
Найти модуль комплексного числа
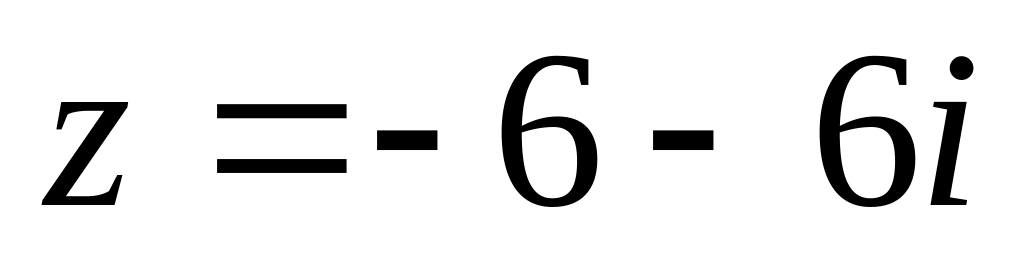
A.36, B. , C.6, D.-3,6, E.12
Найти
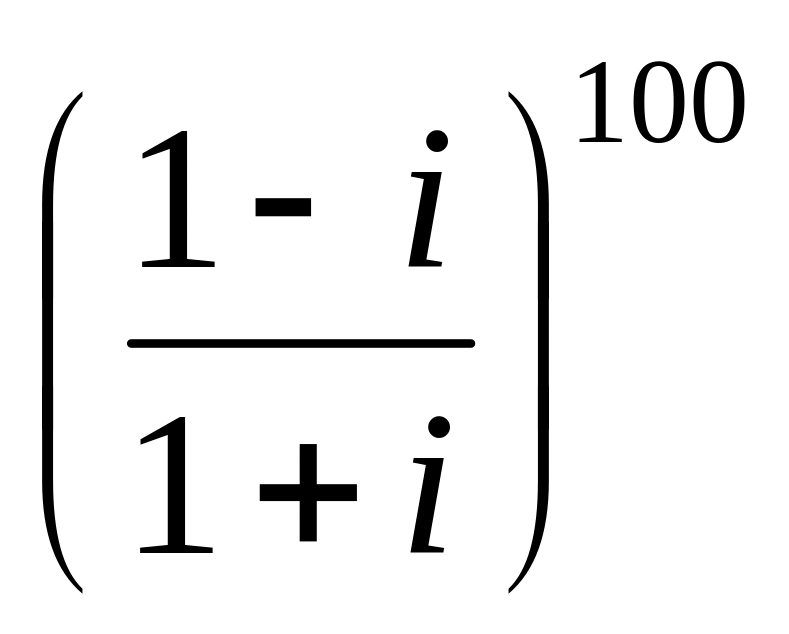
A.
i,
B.1,
C.-1, D.![]() ,
E.-i
,
E.-i
Вычислить

A.16, B.32i, C.-32i, D.16i, E.12.
Неопределенный интеграл. (А) (В).
Какие из этих выражений написано правильно?
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() 5)
5)
![]() .
.
А) 1,3,4 В) 1,2,5 С) 1,2,4,5 D) 1,2,3,4,5 E) 1,5.
Какое из этих выражений написано неправильно?
А)![]() В)
В)![]() С)
С)![]()
D)![]() ;
E)
;
E)![]() .
.
Какое из этих выражений представляет формулу интегрирования по частям?
А)![]() В)
В)![]() ;
С)
;
С)![]()
D)
E)![]() ,
где
постоянная.
,
где
постоянная.
Показать формулу замены переменной в неопределенном интеграле:
А) В) С)
D) E) .
Покажите формулу, выражающий определение неопределенного интеграла:
А) В) С)
D) E) .
Какое из этих выражений написано неправильно?
А)
В)
![]() ;
С)
;
;
С)
;
D) Е) .
Какие из этих табличных интегралов написаны правильно?
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
;
4)
![]() ;
5)
.
;
5)
.
А) 1,3,5 В) 3,4,5 С) 2,3,5 D) 1,2,3,4,5 E) 1,4.
Какие из этих табличных интегралов написаны неправильно?
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
;
4)
![]() ;
5)
.
;
5)
.
А) 2,4, В) 1,2,3 С) 1,2,3,4,5 D) 1,5,4 E) 1,3,5.
Какое из этих выражений написано неправильно?
А)![]() В)
В)![]() С)
С)
D)![]() ;
E)
.
;
E)
.
Какое из этих интегралов интегрируется с помощью подстановки
 ?
?
А)![]() В)
В)![]() С)
С)![]()
D)![]() ;
E)
;
E)![]() .
.
Какое из этих интегралов, интегрируется с помощью подставки

А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Среди этих выражений найдите рекуррентную формулу?
А)![]() В)
В)![]()
С)![]()

E)![]() .
.
Неопределенные интегралы. Задачи (В).
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)
![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Найти интеграл:

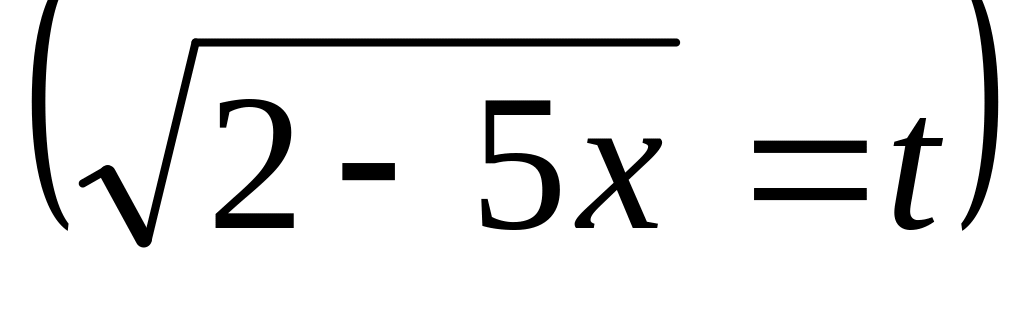
А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:
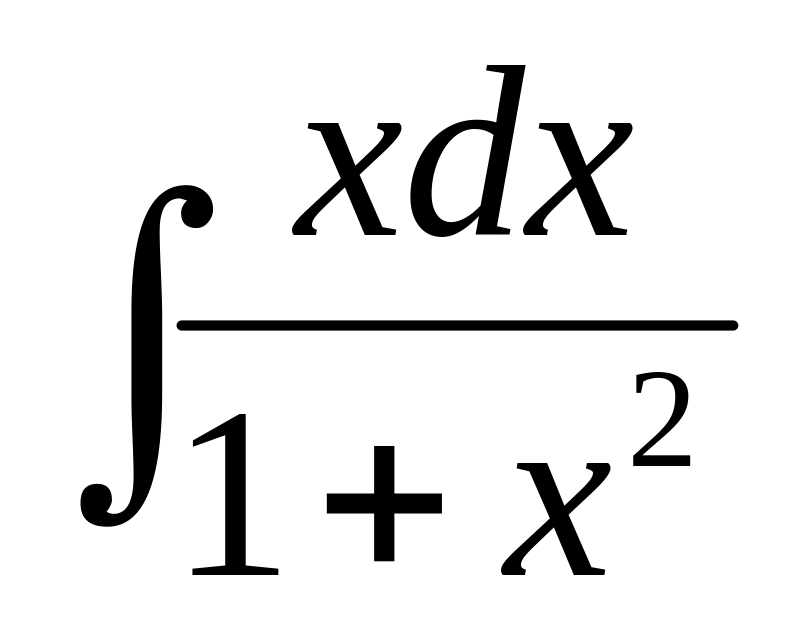
А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)
![]()
D)
![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:
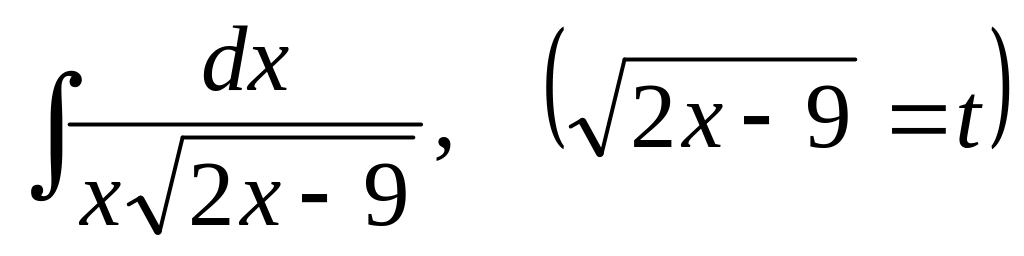
А)
![]() В)
В)
![]() С)
С)![]()
D)
![]() E)
E)
![]() .
.
Найти интеграл:
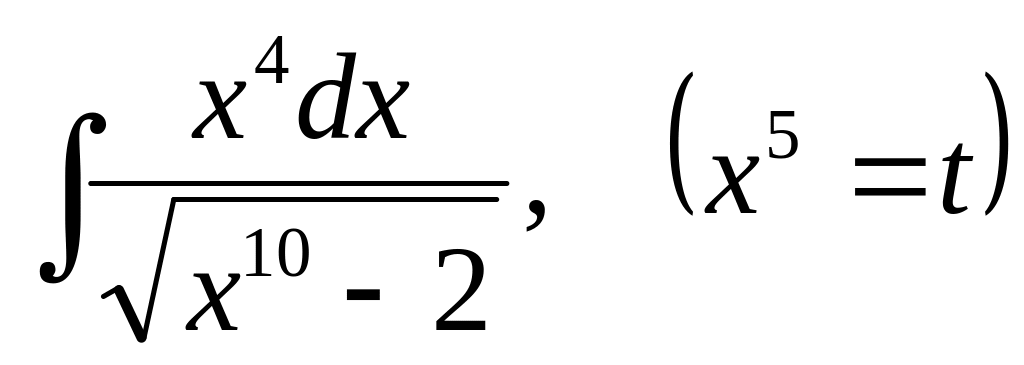
А)
![]() В)
В)
![]() С)
С)
![]()
D)
![]() E)
E)
![]() .
.
Найти интеграл:

А)
![]() В)
В)
![]() С)
С)
![]()
D)
![]() E)
E)![]() .
.
Найти интеграл:

А)
![]() В)
В)
![]() С)
С)
![]()
D)
![]() E)
E)
![]() .
.
Найти интеграл:
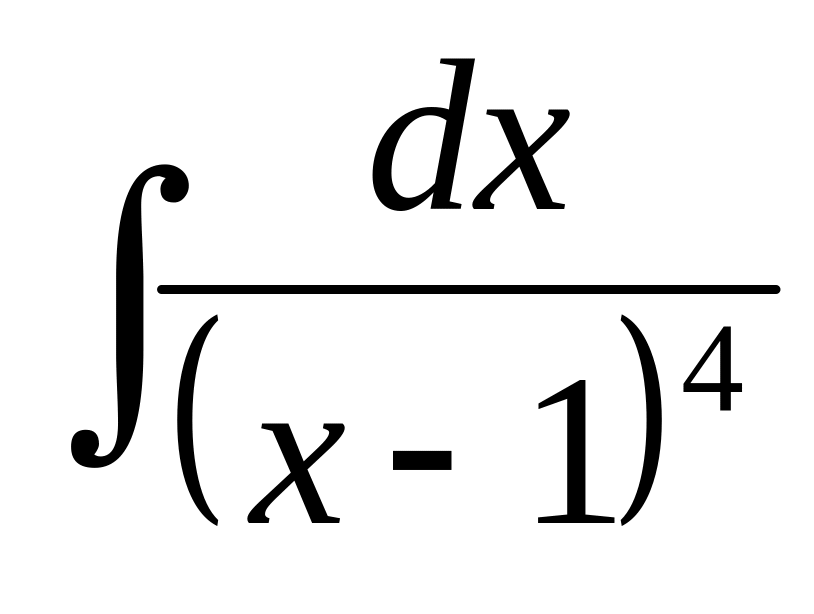
А)![]() В)
В)
![]() С)
С)![]()
D)![]() E)
E)
![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]() D)
D)![]() E)
E)![]() .
.
Найти интеграл:

А)![]() В)
В)![]() С)
С)![]()
D)![]() E)
E)![]() .
.
Найти интеграл:
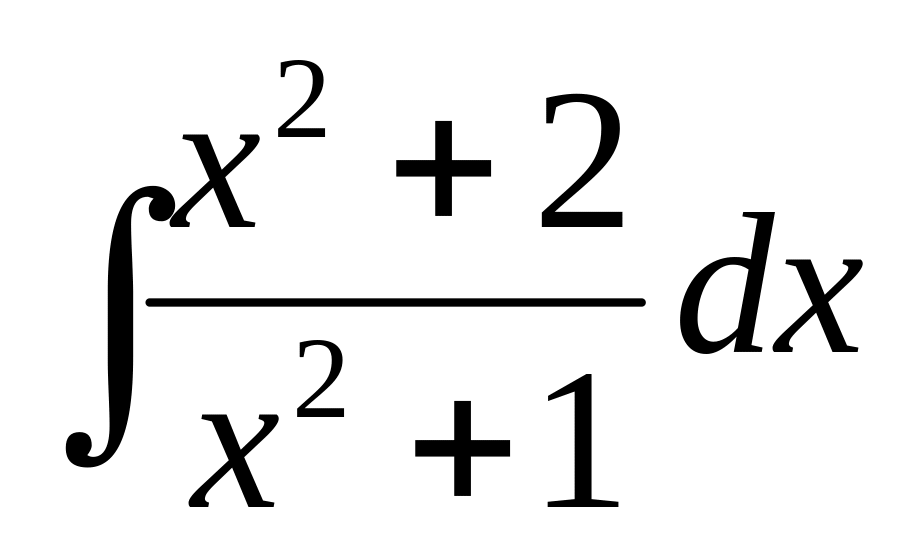
А)
![]() В)
В)
![]() С)
С)![]()
D)
![]() E)
E)
![]() .
.
Найти интеграл:
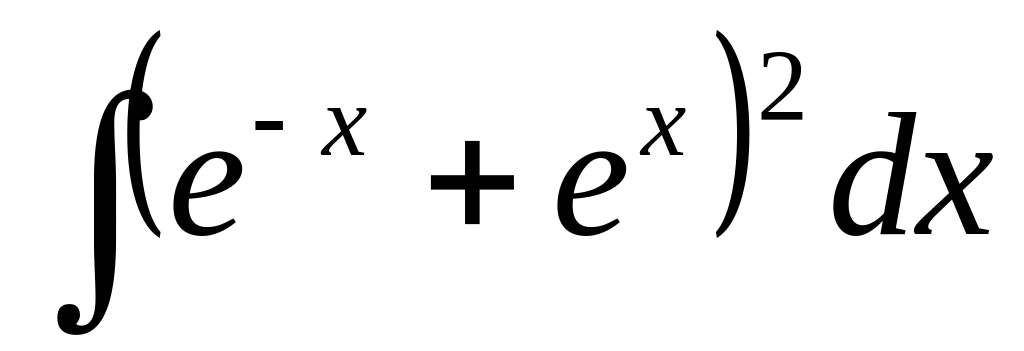
А)![]() В)
В)![]() С)
С)
![]()
D)
![]() E)
E)
![]() .
.
Неопределенные интегралы (В). (6) (новая добавка)
21. Найти интеграл:
![]()
А)
![]() В)
В)
![]() С)
С)
![]()
Д)![]() Е)
Е)
![]()
22. Найти интеграл:
![]()
А)
![]() В)
В)
![]()
С)
![]() Д)
Д)
![]() Е)
Е)
![]()
23. Найти интеграл
![]() :
:
А)
![]() В)
В)
![]() С)
С)
![]()
Д)
![]() Е)
Е)
![]()
Найти интеграл:
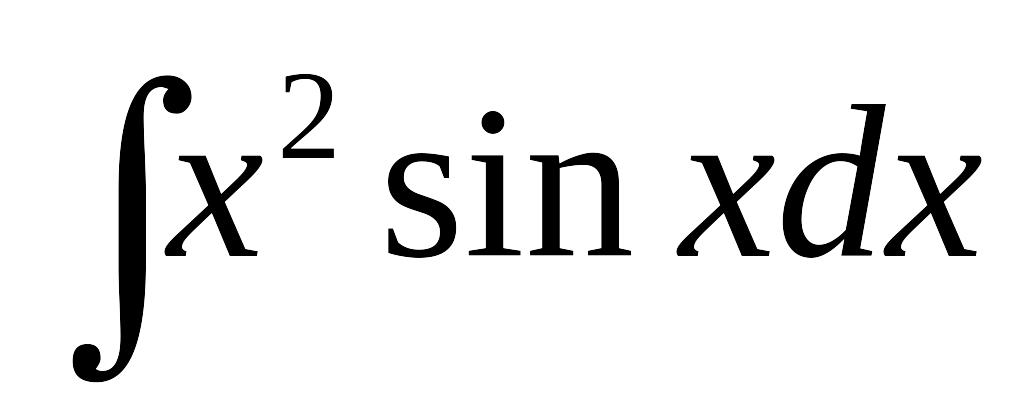 .
.
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
Найти интеграл:
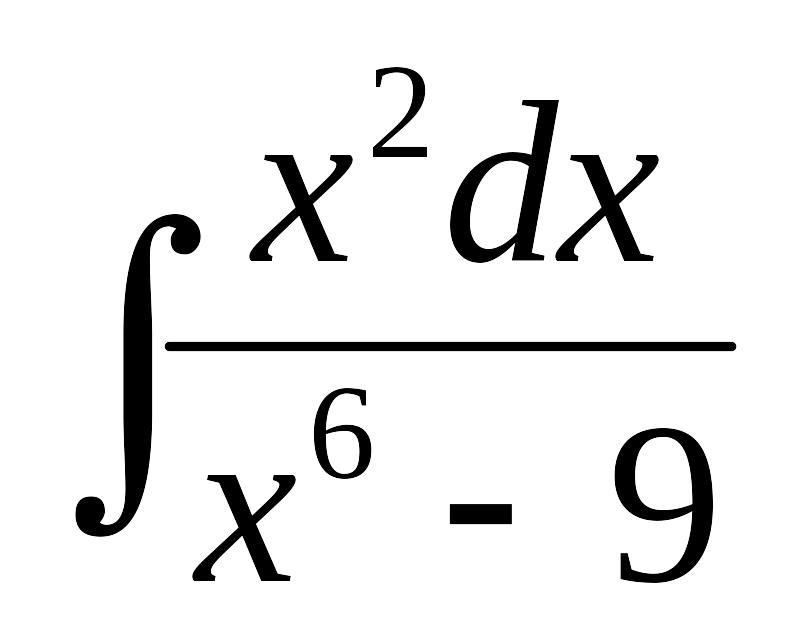 .
.
А)
![]() В)
В)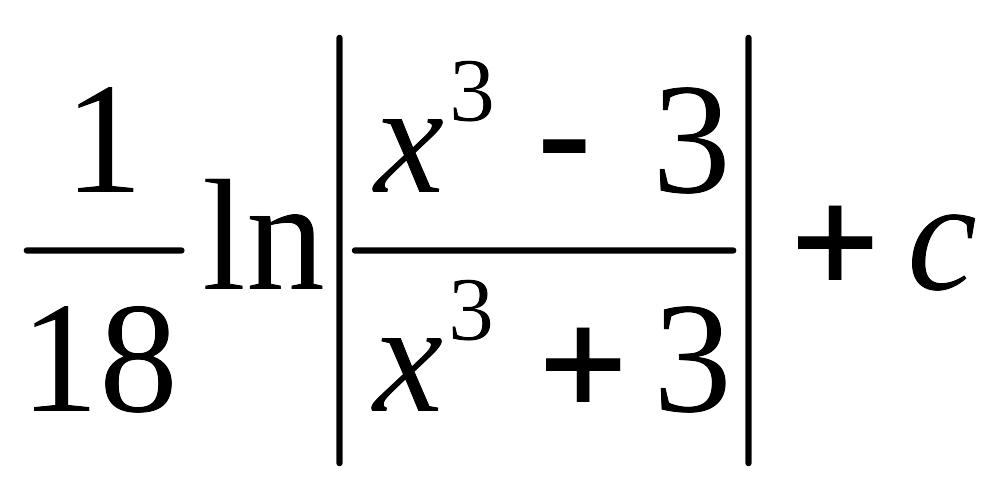 С)
С)
![]()
Д)
![]() Е)
Е)
![]()
Найти интеграл:
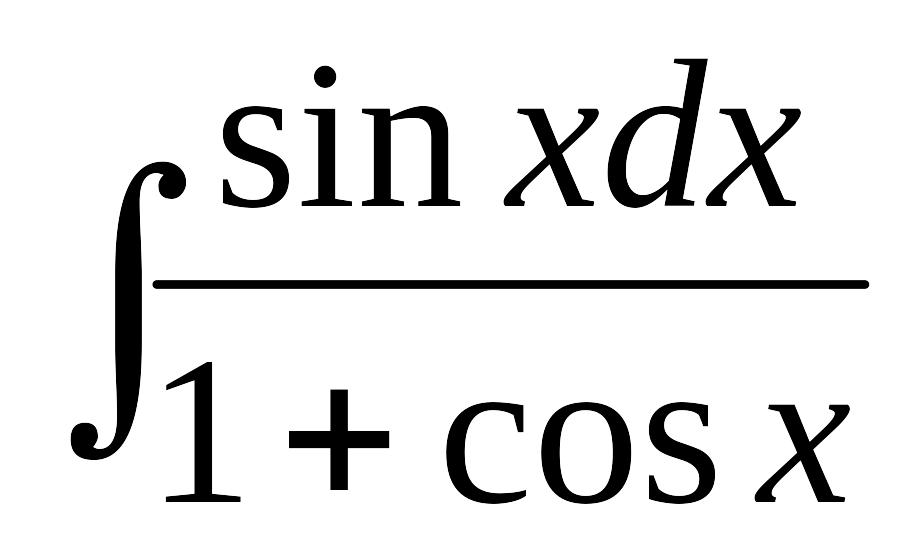 .
.
А)
![]() В)
В)
![]() С)
С)![]()
Д)
![]() Е)
Е)
![]()
Найти интеграл:
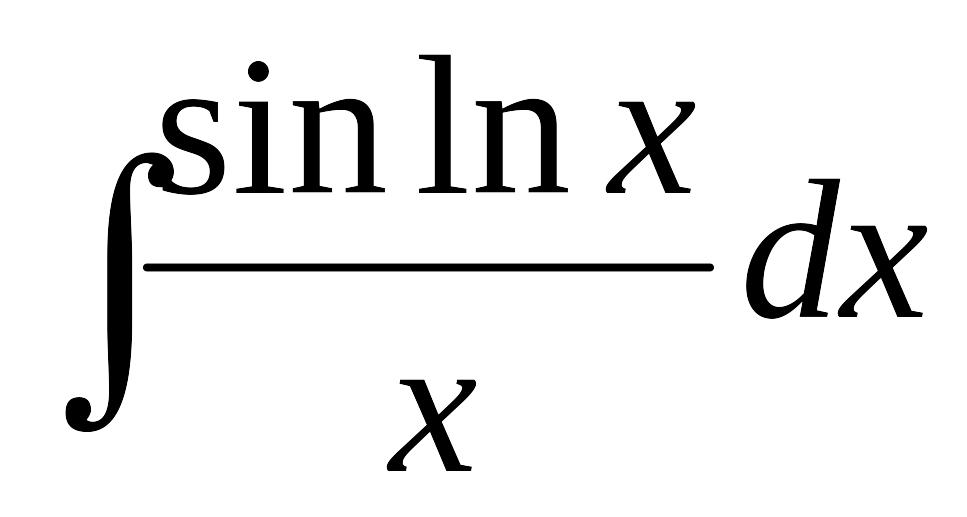
А)
![]() В)
В)![]() С)
С)
![]()
Д)
![]() Е)
Е)
![]()
Найти интеграл:
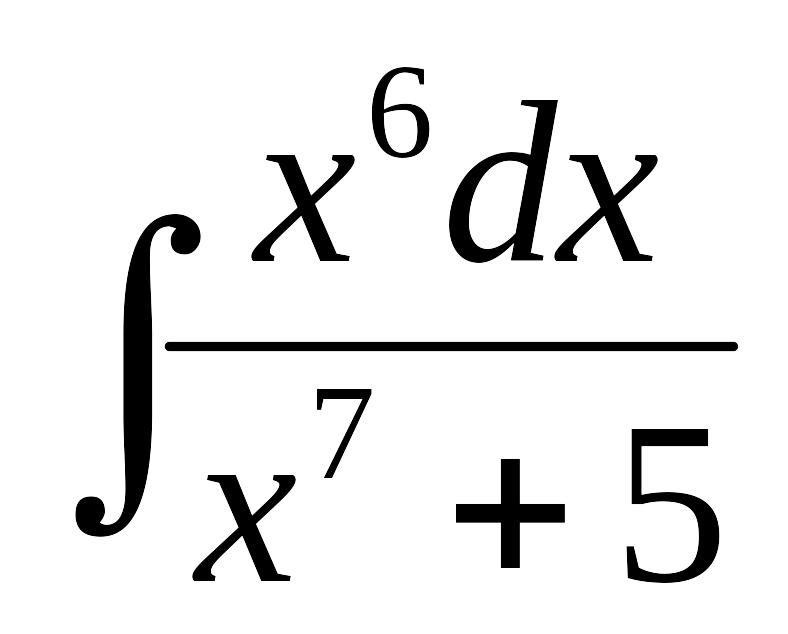 .
.
А)
![]() В)
В)![]() С)
С)
![]()
Д)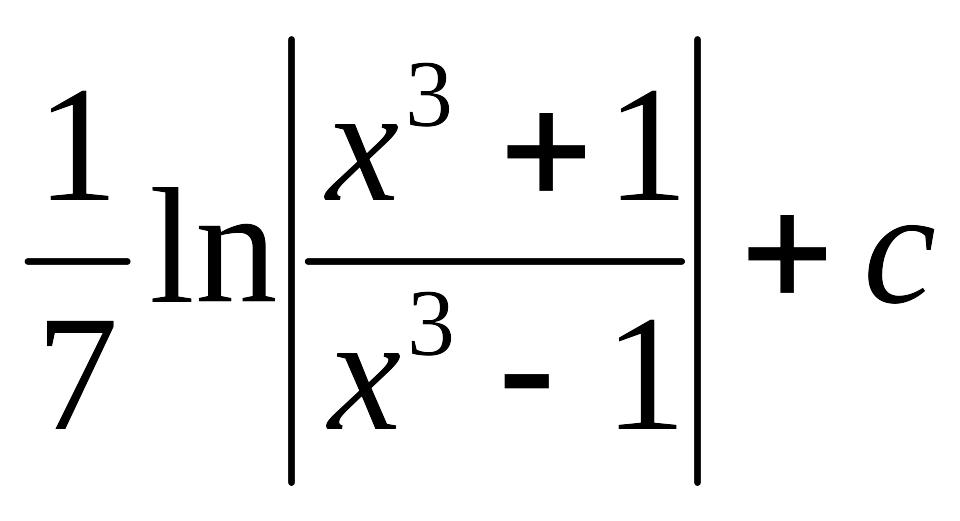 Е)
Е)
![]()
Найти интеграл:
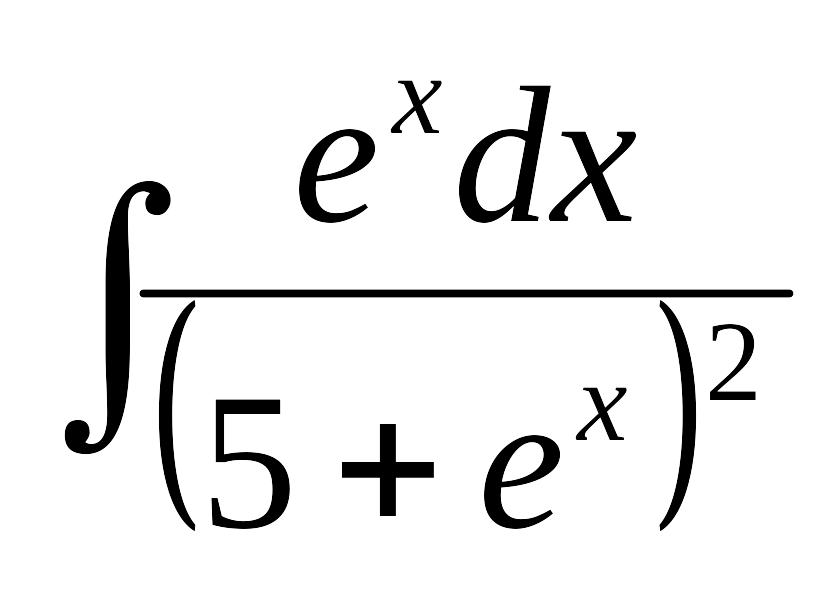
А)![]() В)
В)
![]() С)
С)
![]()
Д)
![]() Е)
Е)
![]()
Найти коэффициент при полученном выражении, после раскрытия интеграла
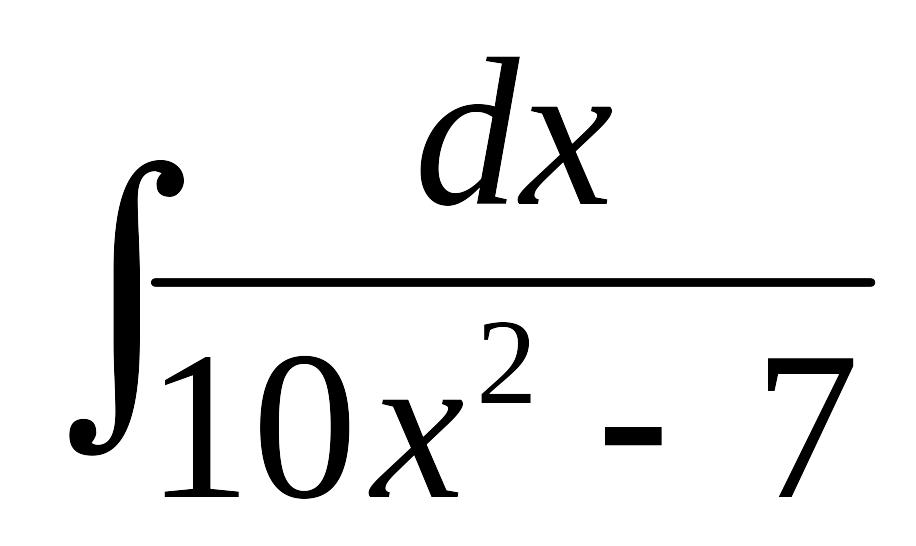
А)
![]() В)
В)
![]() С)
С)
![]() Д)
Д)
![]() Е)
Е)
![]()
