
- •I Элементы линейной алгебры.
- •Матрицы и определители. Векторная алгебра (а).
- •Аналитическая геометрия. (a)
- •3. Введение математического анализа. Функция. Предел и непрерывность (а) (b).
- •4. Производная функции одной переменной и ее приложения (а) (в).
- •Комплексные числа и операции над ними. (а) (в).
- •7. Определенный интеграл и несобственные интегралы. (а) (в).
- •Какие из этих формул написаны правильно?
- •Какие из этих формул написаны правильно?
4. Производная функции одной переменной и ее приложения (а) (в).
 (
-
угол наклона
касательной к кривой)
характеризует:
(
-
угол наклона
касательной к кривой)
характеризует:
1. Дифференциал функции в точке , 2. Геометрический смысл производного, 3.Механический смысл производного, 4. В точке функция имеет непрерывную производную, 5. Монотонность функции .
A.1, B.2, C.3, D.4, E. 5
Какая функция имеет производную
 .
.
1. Показательная функция, 2. Логарифмическая функция, 3. Степенная сложная функция, 4. Степенная функция, 5.Неявная функция.
A.1, B.2, C.3, D.4, E.5
Какая функция имеет производную
 .
.
1.![]() ,
2.
,
2.![]() ,
3.
,
3.
![]() ,
4.
,
4.![]() ,
5.
,
5.![]()
A.1, B.2, C.3, D.4, E.5
Формула
 характеризует:
характеризует:
1. Произодную степенной функции, 2. Производную степенной сложной функции , 3.Производную неявной функции, 4. Производную произведения,
5. Производную показательную функции.
A.1, B.2, C.3, D.4, E.5
 характеризует:
характеризует:
1. Производную
функции
,
2. Дифференциал
функции
![]() ,
,
3.Дифференциал
отношения![]() ,
4. Непрерывность функции
,
,
4. Непрерывность функции
,
5. Разрывность функции .
A.1, B.2, C.3, D.4, E.5
Выражение
 характеризует:
характеризует:
1.
Дифференциал функции
![]() ,
2.
Дифференциал функции
,
2.
Дифференциал функции
![]() ,
,
3.
Дифференциал
функции
![]() ,
4.
Дифференциал функции
,
4.
Дифференциал функции
![]() ,
,
5.
Дифференциал функции
![]() .
.
A.1, B.2, C.3, D.3, E.4
Выражение
 характеризует:
характеризует:
1.
Дифференциал
функции
![]() ,
2. Дифференциал
функции
,
2. Дифференциал
функции
![]() ,
,
3.
Дифференциал
функции
![]() ,
4. Дифференциал
функции
,
4. Дифференциал
функции
![]() ,
,
5. Дифференциал функции .
A.1, B.2, C.3, D.4, E.5
Функция

Характеризует:
1. Формулу Эйлера , 2. Формулу Лагранжа, 3. Формулу Тейлора,
4. Формулу Маклерона, 5. Теорему Коши.
A.1, B.2, C.3, D.4, E.5
Покажите достаточное условие существование экстремума функции в точке .
1.![]() ,
2.
,
2.
![]() ,
3.
,
3.
![]() ,
4.
,
4.
![]() ,
5
,
5![]()
A)1, B)2, C)3, D)4, E) 5.
Функция
 характеризует:
характеризует:
1. Формулу Эйлера , 2. Формулу Лагранжа, 3. Формулу Тейлора,
4. Формулу Маклорена, 5. Теорему Коши.
A.1, B.2, C.3, D.4, E.5
 называется:
называется:
A)
приращением
функции
![]() ;
B) дифференциалом
функции
;
;
B) дифференциалом
функции
;
C)
производной
от функции
в точке
![]() ;
;
D) приращение аргумента; E)непрерывность функции в точке .
Производная функции геометрически представляет собой:
A)площадь фигуры; B)касательной к поверхности;
C)угловой коэффициент касательной к графику функции в точке ;
D)угол наклона прямой; E)длины дуги.
Теорема Лагранжа (о конечном приращение) представляется формулой:
A)
![]() ;
B)
;
B)![]() ;
;
C)
![]() D)
D)
![]() ;
E)
;
E)![]() .
.
Правило дифференцирования сложной функции является:
A)
![]() ;
B)
;
B)
![]() ;
C)
;
C)
![]() ;
;
D)
![]() ;
E)
;
E) .
.
Формула представляет:
A)теорему Лагранжа, B)Теорему Ролля, C)Теорему Коши,
D)теорему Ферма, E)правило Лопиталя.
Задачи Производная функции одной переменной и ее приложения (В).
Найти производную функции

A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]() .
.
Найти производную третьего порядка функции

A)
![]() B)
B)
![]() C)
C)![]()
D)
![]() E)
E)
![]() .
.
Найти дифференциал функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)![]()
Дана функция
 Найти
Найти

A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]()
Дана функция
 Найти
Найти
A)
![]() B)
B)
![]() C)
C)
![]() D)
1 E)
D)
1 E)
![]() .
.
Найти дифференциал функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Найти дифференциал второго порядка функции

A)
![]() B)
B)
![]() C)
C)
![]() D)
0 E)
D)
0 E)
![]() .
.
Найти производную функции
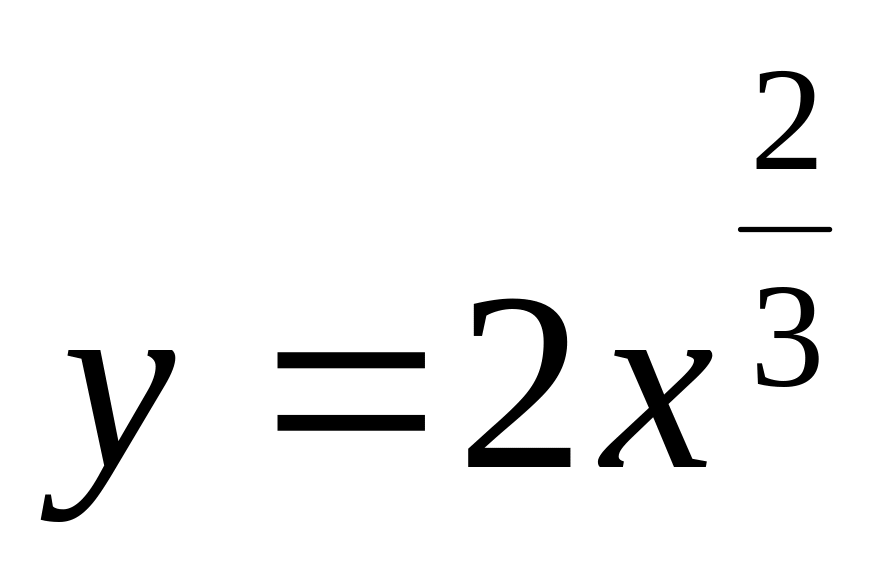
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)![]() E)
1.
E)
1.
Найти производную функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Найти производную функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Найти
A) 3 B) C) 4 D) 0 E) 1
Найти
A) 5 B) C)1 D) 0 E)
Найти производную третьего порядка функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Найти дифференциал функции

A)
![]() B)
B)![]() C)
C)![]()
D)
![]() E)
E)
![]()
Дана функция
 . Найти
. Найти
A)
![]() B)
C)
B)
C)
![]() D)
D)
![]() E)
E)
![]()
Дана функция
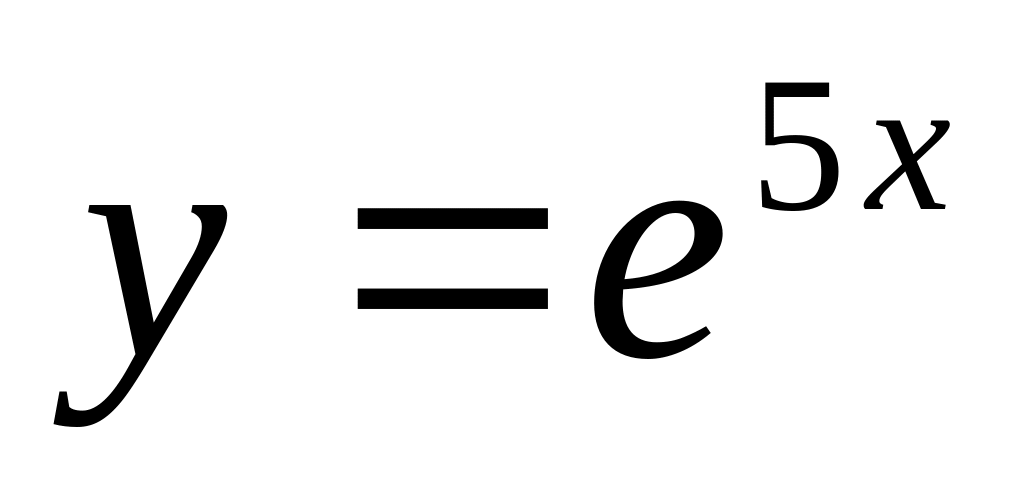 .
Найти
.
Найти
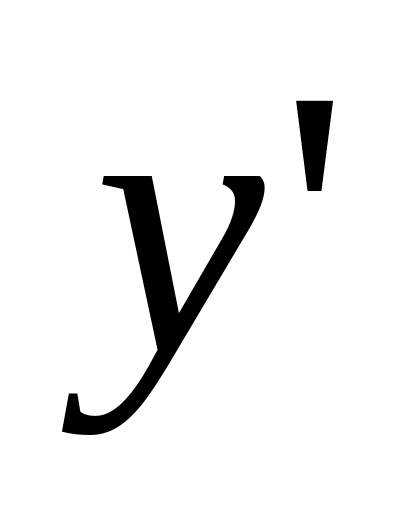 .
.
A)
![]() B)
B)
![]() C)
C)![]() D)
D)
![]() E)
E)
![]() .
.
Найти дифференциал второго порядка функции

A)
B)
![]() C)
C)
![]() D)
D)![]() E) 0.
E) 0.
Найти дифференциал функции

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Найти дифференциал второго порядка функции
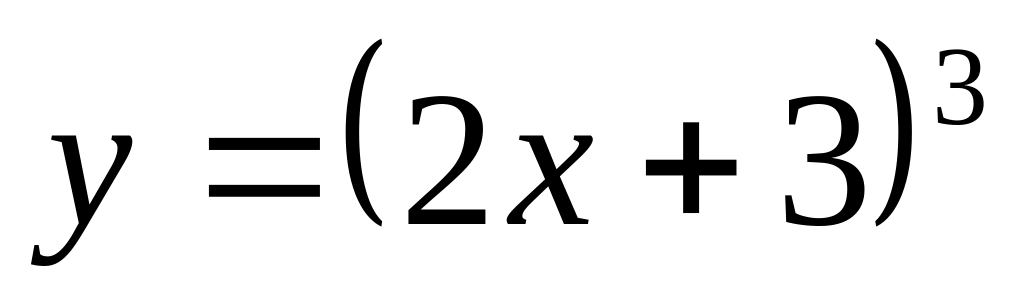
A)
![]() B)
B)
![]() C)
C)
![]() D) 0
E)
D) 0
E)
![]()
Найти предел

A)
1
B)
0 C)
D)
![]() E)
E)
Найти производную функции
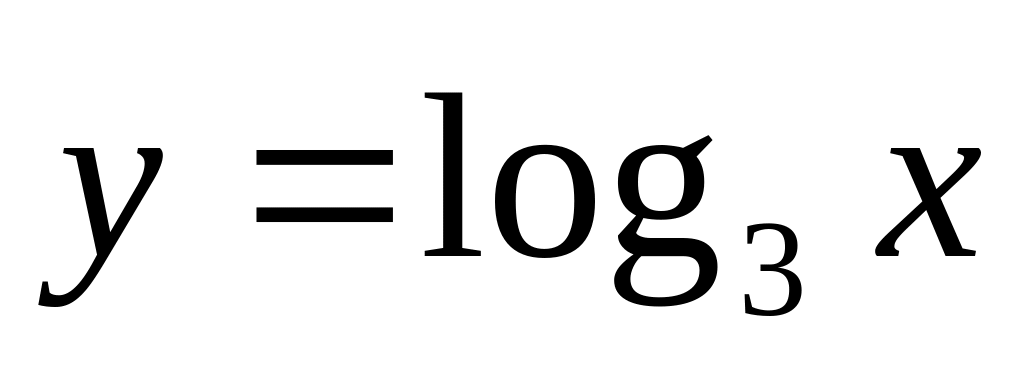 .
.
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]()
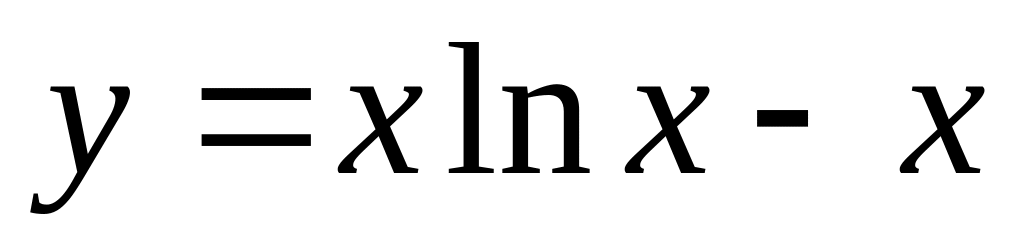 Найти
Найти
 .
.
A) -1 , B) -2, C) 0 , D) , E)
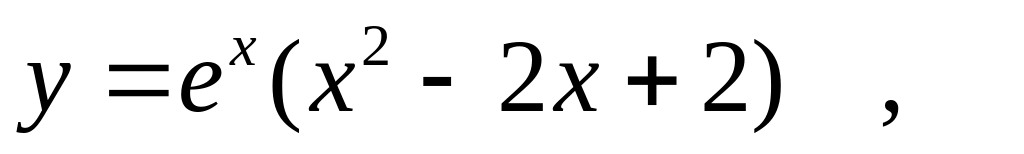 Найти
Найти
A)
,
B)
![]() ,C)
,C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
![]()
 =
?
=
?
A) 0, B) 1, C) , D) -2, E) 2
Вычислить:
A)3, B)3, C)5, D) , E) 1
Вычислить
A) , B) 1, C) , D) -2, E) 30
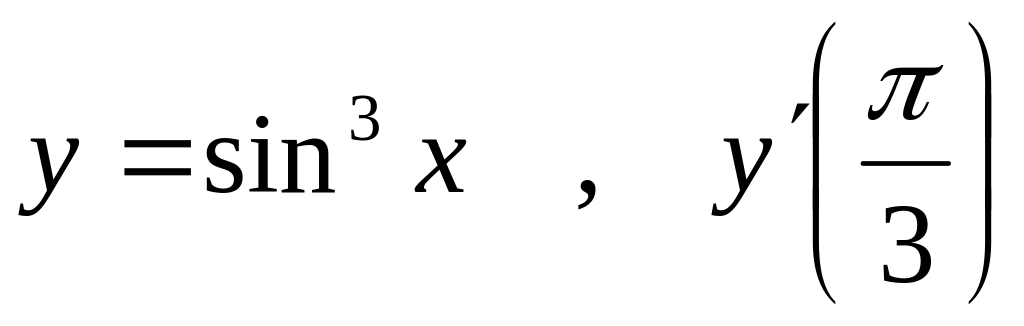 =?.
=?.
A)
,
B)
![]() ,
C)
,
C)
![]() ,
D)
,
D)
![]() ,E)
,E)
 Найти
Найти .
.
A) 0, B) , C) 1 , D) -2, E) -1
Найти производную функции :
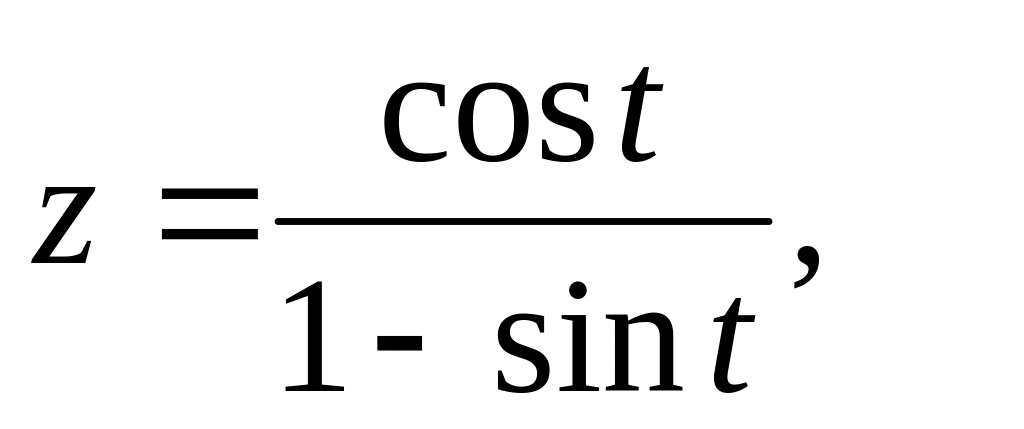 в
точке
в
точке

A)2, B)-1, C)0, D) 15, E) 1
Найти производную функции:
 .
.
A)
![]() ,
B)
,
B)
![]() , C)
, C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
![]()
Найти дифференциал 2-го порядка функции
 .
.
A)
![]() , B)
, B)
![]() ,
C)
,
C)
![]() ,
,
D)
![]() , E)
, E)
![]()
Найти производную неявной функции
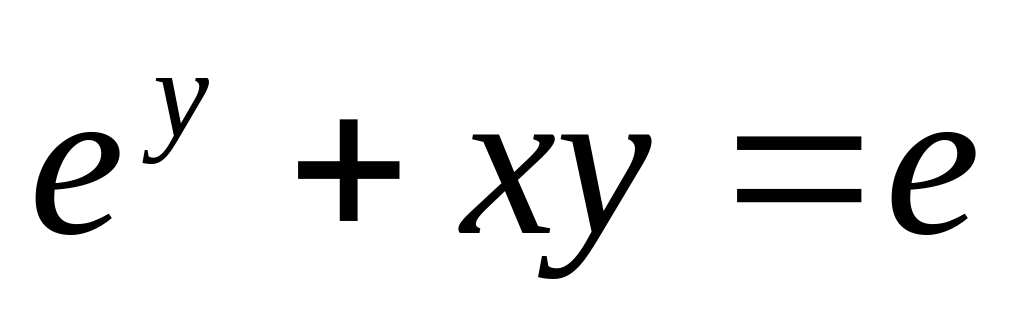 ,
,
 в точке (0,1).
в точке (0,1).
A)
![]() , B)
, B)
![]() ,
C)
,
D)
,
C)
,
D)
![]() , E)
, E)
![]()
Найти производную функции:

A)
![]() , B)
, B)
![]() , C)
, C)
![]() , D)
, D)
![]() ,E)
,E)
![]()
Найти производную функции:

A)
![]() , B)
, B)
![]() ,
C)
,
D)
,
C)
,
D)
![]() , E)
, E)
![]() .
.
Найти производную 5-го порядка функции
 .
.
A)![]() ,
B)
,
B)
![]() , C)
, C)![]() , D)
, D)
![]() ,
E)
,
E)
![]()
Вычислить производную функции
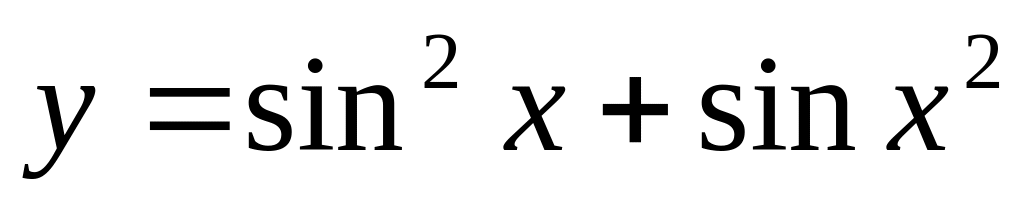 в
точке
в
точке
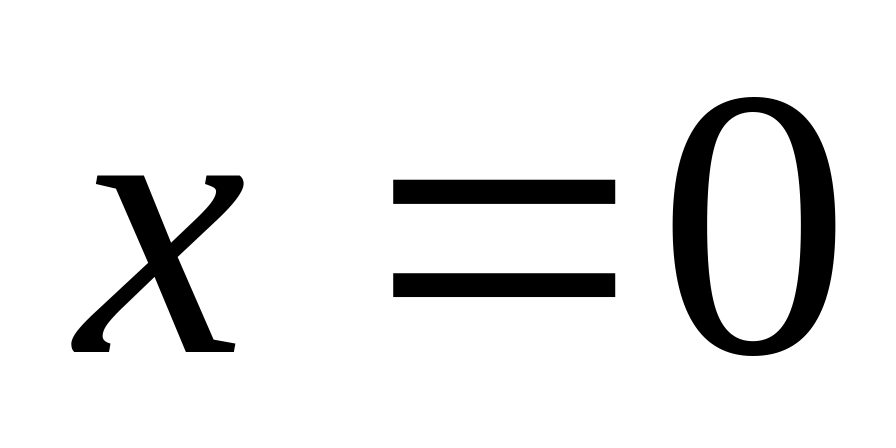 .
.
A) 1, B) , C) 5 , D) , E) 0
Найти дифференциал функции
 :
:
A)
![]() , B)
, B)
![]() , C)
, C)
![]() ,
,
D)
![]() , E)
, E)
![]()
С помощью правила Лопиталя вычислить предел:
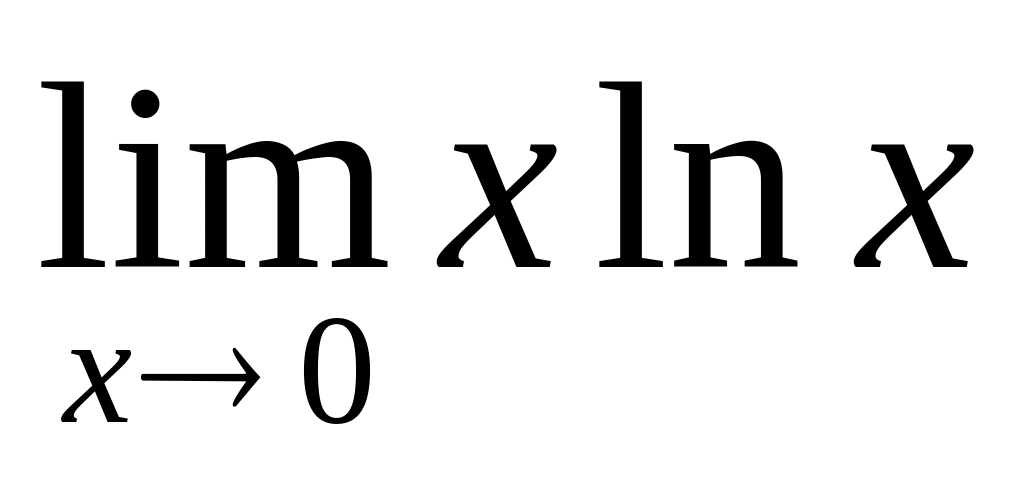
A) 0 , B) 1 , C) , D) 2, E)
С помощью правила Лопиталя вычислить предел::
 .
.
A) 2, B)3, C)0, D)1, E) -1
С помощью правила Лопиталя вычислить предел:
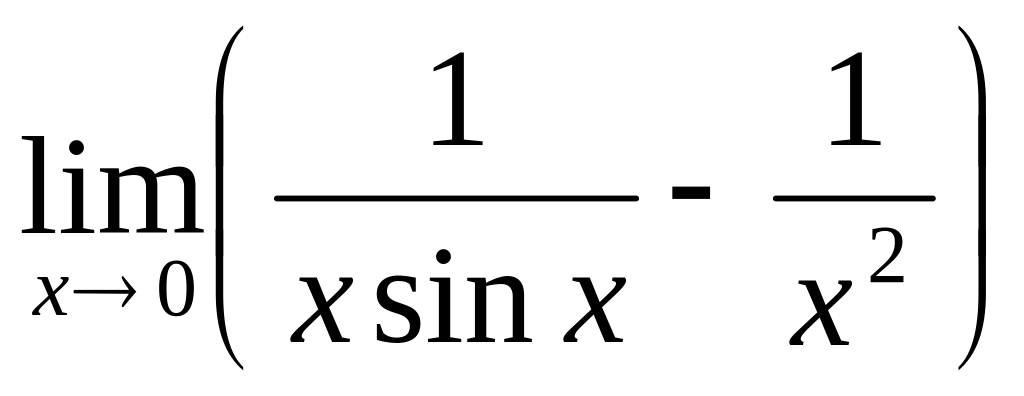 .
.
A) , B) , C) 0 , D)1, E) -1
С помощью правила Лопиталя вычислить предел:
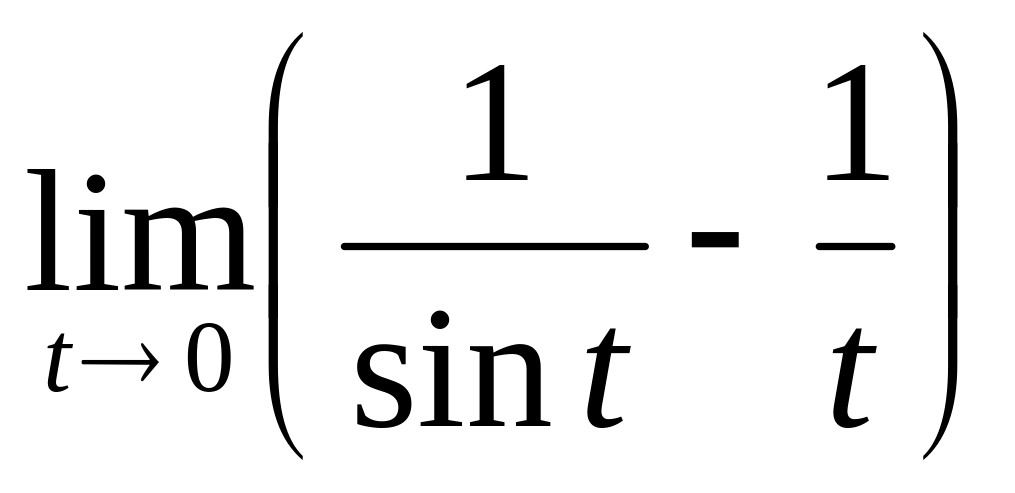 .
.
A) 1, B) -1, C)2, D) 0, E)
С помощью правила Лопиталя вычислить предел:
 .
.
A) 1 ,B) -2, C) 3, D) 0, E) 2
С помощью правила Лопиталя вычислить предел:
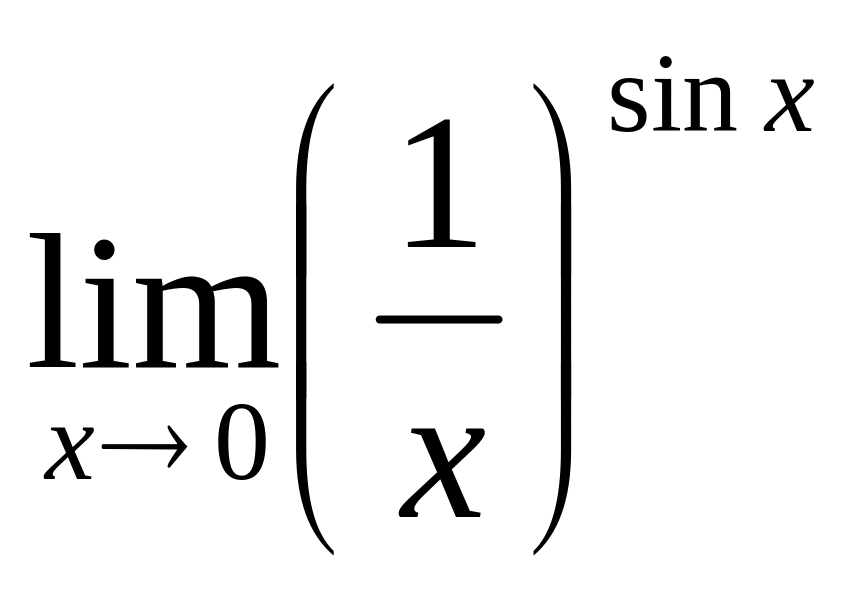 .
.
A) 0 , B) , C) 2 , D) -1 , E) 1
С помощью правила Лопиталя вычислить предел:
 .
.
A) , B) , C) 1 , D) , E) 0
С помощью правила Лопиталя вычислить предел:
 .
.
A)
,
B)
![]() ,
C)
,
C)
![]() , D)
, D)
![]() ,
E)
,
E)
![]()
