3. Введение математического анализа. Функция. Предел и непрерывность (а) (b).
Если график функции f(x) будет симметрично относительно оси ординат, что можно сказать об этой функции.
1. f(x) нечетная функция,
2. f(x) периодичная функция,
3. f(x) четная функция,
4. f(x) непрерывная функция,
5. область определения функции f(x) неизвестна
A. 1, B.2, C.3, D.4, E. 5
Как называется функция,
симметричная относительно начало координат.
1. f(x) - нечетная функция, 2. f(x) непериодическая функция ,
3. f(x)
функция с
периодом
,
4. f(x) - четная функция,
5. f(x) - непрерывная.
A.1, B.2, C.3, D4, E.5
Равенство
характеризует:
1. функция
имеет придел
в точке
,
2. функция в точке имеет правый предел,
3. функция в точке имеет левый предел,
4. функция непрерывна в точке - ,
5. функция в точке разрывная.
A.1, B.2, C.3, D.4, E.5
характеризует:
1. Предел отношения бесконечно малых,
2. Предел отношения эквивалентных бесконечно малых ,
3. Первый замечательный предел,
4. Второй основной замечательный предел,
5. Предел тригонометрической функции.
A.1, B.2, C.3, D.4, E.5
характеризует:
1. Первый замечательный предел,
2. Второй основной замечательный предел,
3. Предел, приводящий к числу ”e”,
4. Нахождение
лимита типа
,
5. Лимит о
бесконечно малых.
A.1, B.2, C.3, D.4, E.5
характеризует:
1.Функция
имеет
в точке
имеет правый
предел,
2. Функция
имеет
в точке
имеет левый предел, 3.Функция
в точке
непрерывная,
4. Функция определена в точке , 5.Функция в точке имеет точку разрыва 1-го рода.
A.1, B.2, C.3, D.4, E.5
Если точка является точкой разрыва функции , в этой точке имеется конечный правый и левый предел этой функциии, и они равны друг другу, что можно сказать об этой функции:
1.Функция непрерывна в точке , 2. Функция непрерывна в точке слева, 3. Функция имеет в точке прыжковую точку разрыва, 4. Функция имеет в точке точку разрыва 2-го рода, 5. Функция в точке имеет устраняющуюся точку разрыва .
A.1, B.2, C.3, D.4, E.5
Если существуют конечные пределы
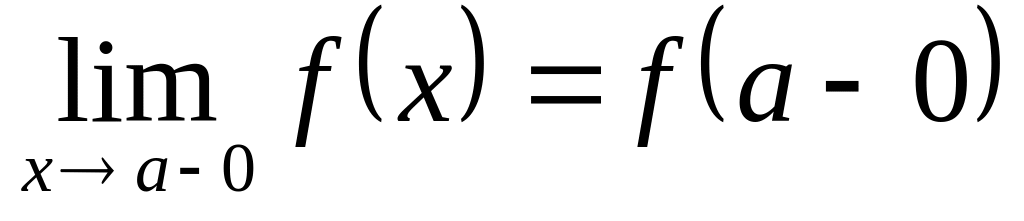и
,
,
то
называется:
A)точкой разрыва I рода, B) пределом функции ,
C) стационарной точкой, D) точкой перегиба,
E) бесконечно малой величиной.
Пусть
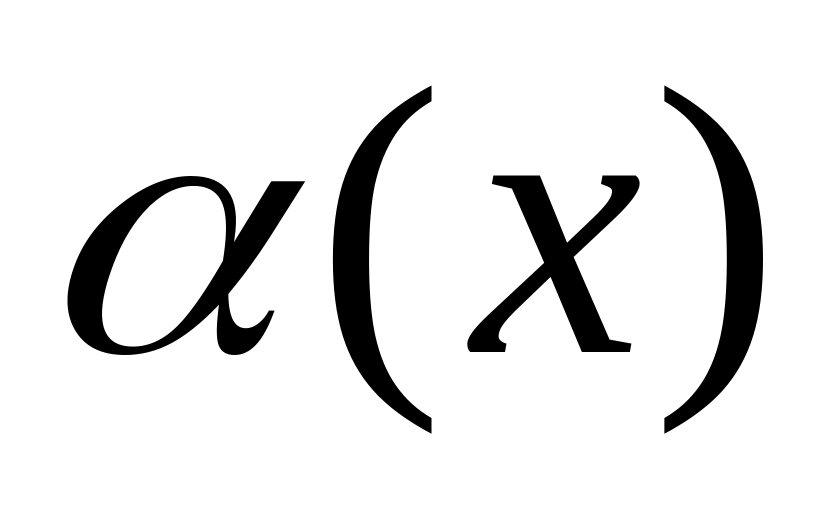и
-
бесконечно малые при
.
Если
,
то
A)
и
малые одного итого же порядка,
B) и эквивалентные бесконечно малые величины,
C) является бесконечно малой высшего порядка с ,
D) является бесконечно малой высшего порядка по сравнению с ,
E)
.
и являются эквивалентными, если
А)
В)
С)
D)
Е)
Задачи (В).
Вычислить
A) 3 B) 0 C) 2 D) -1 E)-3.
В каких точках функция
имеет разрывы?
A)
B)
C)
D)
Только в точке
E)
Только в точке
.
Найти предел
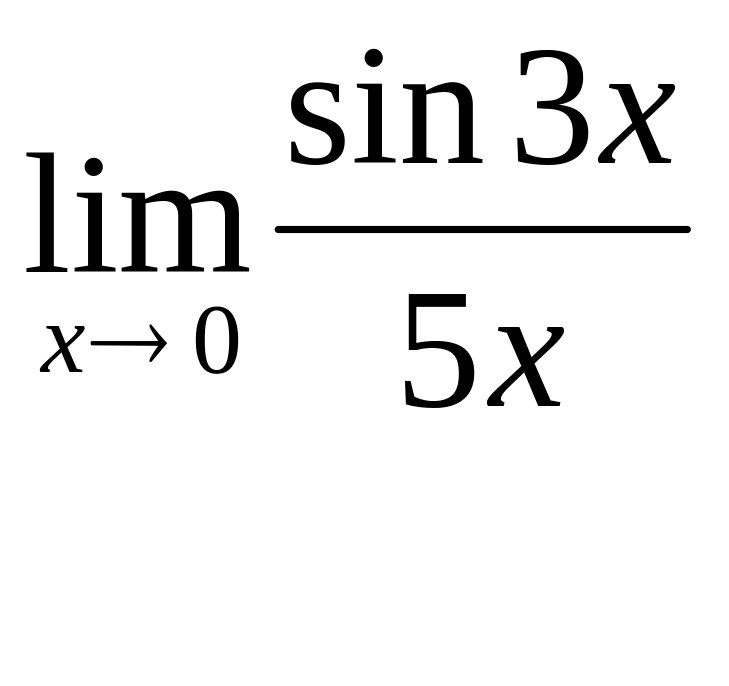
A)
B)
1
C)
D)
0
E)
.
Найти предел
A) 3 B) -2 C) 0 D) 2 E) 4.
Найти
A)
5 B)
4 C)
D)
E)
0.
Найти
A)
3 B)
C)
0 D)
1 E)
.
Найти предел
A) 1 B) 0 C) -2 D) E) 2.
Найти предел
A)1
B)0
C)
-3 D)
E)
.
Найти предел
A)
B)
1
C)
D)
0 E)
.
Вычислить
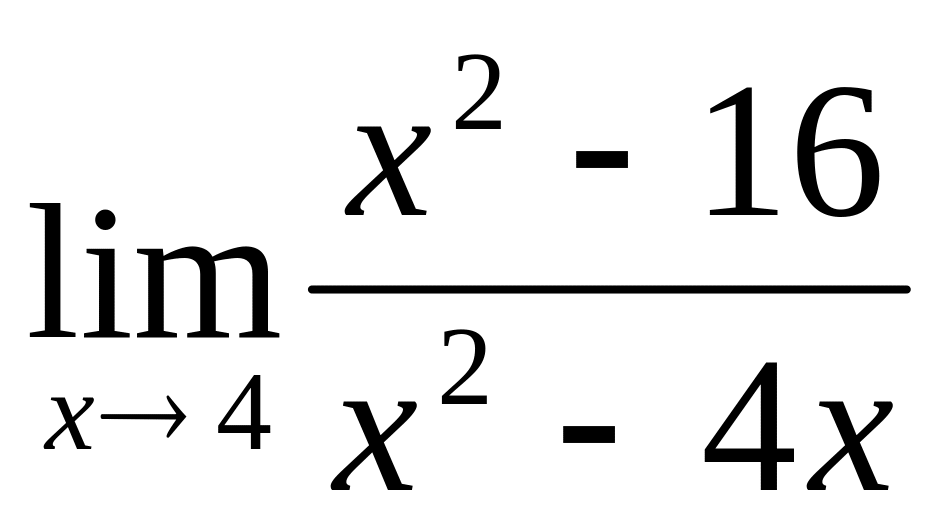
A) 3 B) 7 C) 2 D) 0 E) -3.
В каких точках функция
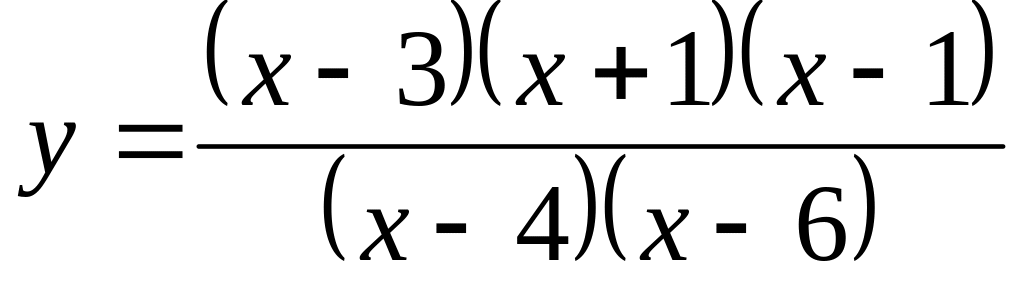имеет разрывы?
A)
B)
только в точке
C)
D)
E)
только в точке
Найти предел
A)
B)
0
C)
3
D)
E)
1.
Найти предел
A) B) 1 C) -1 D) 0 E) 5.
Найти
A)
3
B)
C)
4
D) 0
E) 1
Найти
A)
5
B)
C)1
D) 0
E)
Найти предел
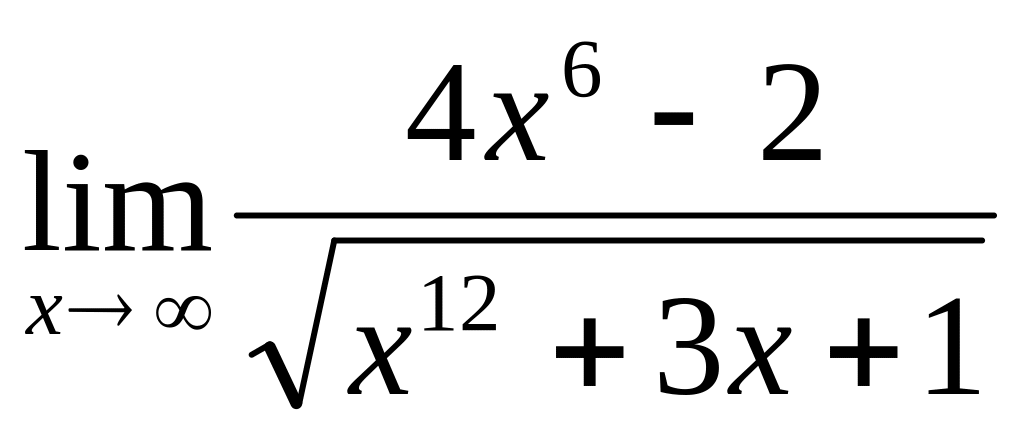
A) 1 B) C) 0 D) 12 E) 4
Найти предел
A)
B)
C)
1
D) 0
E)
.
Найти предел
A) 8 B)4 C)1 D) 0 E) 3.
Вычислить предел
A)3, B)3, C)5, D) , E) 1
Вычислить предел
A)
,
B) 1, C)
,
D) -2, E) 30
Вычислить предел
A)1, B)2, C)3, D) 0, E) 0,5
Вычислить предел
A) 5, B) , C) 1, D)0, E) 3
Вычислить предел
A)3,
B)
,
C) 1, D)
,
E)
Найти область определения функции
.
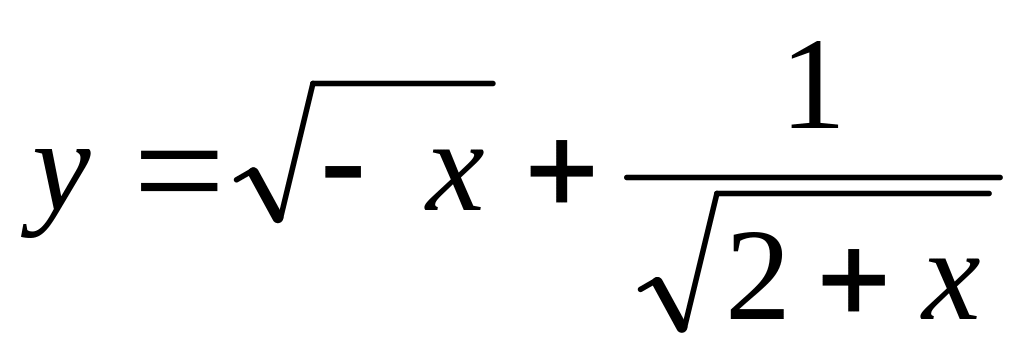A)
B)
C)
D)
E.
.
Вычислить:
A)1 ; B)2 ; C) 3; D)0 ; E)ln5