
- •I Элементы линейной алгебры.
- •Матрицы и определители. Векторная алгебра (а).
- •Аналитическая геометрия. (a)
- •3. Введение математического анализа. Функция. Предел и непрерывность (а) (b).
- •4. Производная функции одной переменной и ее приложения (а) (в).
- •Комплексные числа и операции над ними. (а) (в).
- •7. Определенный интеграл и несобственные интегралы. (а) (в).
- •Какие из этих формул написаны правильно?
- •Какие из этих формул написаны правильно?
Аналитическая геометрия. (a)
Нормальным уравнением прямой является:
А)![]() В)
В)![]() С)
С)![]()
D)![]() Е)
Е)![]()
Уравнение равнобочной гиперболы является:
А)![]() В)
В)![]() С)
С)
![]() D)
D)
![]()
Е)![]() .
.
Какое из этих уравнений не является правильным?
А)
![]() - уравнение эллипса; В)
- уравнение эллипса; В)
![]() -
уравнение гиперболы С)
-
уравнение окружности D)
-
нормальное уравнение прямой
-
уравнение гиперболы С)
-
уравнение окружности D)
-
нормальное уравнение прямой
Е)
![]() - уравнение параболы.
- уравнение параболы.
Выражение
 характеризует:
характеризует:
А) Параметрическое уравнение прямой;
В) нормальное уравнение прямой;
С) общее уравнение прямой;
D) Уравнение прямой, проходящей через две данные точки; Е) уравнение прямой "в отрезках";
Формула
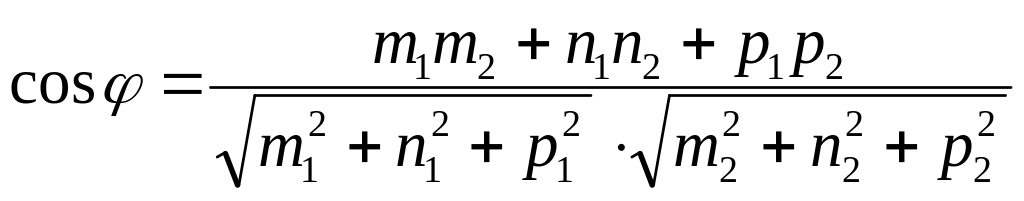 характеризует:
характеризует:
А) угол наклона; В) угол между плоскостями;
С) угол между плоскостями и прямой; D)угол поворота;
Е) угол между прямыми в пространстве.
Условия
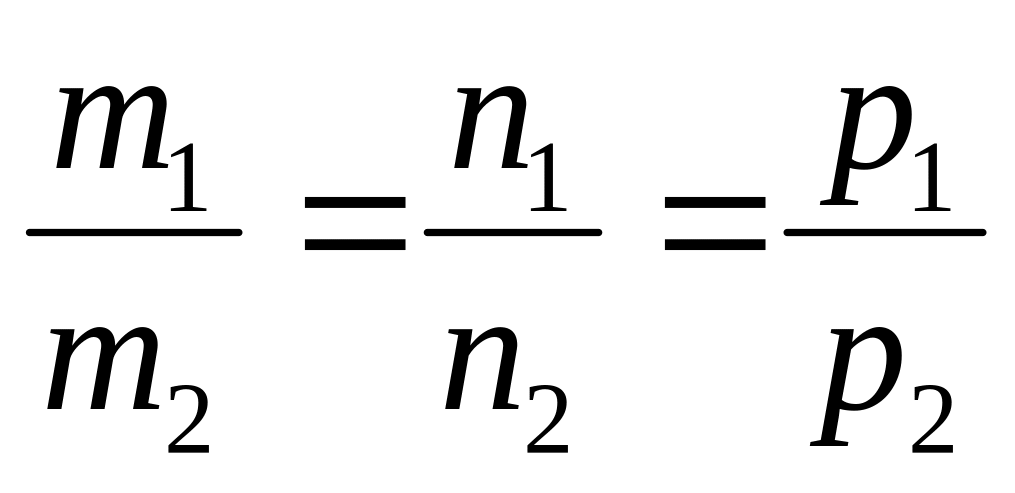 характеризует:
характеризует:
А) условию ортогональности двух векторов;
В) условию переместительности двух векторов;
С) условию параллельности двух плоскостей;
D) Условию перпендикулярности двух векторов;
Е) условию параллельности двух прямых в пространстве;
Формула
 характеризует:
характеризует:
А) угол между плоскостями; В) угол между прямыми;
С) угол между плоскостью и прямой;
D) Угол между двумя векторами; Е) угол поворота.
Какое из этих формул характеризует уравнение плоскости, проходящей через начало координат?
А)
![]() В)
В)
![]() С)
С)
![]()
D)
Е)
![]()
Система уравнений
 характеризует:
характеризует:
А) Условию параллельности двух плоскостей;
В) угол между двумя плоскостями;
С) условию ортогональности двух плоскостей;
D) Уравнению прямой в пространстве;
С) условию компланарности трех векторов.
Нормальным уравнением плоскости является:
А)
;
В)
![]() С)
С)
![]()
D)![]() Е)
Е)
![]()
Покажите нормальное уравнение плоскости
A)
![]() B)
B)![]() C)
C)
![]() D)
D)
![]() E)
E)
![]() .
.
Покажите уравнение прямой
A)
B)
![]() C)
C)![]()
D)![]() E)
E)![]() .
.
Найти уравнение прямой «в отрезках».
A)
![]() B)
B)
![]() C)
C)
D)
![]() ,
E)
,
E)
![]()
Найти каноническое уравнение эллипса.
A)
![]() , B)
, B)
![]() ,
C)
,
C)
![]() ,
D)
,
D)
![]()
E)
Аналитическая геометрия (В).
Составить каноническое уравнение гиперболы, проходящего через точки
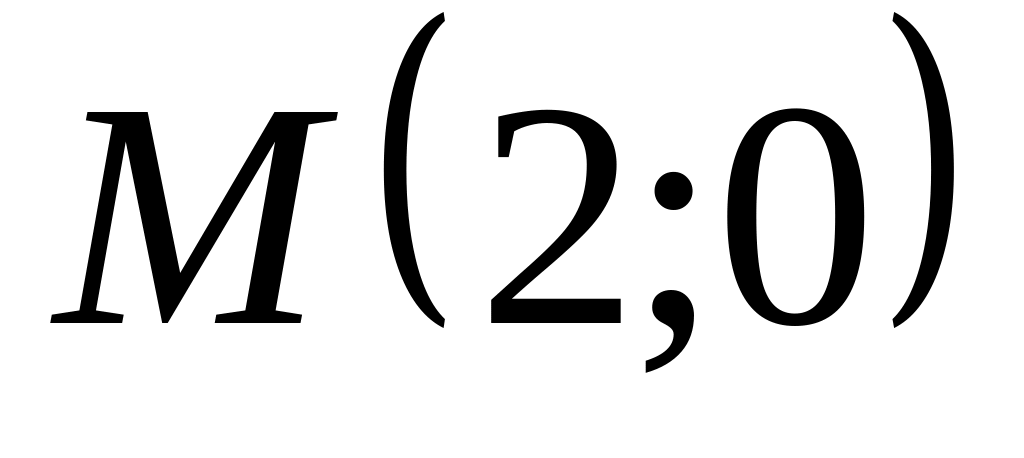 и
и
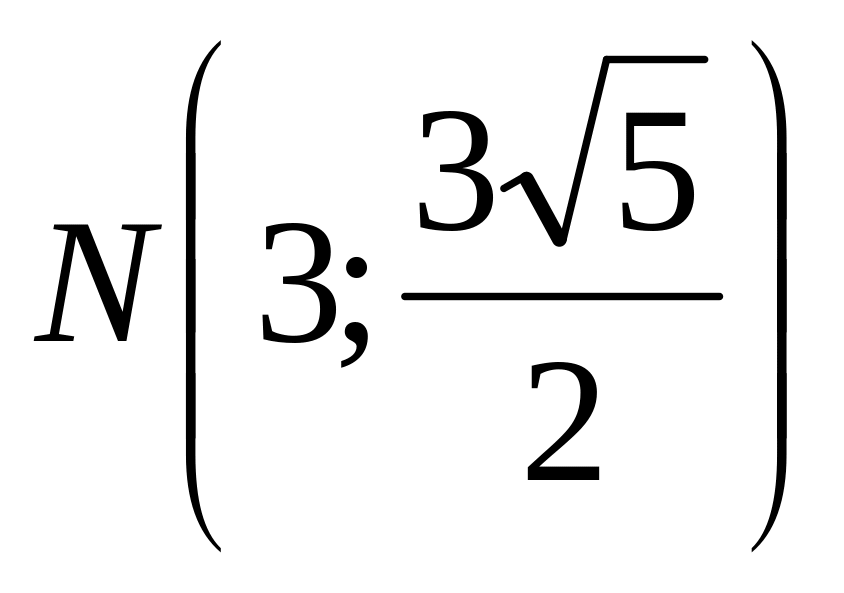
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
.
E)
.
Найти координаты центра окружности
![]()
A) (4, -3) B) (2, 11) C) (0, 0) D) (4, -2) E) (0, 3).
Найти расстояние от точки
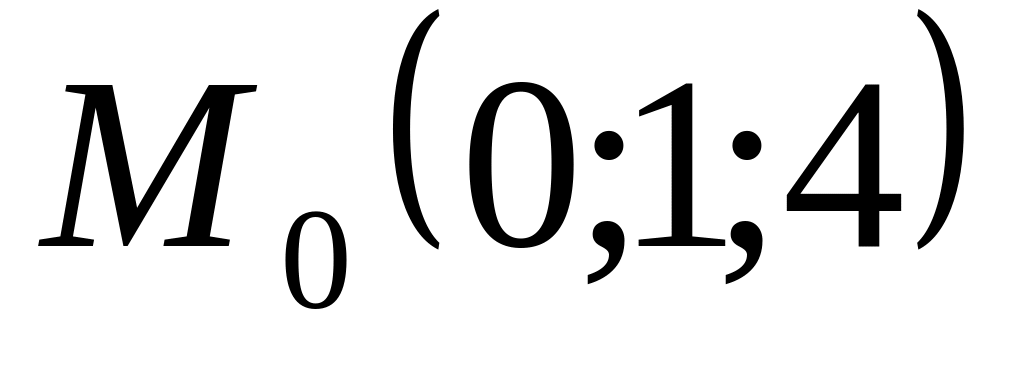 до плоскости
до плоскости
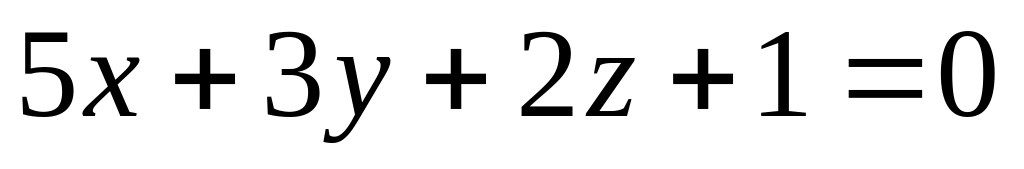
A)
![]() B)
B)
![]() C)
0 D)
C)
0 D)
![]() E)
1.
E)
1.
Найти уравнение плоскости проходящий через начало координат и через точки
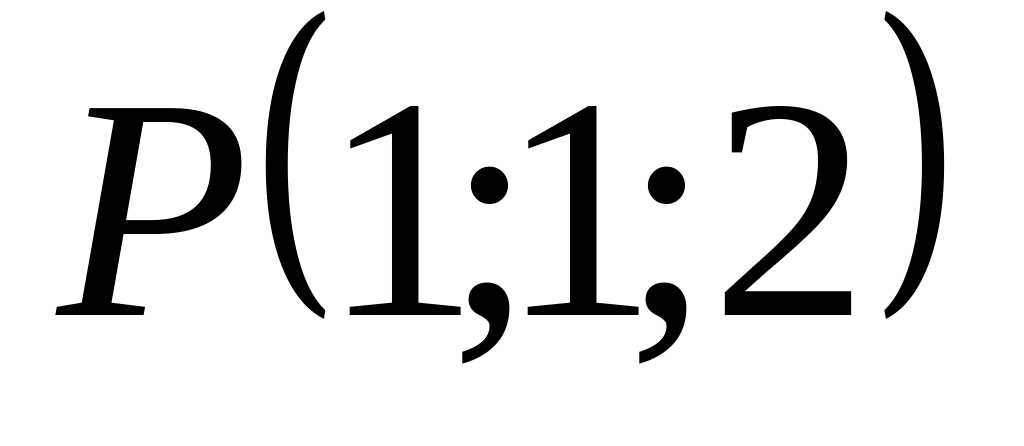 и
и
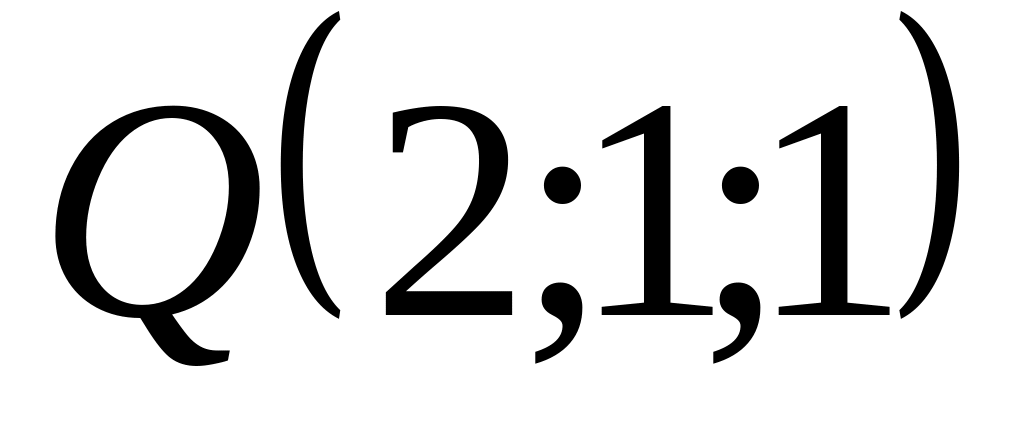
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Найти угол между прямыми
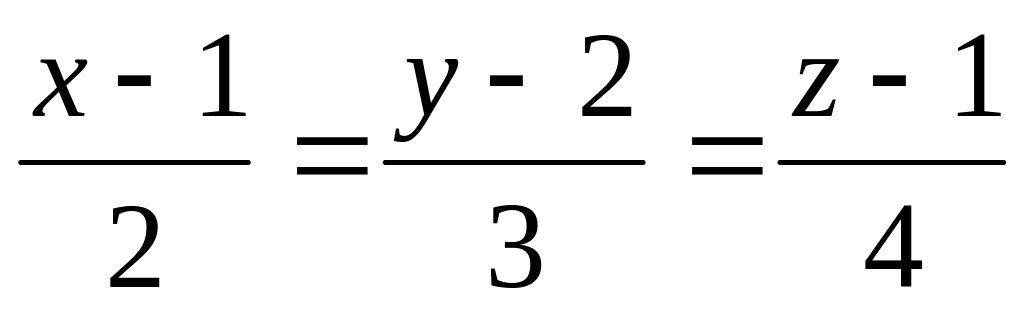 и
и
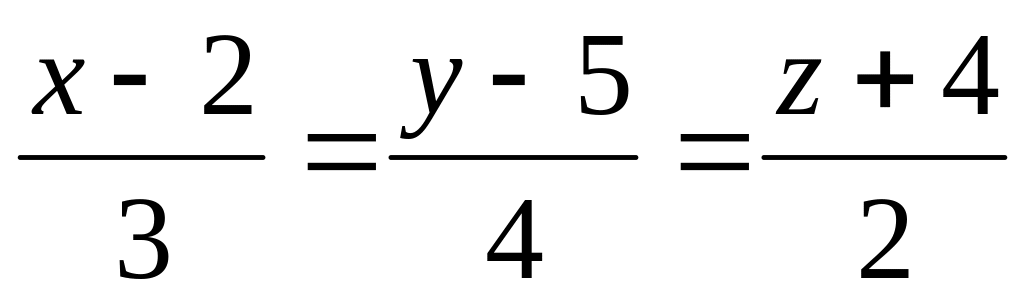
A)
![]() B)
B)
![]() C)
0 D)
C)
0 D)
![]() E)
E)
![]() .
.
Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса
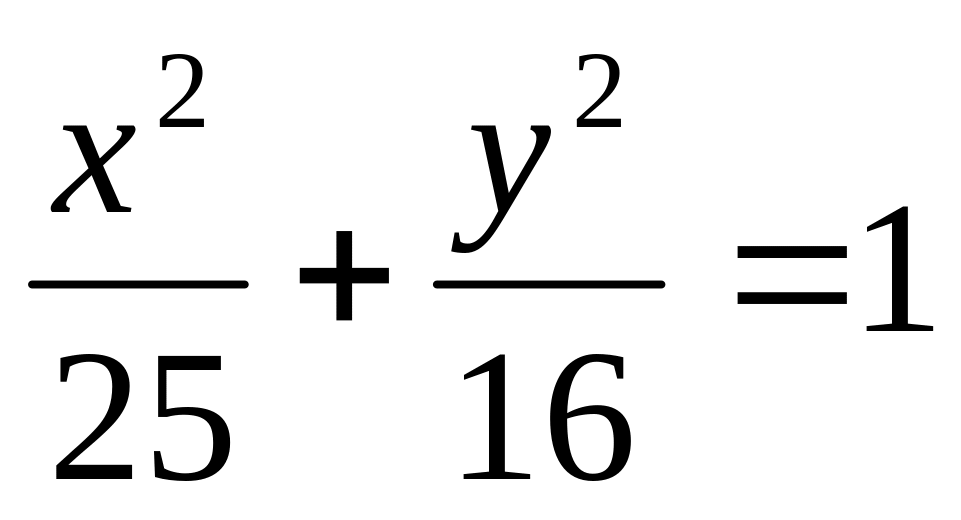
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
При каком значении
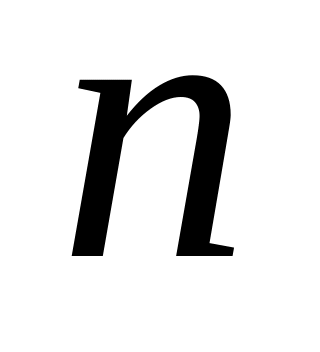 прямая
прямая
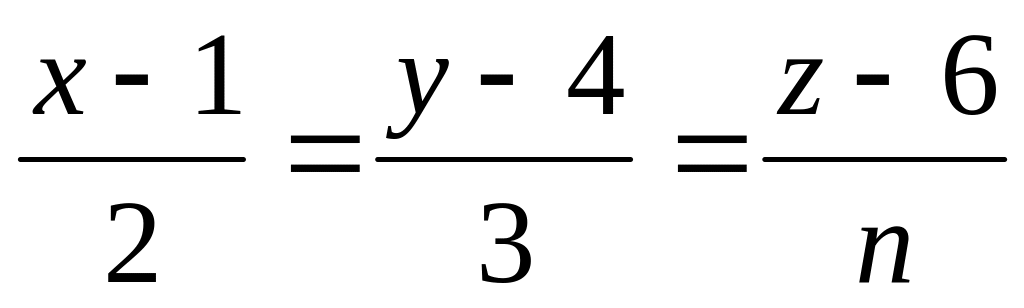 перпендикулярна плоскости
перпендикулярна плоскости
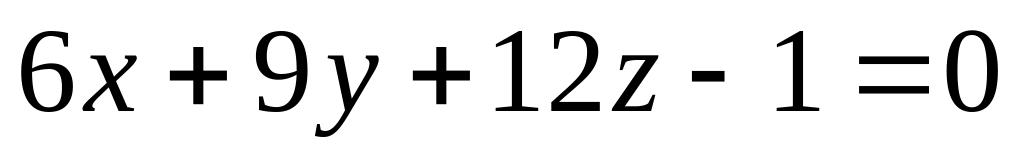
A) -1 B) 6 C) 20 D) 35 E) 4.
Найти канонические уравнения прямой, проходящей через точки
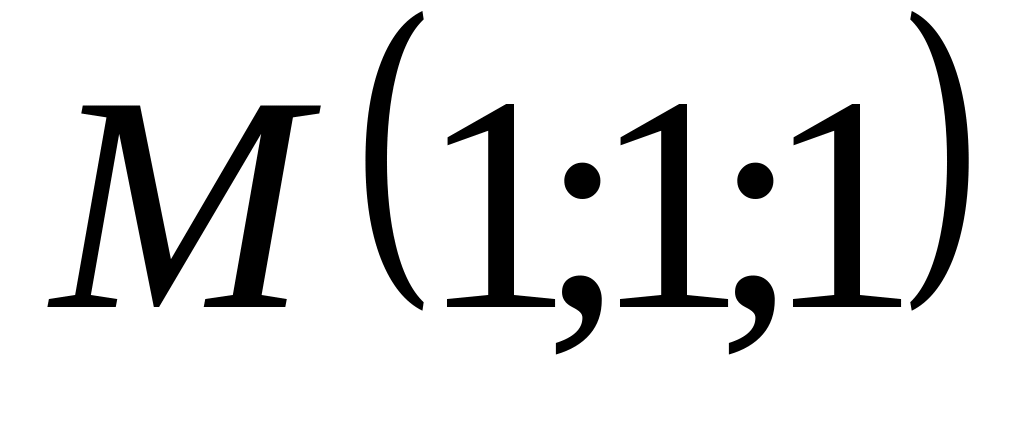 и
и
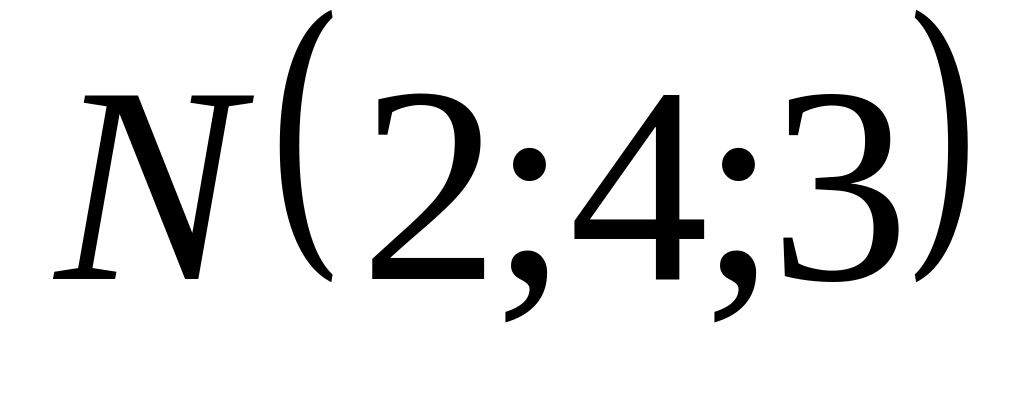
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]() .
.
Составить каноническое уравнение эллипса, проходящего через точки
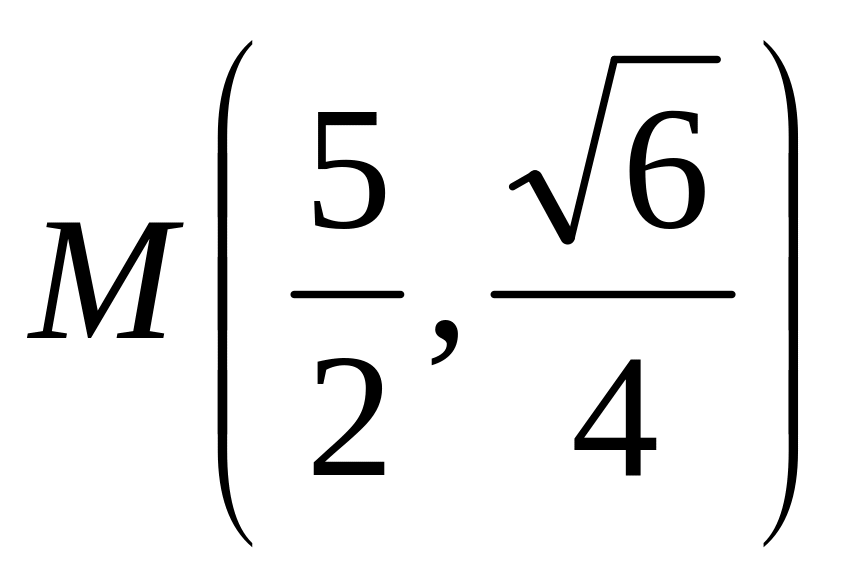 и
и
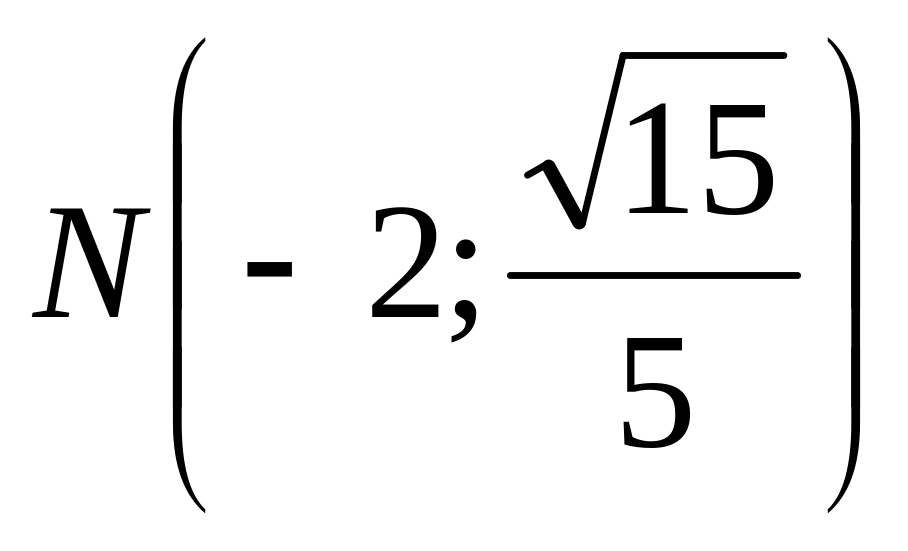
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Найти радиус окружности
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]()
Найти расстояние от точки
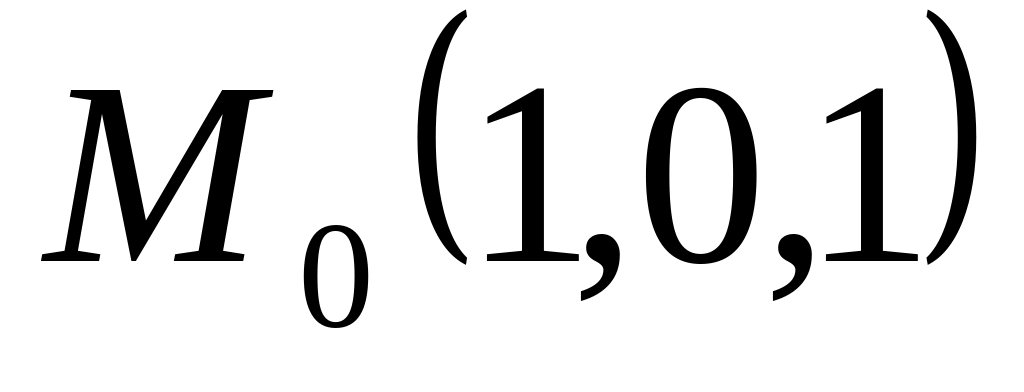 до плоскости
до плоскости
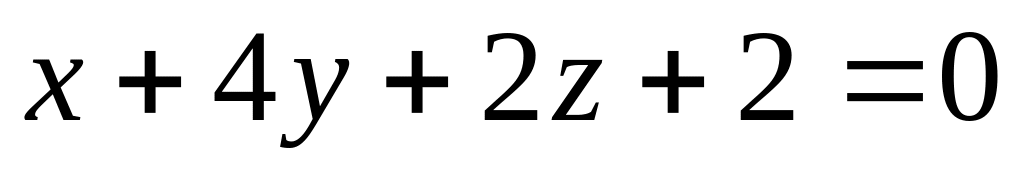
A)
![]() B)
0 C)1
D)
B)
0 C)1
D)
![]() E) 5.
E) 5.
Найти уравнение плоскости, проходящей через начало координат и через точки
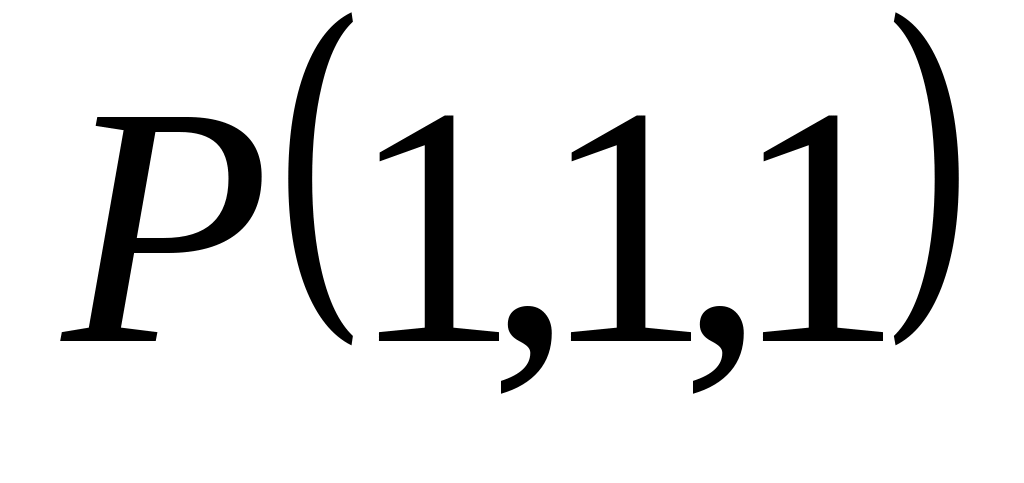 и
и
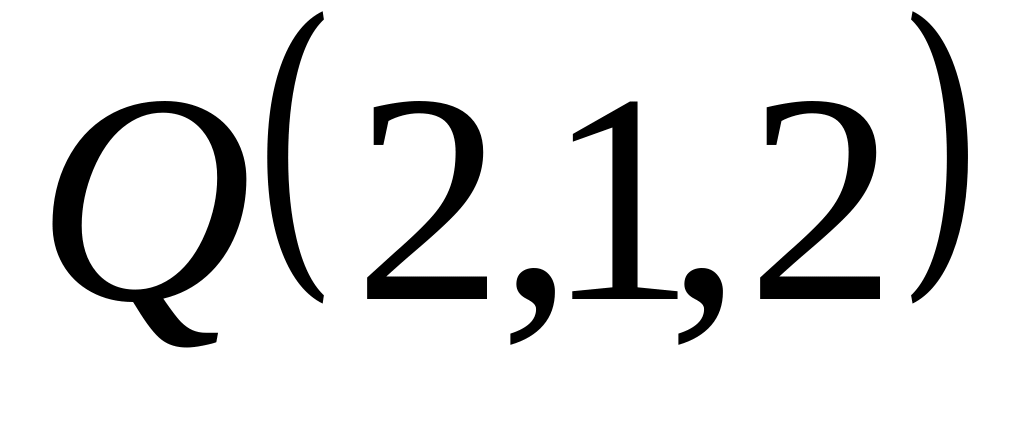
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Найти угол между прямыми
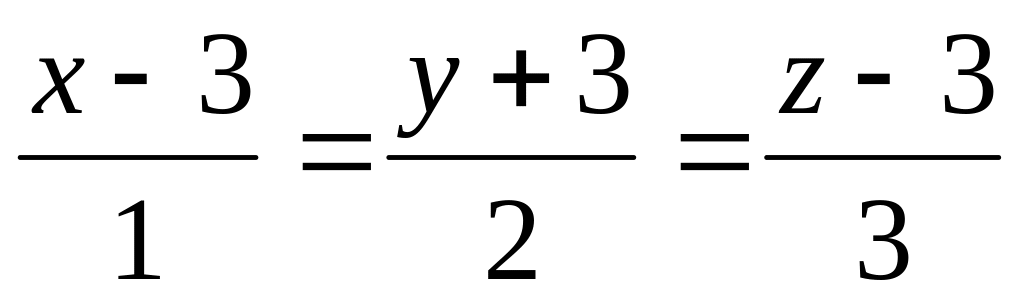 и
и
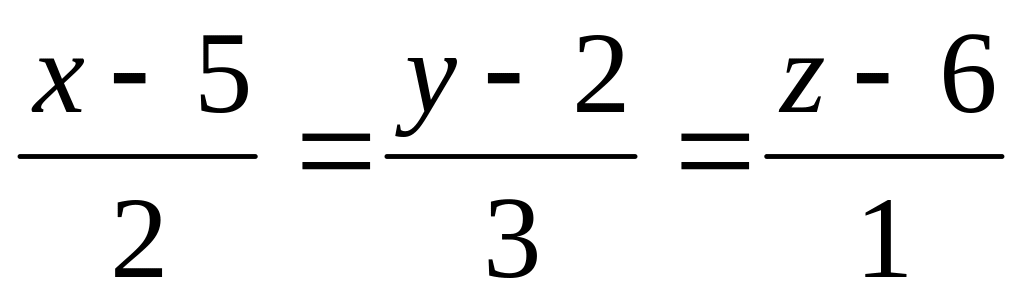
A)
![]() B)
C)
0
D)
E)
B)
C)
0
D)
E)
![]() .
.
На прямой
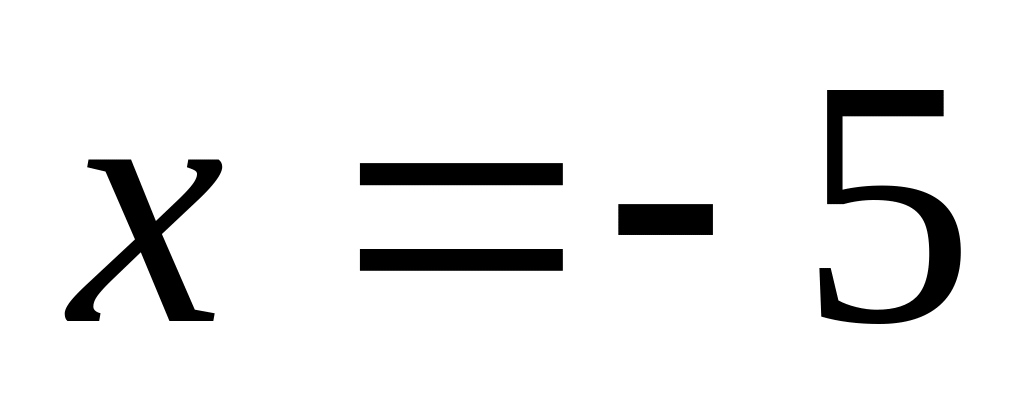 найти точку, одинаково удаленную от
левого фокуса и верхней вершины эллипса
найти точку, одинаково удаленную от
левого фокуса и верхней вершины эллипса
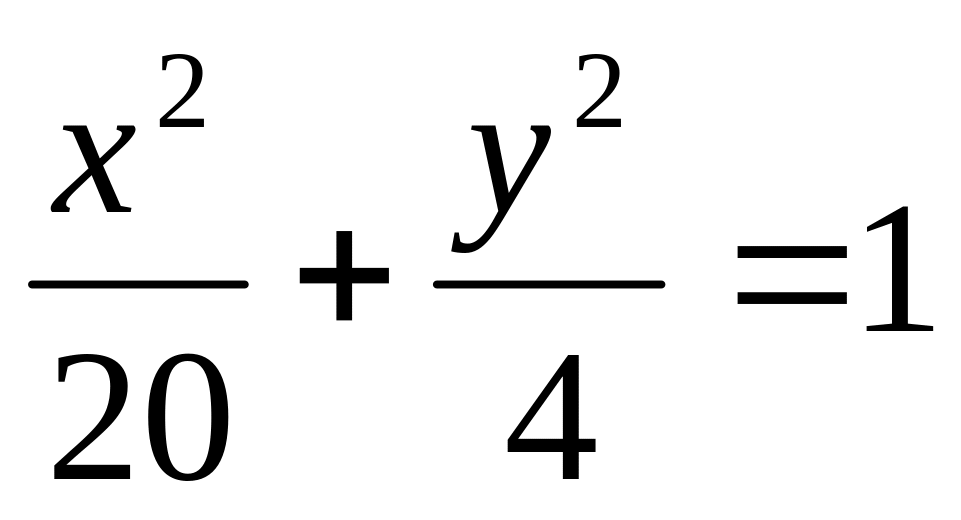
A)
![]() B)
B)
![]() C)
C)![]() D)
D)![]() E)
E)
![]()
При каком значении прямая
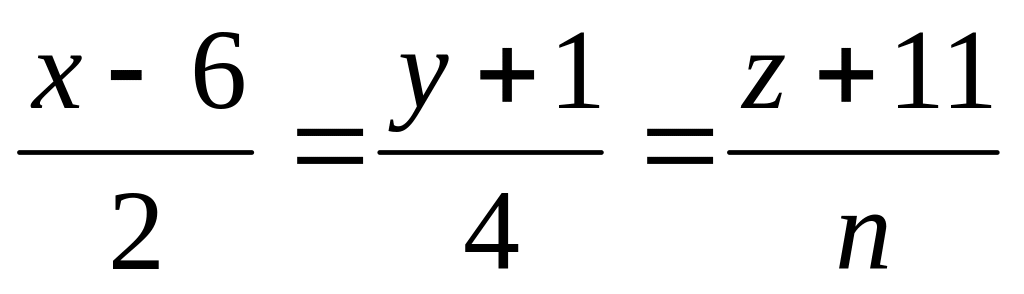 перпендикулярна плоскости
перпендикулярна плоскости
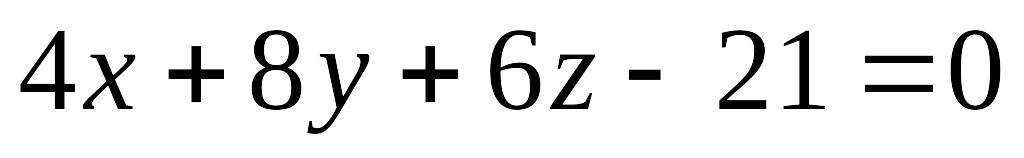 .
.
A) 1 B) 4 C) -3 D) 3 E) -1
Найти канонические уравнения прямой, проходящей через точки
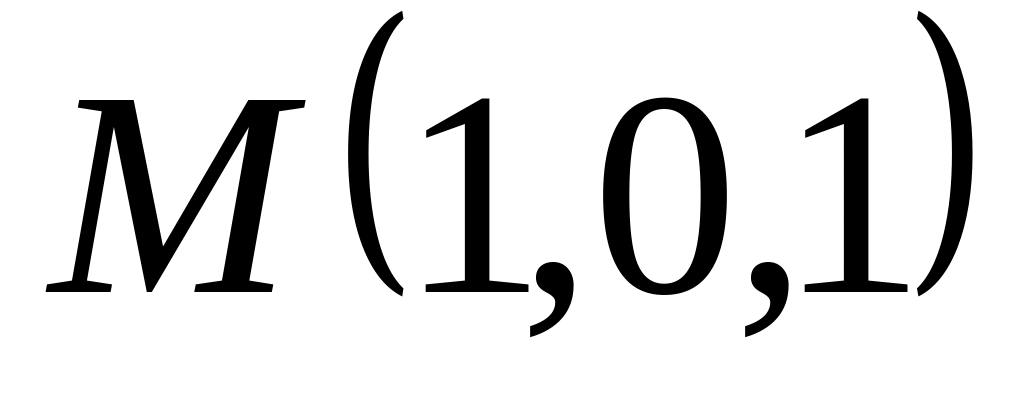 и
и
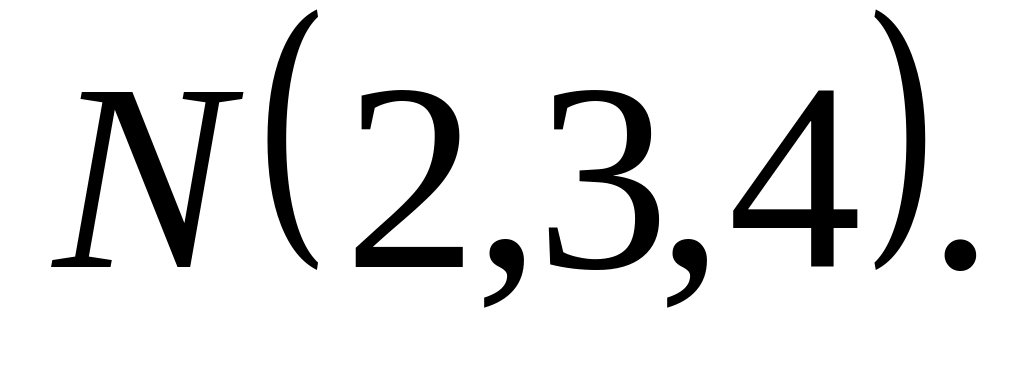
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Две стороны квадрата лежат на прямых
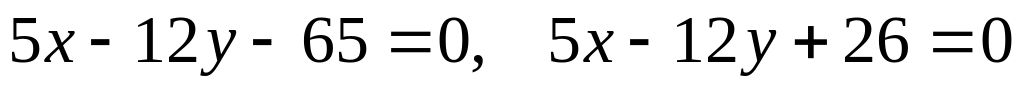 .
Вычислить его площадь.
.
Вычислить его площадь.
A) 10кв.ед. B)50кв.ед. C)49кв.ед. D)20кв.ед. E)6кв.ед.
Написать уравнение плоскости, проходящей через точку
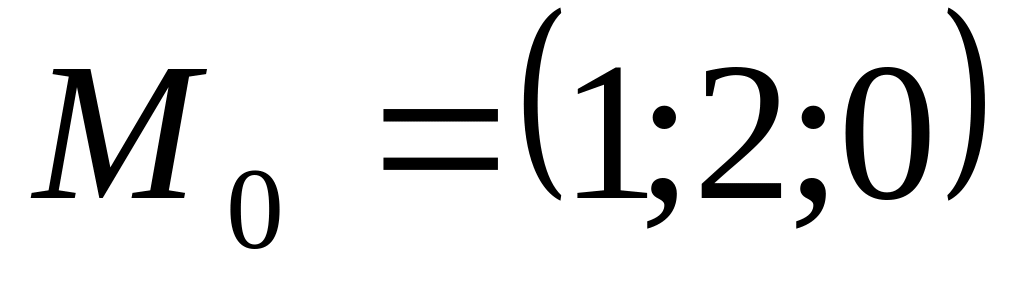
перпендикулярно к
вектору
![]()
A)
![]() B)
B)![]() C)
C)![]() D)
D)![]() E)
E)
![]() .
.
Составить уравнение прямой, проходящей через точку
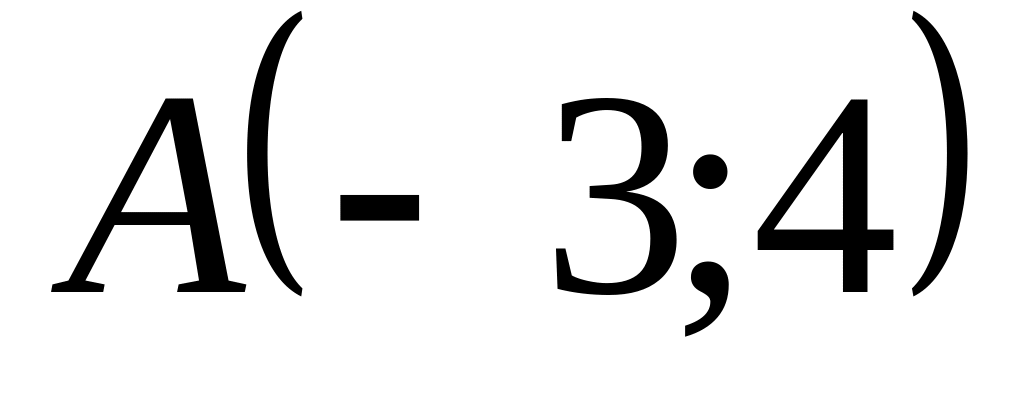 ,
перпендикулярно к прямой
,
перпендикулярно к прямой
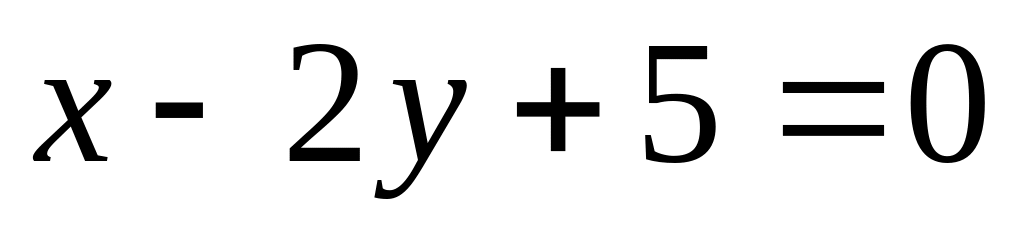
A)![]() B)
B)
![]() C)
C)![]()
D)
![]() E)
E)![]() .
.
Найти расстояние между параллельными плоскостями, заданными уравнениями
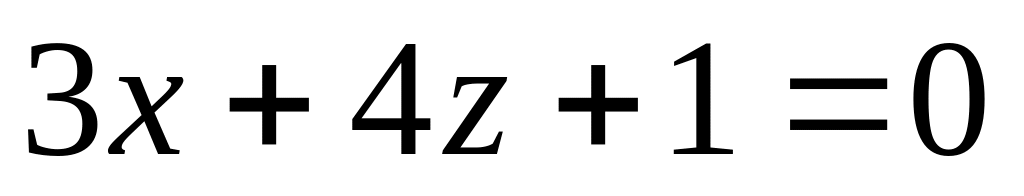 и
и
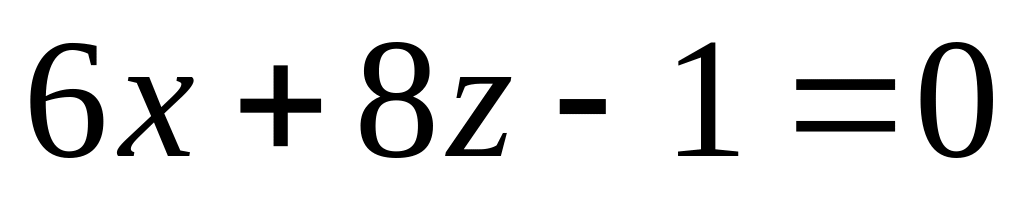
A)
![]() B)
C)
2
D)10
E)
3.
B)
C)
2
D)10
E)
3.
Найти расстояние между параллельными плоскостями, заданными уравнениями
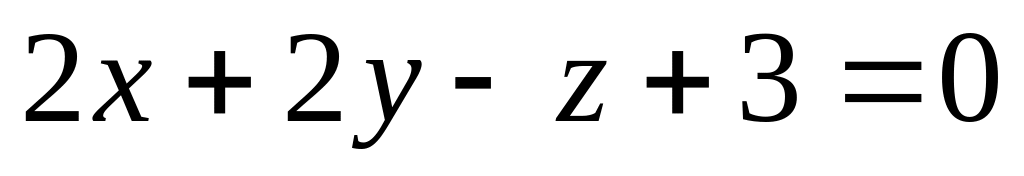 и
и
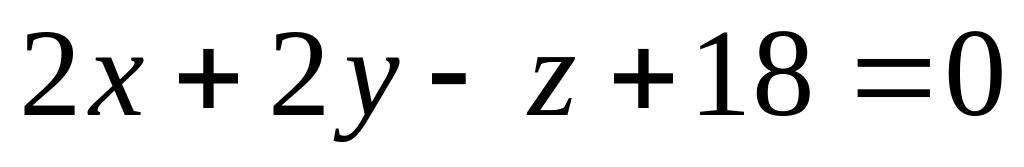
A) 6 B)3 C)2 D) 10 E) 5.
Написать уравнение плоскости, проходящей через точку
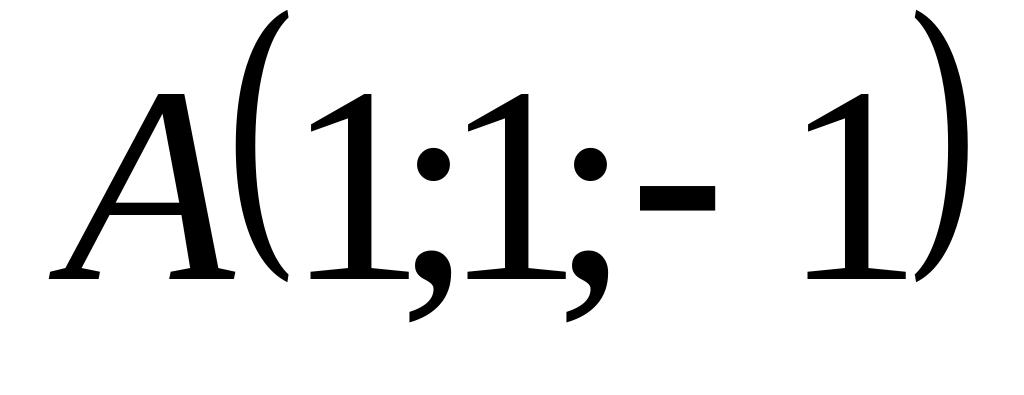 перпендикулярно к плоскостям
перпендикулярно к плоскостям
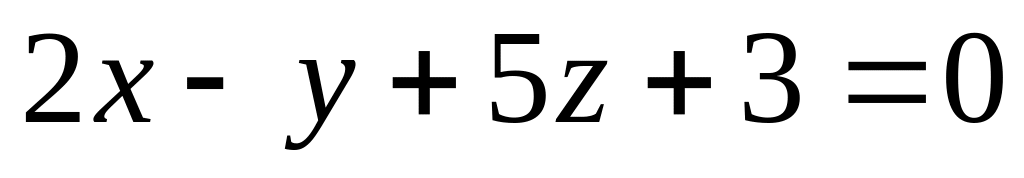 и
и
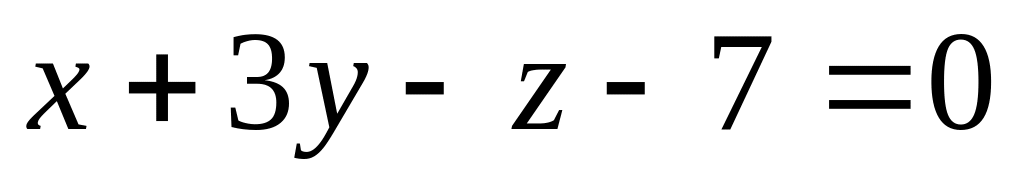
A)
![]() B)
B)![]() C)
C)![]()
D)
![]() E)
E)
![]() .
.
Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, что расстояние между директрисами равно
 и эксцентриситет
и эксцентриситет
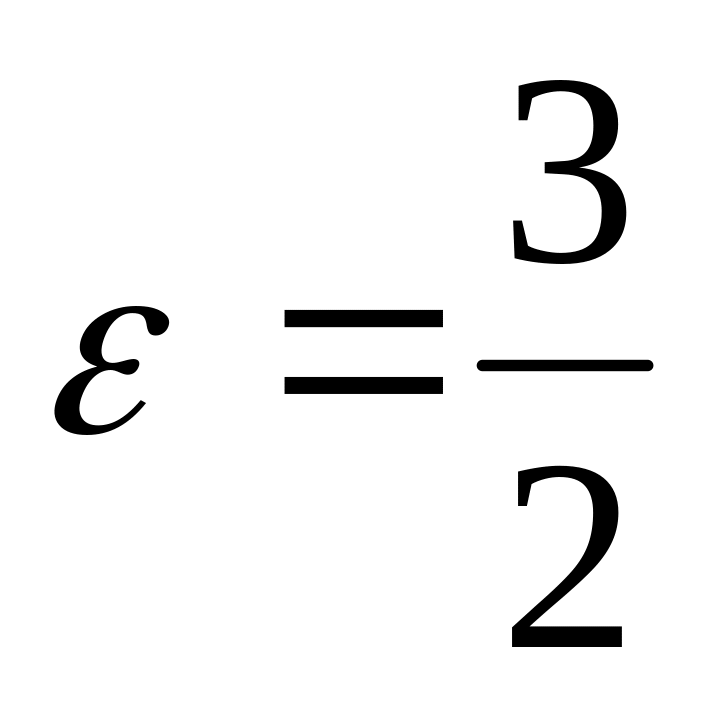
A)
![]() B)
B)![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Найти эксцентриситет эллипса
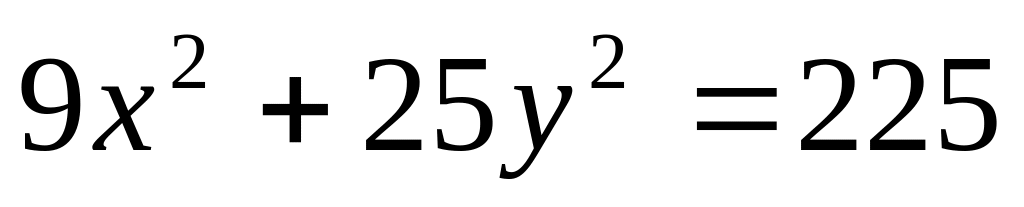
A)
![]() B)
B)![]() C)
C)
![]() D)
D)
![]() E)
E)
![]() .
.
Найти площадь треугольника вершинами, которого
являются точки A(1;1;1), B(2;3;4) ,C(4;3;2).
A)
![]() ,
B)
,
B)
![]() ,C)
,C)
![]() ,
D)
,
D)
![]() , E)
, E)
![]()
Найти длину отрезка отсекаемой прямой
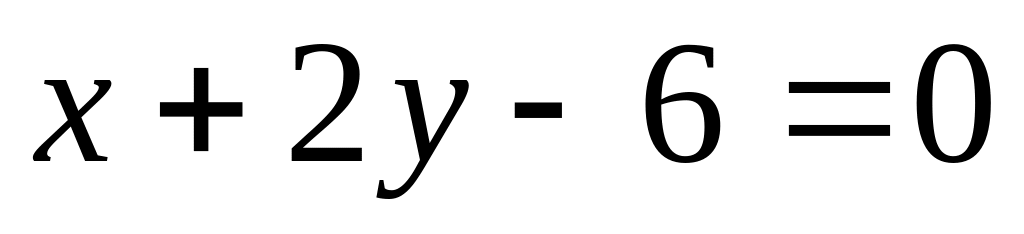 от
оси ординат.
от
оси ординат.
A)3 , B) , C) 2 ,D) -2, E) 4
Найти сумму отрезок отсекаемой прямой
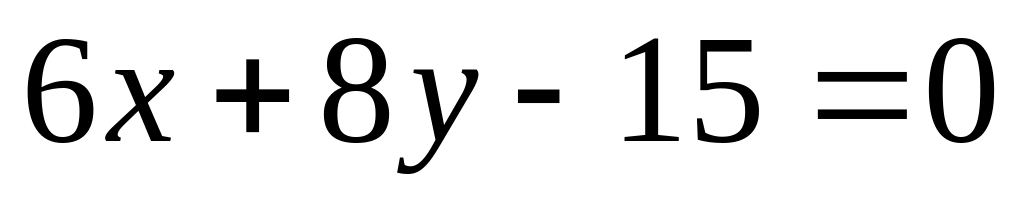 от осей координат.
от осей координат.
A)
2 , B) 3 , C)
![]() ,
D)
,
D)
![]() ,
E) 6
,
E) 6
Найти угол между прямыми
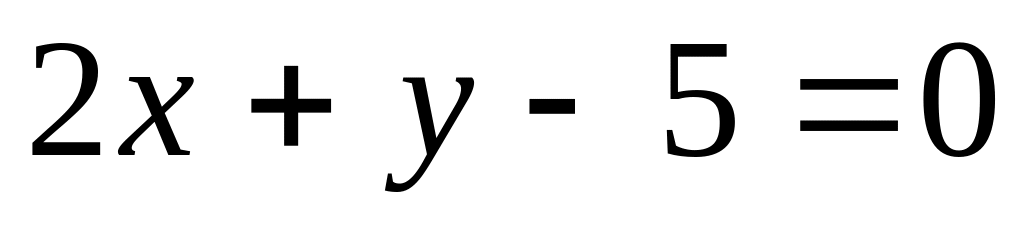 и
и
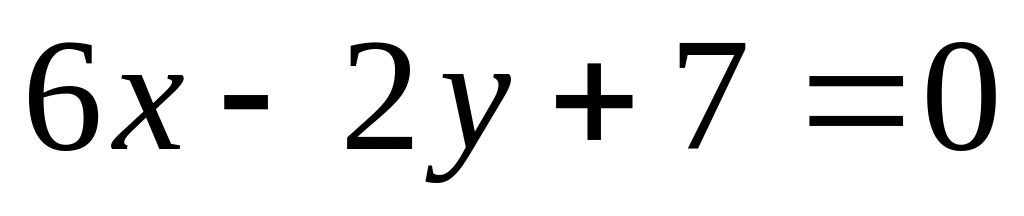
A)
![]() ,
B)
,
C)
,
D)
,
B)
,
C)
,
D)
![]() ,
E)
,
E)
Написать уравнение прямой, проходящей через точку пересечения прямых
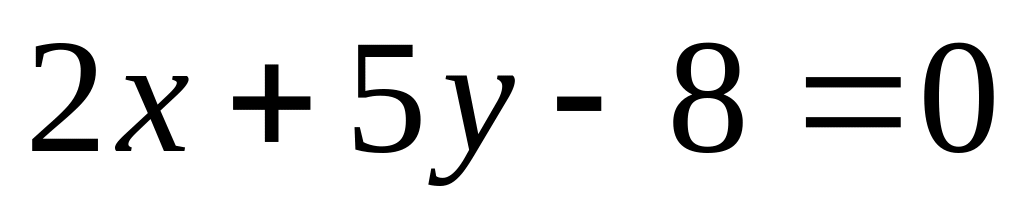 и
и
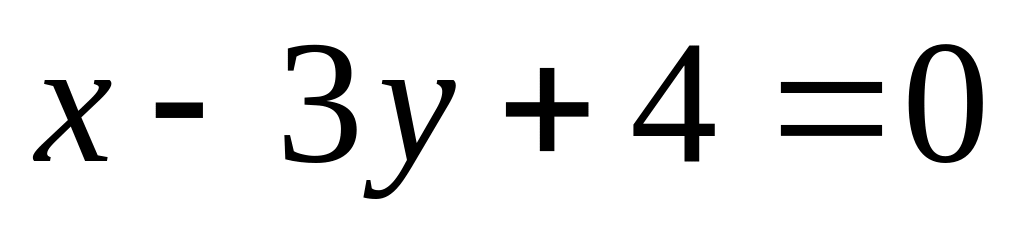 и через точку (4 ; 3) .
и через точку (4 ; 3) .
A) 7x+5y+36=0, B) 17x-40y+52=0, C) 17x-42y+50=0,
D) 5x-7y-36=0, E) 16x-47y-52=0
Привести к нормальному виду уравнение окружности
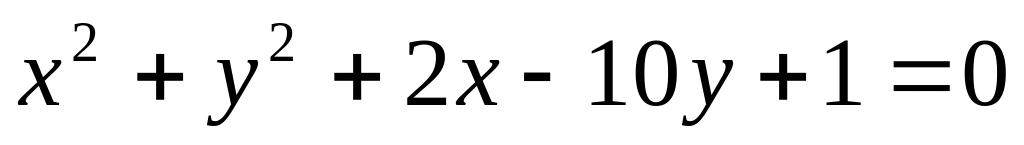 и
найти сумму координатов центра
окружности.
и
найти сумму координатов центра
окружности.
A)4 , B) 2, C) 9 , D) 5, E) 0.
Написать уравнение прямой, проходящей через
точку
M(-2; -5) параллельно
прямой
![]() .
.
A)![]() ,
B)
,
B)
![]() ,
C)
,
C)![]() ,
D)
,
D)![]() ,
E)
,
E)![]()
Найти координаты фокусов гиперболы
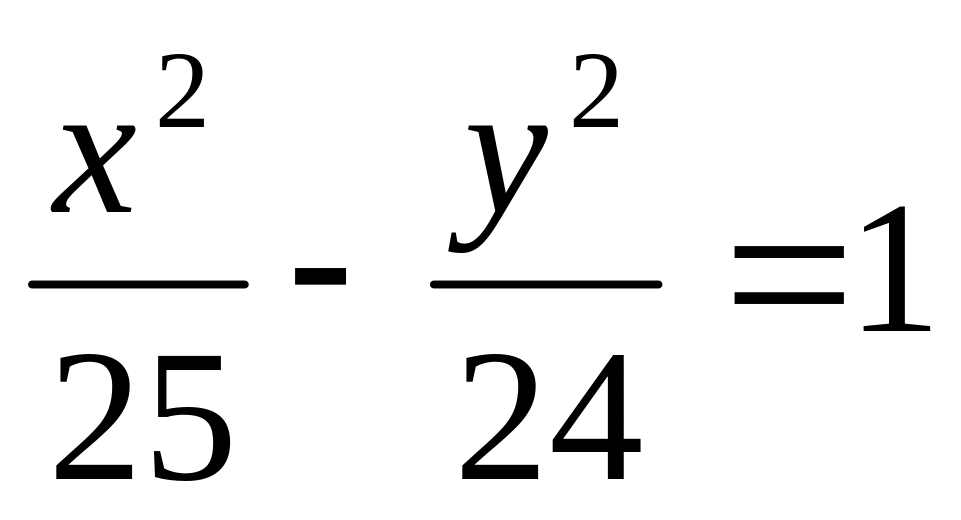 и вычислить сумму
и вычислить сумму
 (где
(где -эксцентриситет
гиперболы).
-эксцентриситет
гиперболы).
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
D)
,
D)
![]() ,
E)
,
E)
![]()
Написать уравнение окружности, проходящей через начало координат и имеющий центр в точке C(6; -8) .
A)
![]() ,
B)
,
B)![]() ,
C)
,
C)
![]() ,
,
D)
![]() ,
E)
,
E)![]()
Найти угол между прямыми
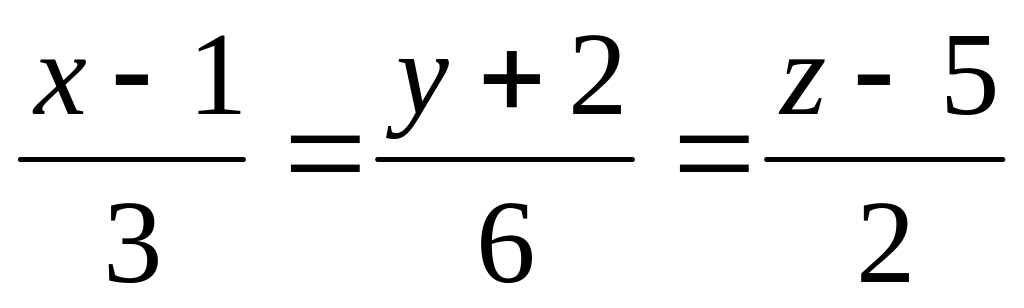 и
и
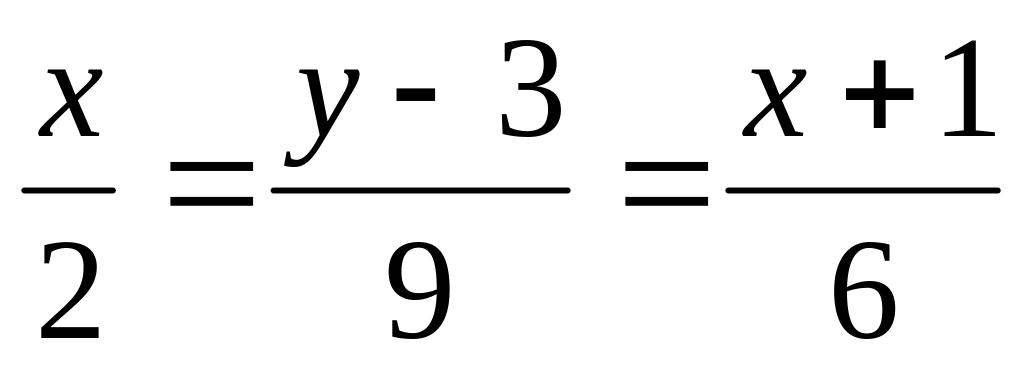 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() , D)
, D)
![]() ,
E)
,
E)
![]()
Найти угол между плоскостями
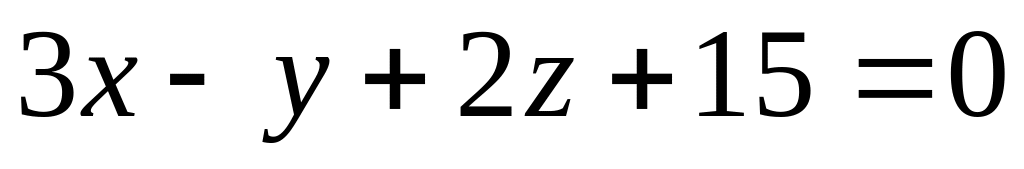 и
и
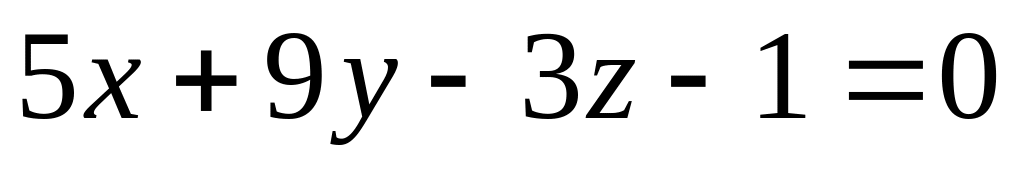 .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
D)
, E)
,
D)
, E)
Найти сумму расстояний отсекаемой плоскостью
![]() от
осей координат.
от
осей координат.
A) 7, B)17, C) 6 , D) 8 , E) 10
Найти сумму расстояний отсекаемой прямой
![]() от осей
координат.
от осей
координат.
A) 10 , B) 8, C) 6, D) 4, E) 12.
Провести прямой через точку M(2;-1) параллельно прямой
![]() и
найти значение свободного члена.
и
найти значение свободного члена.
А) -15, B) 10 , C) -12, D) 14, E) 12.
Написать каноническое уравнение гиперболы,
расстояние
между фокусами равно 26, и эксцентриетет
![]() .
.
A)
![]() , B)
, B)
![]() , C)
, C)
![]() ,
D)
,
,
D)
,
E)
![]()
Написать уравнение прямой
проходящей
через точки![]() и
и
![]() .
.
A)
![]() ,
B)
,
B)
![]() ,
C)
,
C)
![]() ,
,
D)
![]() ,
E)
,
E)
![]()
Написать каноническое уравнение прямой, имеющее следующие параметрическое уравнение
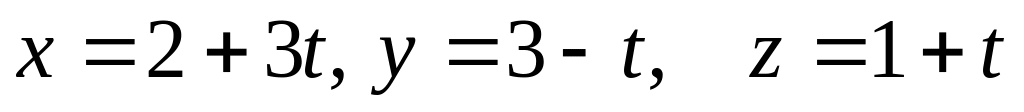
A)
![]() , B)
, B)
![]() ,
C)
,
C)
![]() ,
,
D)
![]() , E)
, E)
![]()
Найти каноническое уравнение гиперболы.
A)
B)
C)
![]()
D)
![]() E)
E)
![]() .
.
