
- •I Элементы линейной алгебры.
- •Матрицы и определители. Векторная алгебра (а).
- •Аналитическая геометрия. (a)
- •3. Введение математического анализа. Функция. Предел и непрерывность (а) (b).
- •4. Производная функции одной переменной и ее приложения (а) (в).
- •Комплексные числа и операции над ними. (а) (в).
- •7. Определенный интеграл и несобственные интегралы. (а) (в).
- •Какие из этих формул написаны правильно?
- •Какие из этих формул написаны правильно?
I Элементы линейной алгебры.
Матрицы и определители. Векторная алгебра (а).
Какие из следующих утверждений можно считать правильным?
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е.
 для
любых
для
любых
 .
.
Для квадратной матрицы А главную диагональ образуют элементы
 .
. является единичной
матрицей n-го
порядка.
является единичной
матрицей n-го
порядка.
 является диагональной
матрицей 3-го порядка.
является диагональной
матрицей 3-го порядка.
Матрица
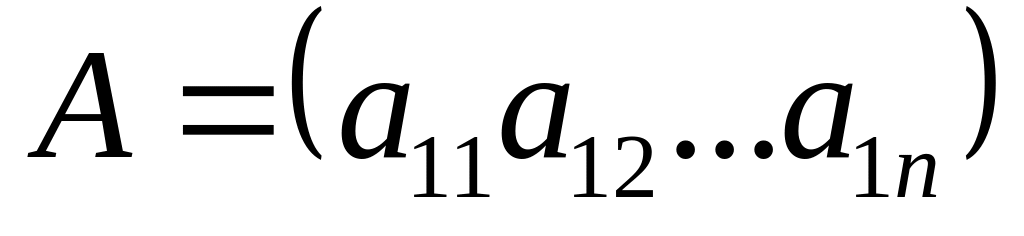 является матрицей – строкой,
является матрицей – строкой,
![]() матрицей – столбцом.
матрицей – столбцом.
А)1,2,3 В) 1,2,4,5 С) 2,3,4 D)1,3,4,5 E)1,3,5.
Какое из этих утверждений является неправильной?
Суммой двух матриц А и В одинакового размера
 называется матрица
называется матрица
 ,
элементы которой
,
элементы которой
 для
.
для
.
Произведением матрицы А на число
 называется матрица
называется матрица
 ,
элементы которой
,
элементы которой
 для
.
для
.
Матрицы любого размера называются нулевой, если все ее элементы равны нулю.
Квадратной матрице n-го порядка содержится
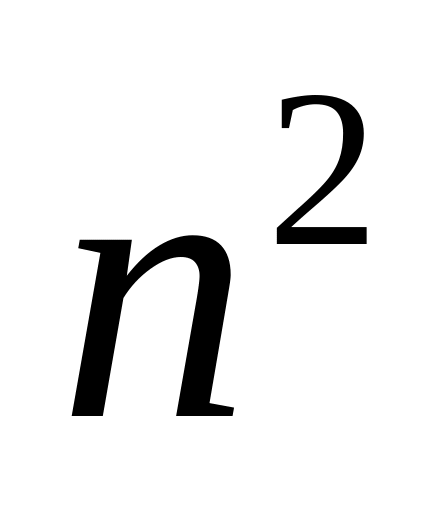 элементов.
элементов.
При умножении матрицу А на матрицу В выполняется условия
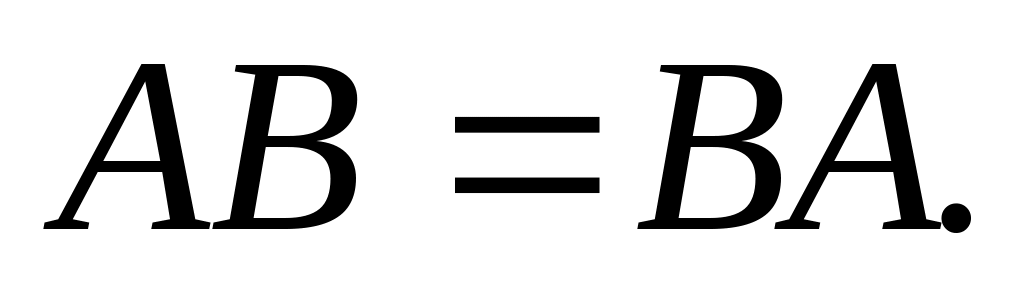
А) 1 В) 5 С)3 D)4 Е) 2.
Какие из этих свойств являются верными для операций над матрицами?
![]()
2)![]()
3)![]()
4)![]()
5)![]()
6)![]()
А) 1,4,5,6 В) 2,4,6 С)1,3,5,6
D)1,2,3,4,5,6 Е)1,4,5,.
Какое из этих свойств не относится к свойствам операции транспонирования матриц?
А)
![]() В)
В)
![]() С)
С)
![]()
D)
Е)
![]() .
.
Какое из этих матриц является треугольной?
А)
![]() В)
В)![]() С)
С)
![]() D)
D)![]() Е)
Е)![]()
Среди этих матриц покажите скалярную
А)
![]() В)
В)![]() С)
С)
![]() D)
D)![]() Е)
Е)![]()
Какие из этих формул написаны правильно?
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
А) 1,2,4,5 В) 2,4,5 С)1,2,3,4,5 D)1,3,5 Е)1,2,5
Какие из этих утверждений являются правильными?
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы;
Обратная матрица
 существует (и единственна) тогда и
только тогда когда исходная матрица
вырожденная.
существует (и единственна) тогда и
только тогда когда исходная матрица
вырожденная.
Обратная матрица существует (и единственна) тогда и только тогда когда исходная матрица невырожденная.
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (или выше) главной диагонали, равны нулю.
Минором
 элемента
элемента
 матрицы
n-го
порядка называется определитель матрицы
матрицы
n-го
порядка называется определитель матрицы
 -
го порядка, полученной из матрицы А
вычеркиванием
-
го порядка, полученной из матрицы А
вычеркиванием
 -
й строки и
-
й строки и
 -
го столбца.
-
го столбца.
Для квадратной матрицы А элементы
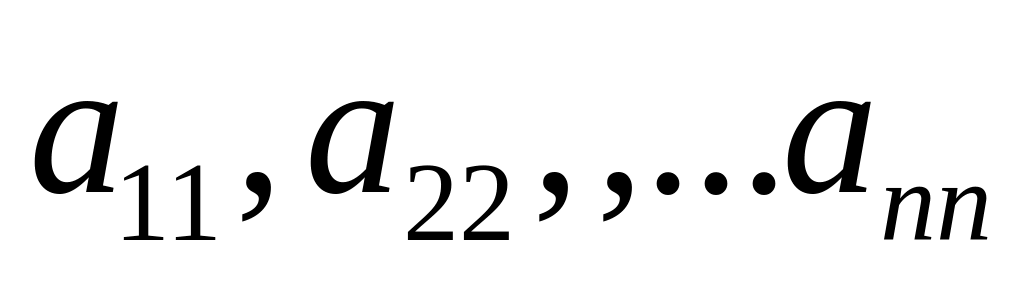 образуют главную диагональ.
образуют главную диагональ.
А) 1,2,3,5 В) 1,3,4,5,6 С)2,4,5,6 D)1,2,4,5,6 Е)1,2,4,6.
Какое из этих утверждений является неправильной?
А) Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0;
В) Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0;
С) Если транспонировать какую-нибудь квадратную матрицу, то ее определитель равен 0.
D) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
Е) При транспонирование матрицы ее определитель не изменяется.
Какое из этих утверждений являются неправильным?
А) Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы;
В) Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений;
С) Ранг матрицы не изменяется при элементарных преобразованиях матрицы;
D) Определитель треугольной (и, очевидно, диагональной)матрицы равен произведению элементов главной диагонали;
Е) Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица вырожденная.
Какое из этих выражений написано неправильно?
А)
![]() - длина вектора
- длина вектора
![]()
В)
![]()
![]() направляющие косинусы вектора
.
направляющие косинусы вектора
.
С)
![]() - единичный вектор вектора
.
- единичный вектор вектора
.
D)
![]() - условия ортогональности векторов
и
- условия ортогональности векторов
и
![]() .
.
Е)
![]() -
условия перпендикулярности векторов
и
.
-
условия перпендикулярности векторов
и
.
Какое из этих утверждений неправильно?
А)
![]() ,
если
,
если
![]() ,
либо
,
либо
![]() ,
либо
,
либо![]() .
.
В)
![]() - векторы
и
коллинеарны;
- векторы
и
коллинеарны;
С)
![]() -
векторы
,
и
-
векторы
,
и
![]() компланарны;
компланарны;
D)
![]() ,
если
,
либо
,
либо
,
если
,
либо
,
либо![]() .
.
Е)
![]() ,
т.е. векторное произведение не обладает
переместительным свойством.
,
т.е. векторное произведение не обладает
переместительным свойством.
Какое из этих выражений не относится к векторному произведению двух векторов и .
А)
![]() (переместительный закон)
(переместительный закон)
В) , если , либо , либо .
С)
![]() (сочетательное свойство по отношению
к скалярному множителю).
(сочетательное свойство по отношению
к скалярному множителю).
D)
![]() ,
где
,
где
![]() -
угол между векторами
и
.
-
угол между векторами
и
.
Е)
![]()
Какие из этих утверждений правильно?
1)
![]() где
-
угол между векторами
и
.
где
-
угол между векторами
и
.
2) , где - угол между векторами и .
3) - условия перпендикулярности векторов и .
4) , если , либо , либо .
5) , т.е. векторное произведение не обладает переместительным свойством.
А) 1,3,5 В) 2,3,4,5, С)1,2,3,4, D)2,3,4,5, Е)1,2,3,4,5.
Условием компланарности трех векторов , и является:
А)
![]()
В)
![]()
С)
![]()
D)
![]()
![]()
Е)
![]()
Условием ортогональности двух векторов и является:
А)
В)
![]() С)
D)
С)
D)
![]() Е)
Е)
![]()
Пусть
 направляющие косинусы вектора. Какая
из нижеследующих формул является
верной?
направляющие косинусы вектора. Какая
из нижеследующих формул является
верной?
A)

B)
![]()
C)
![]()
D)
![]()
Е)
![]()
Пусть ненулевые векторы
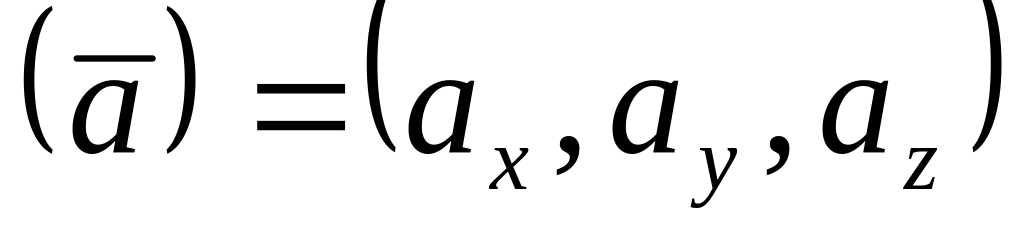 и
и
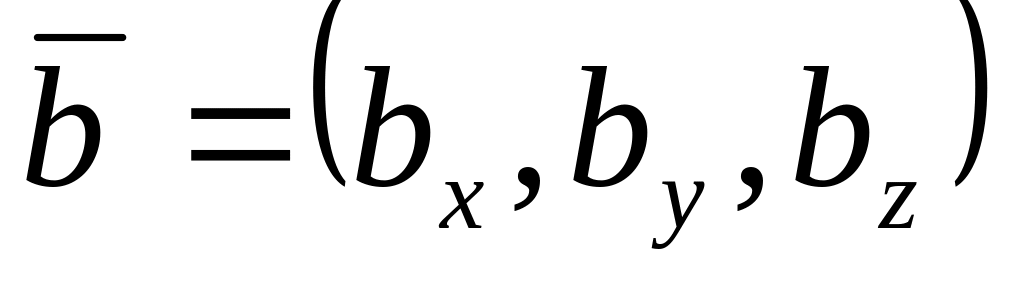 коллинеарны. Какая из нижеследующих
формул является не верной?
коллинеарны. Какая из нижеследующих
формул является не верной?
A)
![]() B)
B)![]() C)
C)
![]() - скалярный множитель
- скалярный множитель
D)
![]() E)
E)![]() .
.
Пусть
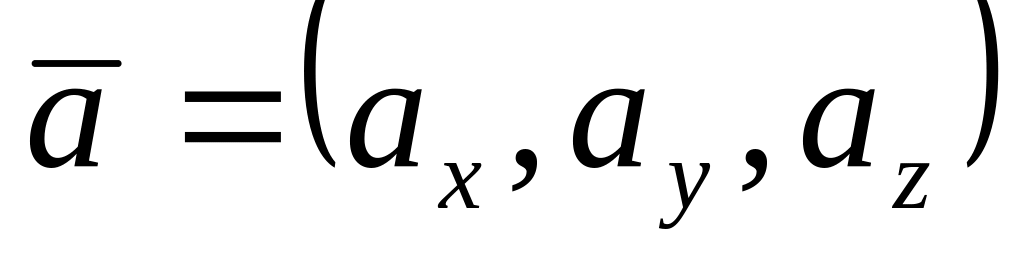 .
Какая из нижеследующих формул является
верной?
.
Какая из нижеследующих формул является
верной?
A)
![]()
![]()
B)
C)
![]()
D)
![]()
E)
![]()
Какая из нижеследующих формул для векторного произведение векторов является не правильной?
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
Для двух векторов и условия является:
А) условием ортогональности;
В) условием коллинеарности;
С) условием аддитивности;
D) Условием коммутативности;
Е) условием компланарности;
Какое из этих утверждений является правильной?
А)
![]() - векторное произведение двух векторов
- векторное произведение двух векторов
В)
![]() - угол между прямой и плоскости;
- угол между прямой и плоскости;
С) если
![]() ,-
T
о
и
является
коллинеарными векторами;
,-
T
о
и
является
коллинеарными векторами;
D) - условие коллинеарности двух векторов;
Е) условие коллинеарности двух векторов.
Формула
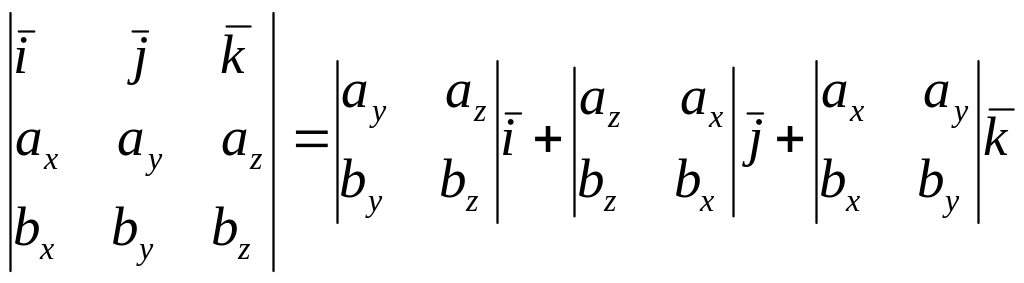 характеризует:
характеризует:
А) скалярное произведение двух векторов;
В) смешанное произведение трех векторов;
С) векторное произведение двух векторов;
D) условию компланарности трех векторов;
Е) условию коллинеарности двух векторов.
Равенство
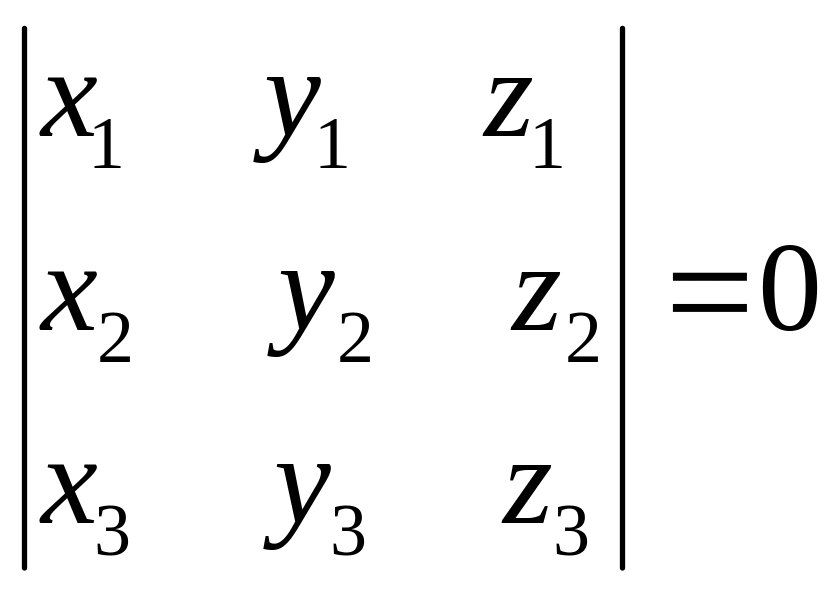 характеризует:
характеризует:
А) условию коллинеарности двух векторов;
В) условию компланарности трех векторов;
С) векторное произведение двух векторов;
D) условию ортогональности трех векторов;
Е) смешанное произведение трех векторов.
Матрицы и определителители. Векторная алгебра (В).
Решить систему уравнений
![]()
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
система не совместна.
E)
система не совместна.
Вычислить определитель.
![]()
A) 22 B) 31 C) 68 D) -3 E)0.
Решить систему уравнений
![]()
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)![]() .
.
Даны матрицы
 и
и
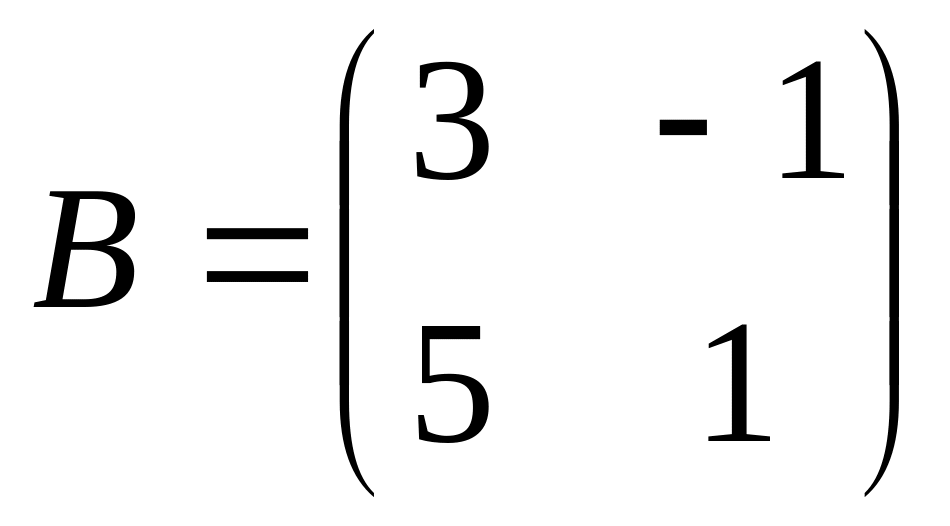 .
Найти
.
Найти
 .
.
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)![]() .
.
Определить ранг матрицы

A) 1 B) 2 C) 3 D) 4 E) 5.
Дана матрица
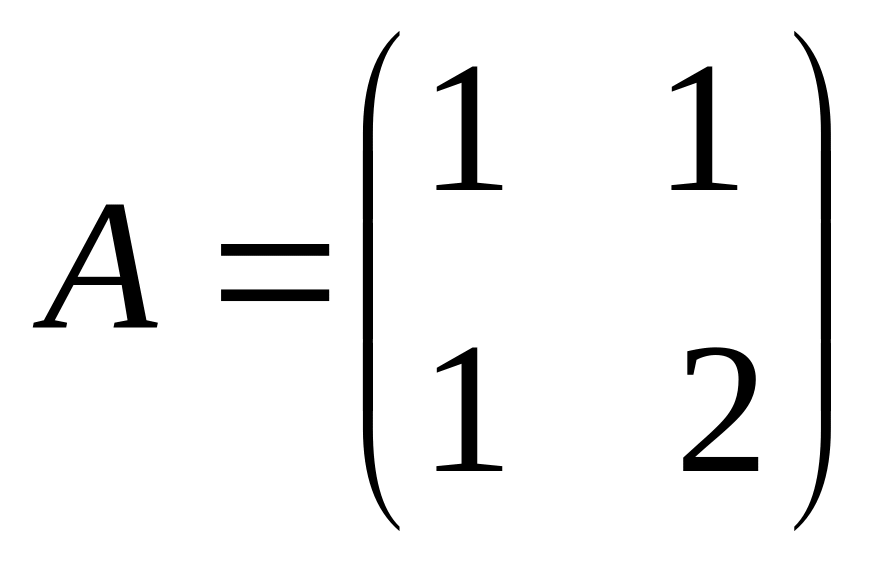 Найти обратную матрицу
Найти обратную матрицу
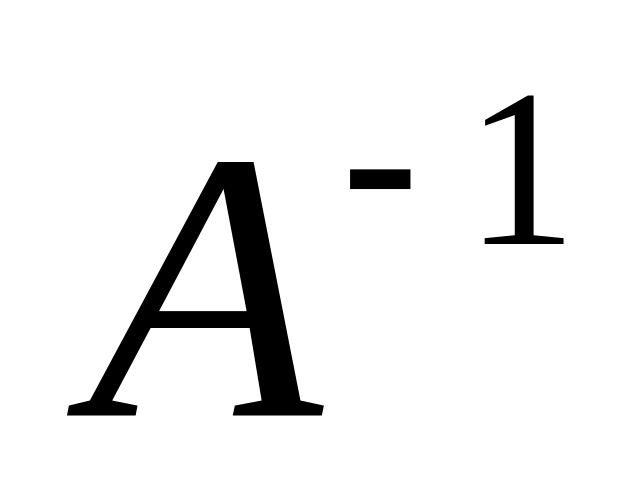 .
.
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)![]() .
.
При каком значении
 векторы
векторы
 и
и
 перпендикулярны.
перпендикулярны.
A) 5 B) -5 C) 0 D) 7 E) -7.
Найти векторное произведение векторов
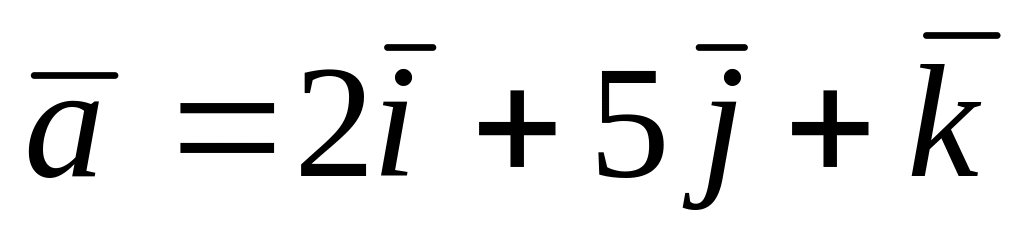 и
и

A)
![]() B)
B)
![]() C)
C)![]() D)
D)
![]() E)
E)![]() .
.
Найти смешанное произведение векторов

A) 0 B) 1 C) 2 D) -1 E) -2.
Найти скалярное произведение векторов
 и
и
 если
если
 и
и

A) 10 B) 6 C) 8 D) -2 E) 0.
Определить ранг матрицы

A) 0 B) 1 C) 2 D) 3 E) 4.
Найти угол между векторами
 и
и
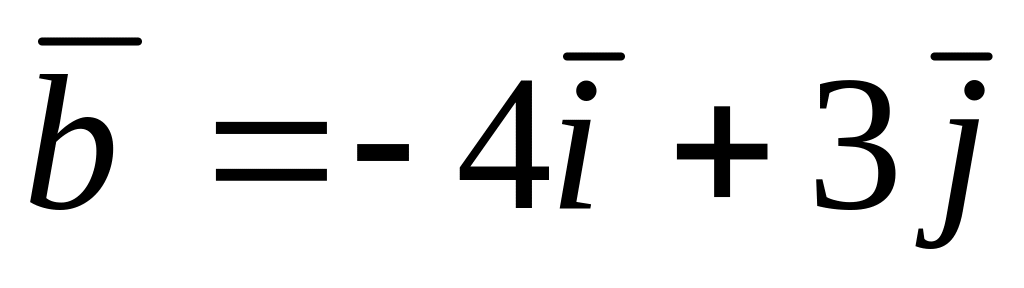
A)
![]() B)
B)
![]() C)
C)
![]() D)
D)![]() E)
0.
E)
0.
Вычислить определитель

A) 4 B) 3 C) -2 D) 0 E) 16.
Найти смешанное произведение векторов

A) 1 B) 2 C) 0 D) -5 E) -1.
Даны матрицы
 и
и
 .
Найти
.
Найти
 .
.
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Решить систему уравнений
![]()
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Решить систему уравнений
![]()
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Вычислить определитель
![]()
A) 14 B) 12 C)3 D) -2 E) 100
Решить систему уравнений
![]()
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Даны матрицы
 и
и

Найти
![]()
A)![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() E)
E)
![]()
Определить ранг матрицы

A) 1 B) 2 C) 3 D) 4 E) 5
Дана матрица
 .
Найти обратную матрицу
.
Найти обратную матрицу
A)
![]() B)
B)
![]() C)
C)
![]() D)
E)
D)
E)
![]()
При каком значение векторы
 и
и
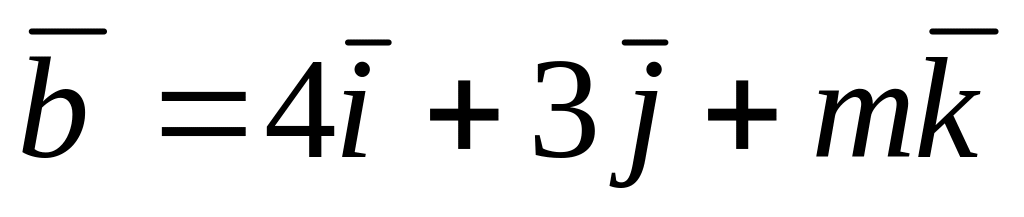 перпендикулярны?
перпендикулярны?
A) 3 B) -3 C) 0 D) 10 E) -10
Найти векторное произведение векторов
 и
и

A)
![]() B)
B)
![]() C)
D)
C)
D)
![]() E)
E)
![]()
Найти смешанное произведение векторов
![]() и
и
![]()
A) 1 B) 2 C)-1 D) 0 E) 11
Найти скалярное произведение векторов
 и
и
 если
если
и
![]()
A) 6 B) 8 C) 0 D) 1 E) -1.
Определить ранг матрицы

A) 0 B) 1 C) 2 D) 3 E) 4.
Найти угол между векторами
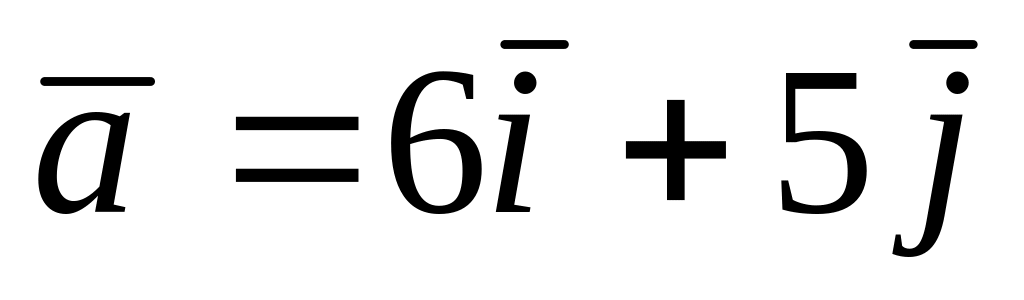 и
и

A)
B)
C)
0
D)
E)
![]()
Вычислить определитель

A) 1 B) -1 C) 3 D) 11 E) 0
Найти смешанное произведение векторов
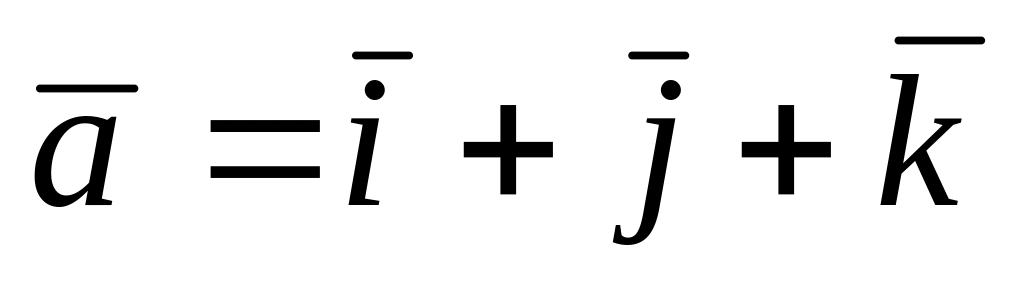 ,
,
 ,
,
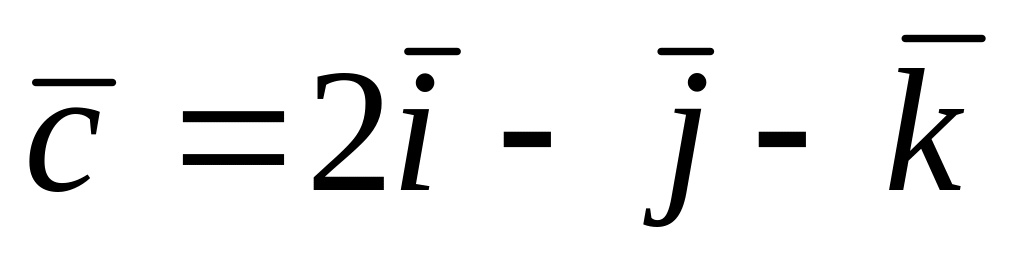
A) 0 B) -1 C) 16 D) 15 E) -4
Даны матрицы
 и
и
 .
Найти
.
Найти
 .
.
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]()
Решить систему уравнений
![]()
A)(1, 4, -5) B) (0, 0, 0) C) (6, -13, -1)
D) (-3, -3, 1) E) (3, -5, 13)
Решить уравнение
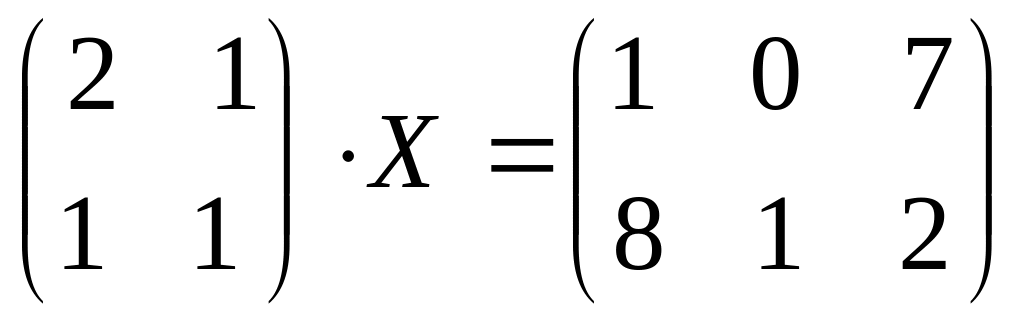
A)![]() B)
B)
![]() C)
C)![]()
D)
![]() E)
E)
![]() .
.
Найти произведение матриц:
![]()
A)![]() B)
B)
![]() C)
C)![]() D)
D)
![]() E)
E)![]() .
.
Найти ранг матрицы:
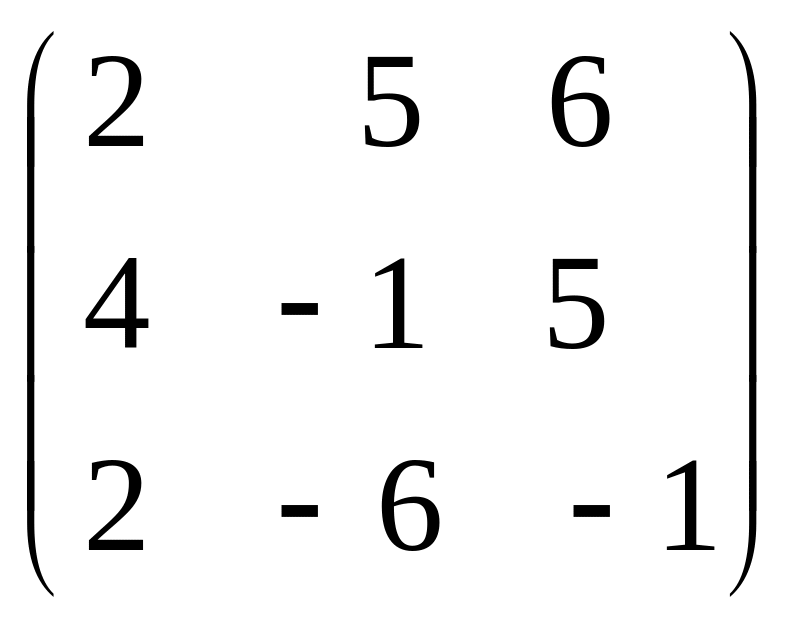
A)
3
B)1
C)2
D)4
E)
![]() .
.
Найти вектор
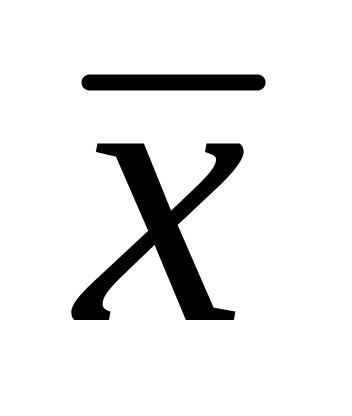 ,
коллинеарный вектору
,
коллинеарный вектору
 и удовлетворяющий условию
и удовлетворяющий условию

A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Найти орт вектора
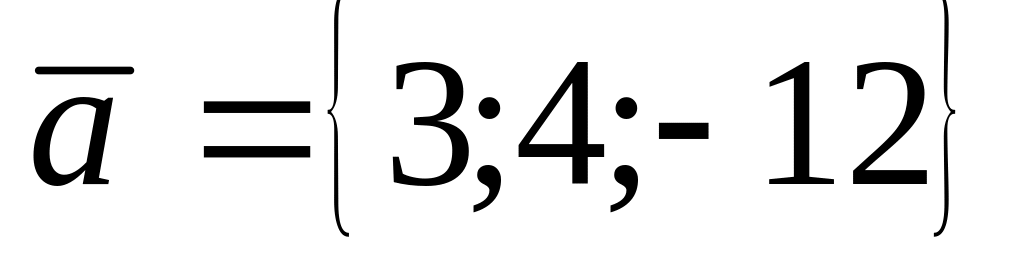
A)
![]() B)
B)
![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
Решить уравнение:

A)
![]() B)
B)![]() C)
C)![]()
D)![]() E)
E)
![]() .
.
Решить уравнение:
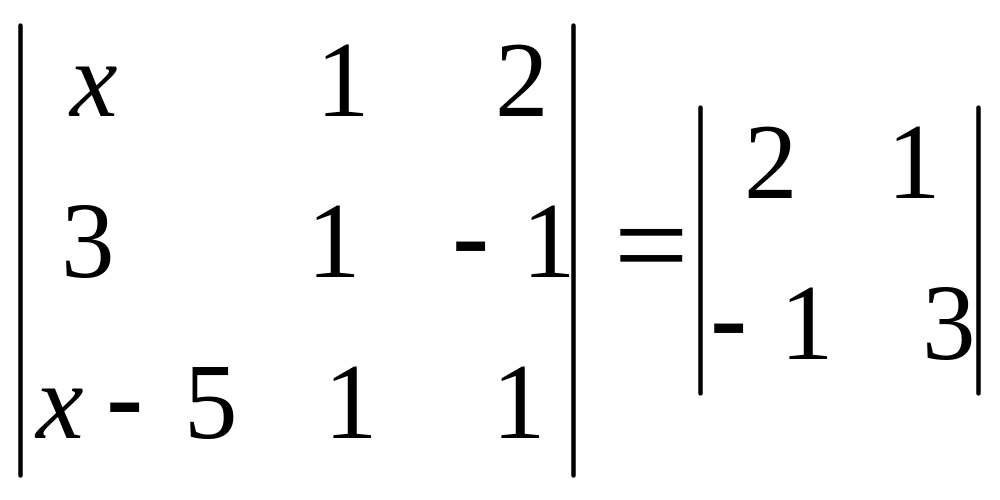
A) 5 B)1 C)11 D)0 E) -4.
Найти векторное произведение
 ,
если
,
если
 и
и
 .
.
A)
![]() B)
B)![]() C)
C)
![]()
D)
![]() E)
E)
![]() .
.
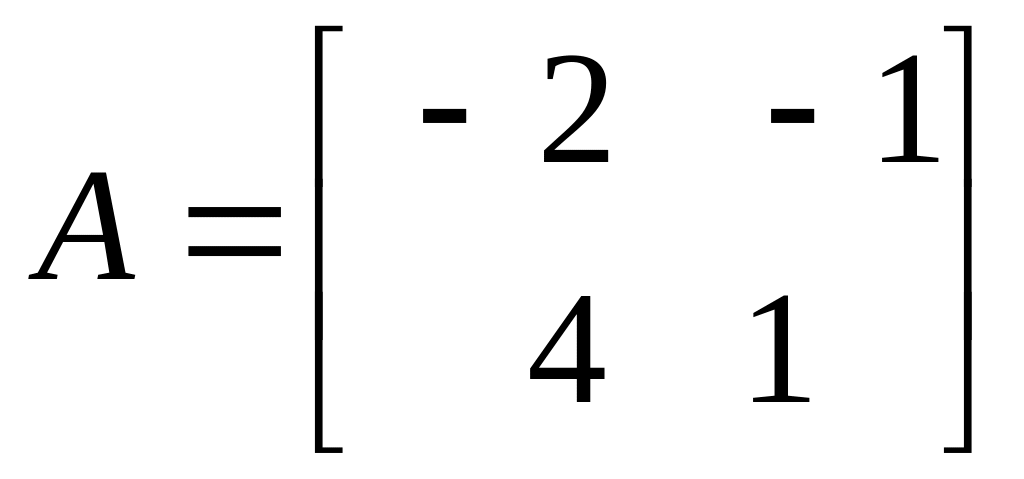 Найти
Найти
A)
 ,B)
,B)![]() ,C)
,C)![]() ,D)
,D)![]() ,E)
,E)
 Найти
.
Найти
.
A)
![]() ,B)
,B)
![]() ,C)
,C)![]() , D)
, D)![]() ,E)
,E)
![]()
Решить систему уравнений
 найти сумму корней.
найти сумму корней.
A)![]() , B) 4 , C) 2 , D)
, B) 4 , C) 2 , D)
![]() ,E) 3
,E) 3
Решить систему уравнений
 найти сумму корней.
найти сумму корней.
A)
![]() , B)
, B)
![]() ,
C)
,
C)
![]() , D)
, D)
![]() ,
E)
,
E)
![]()
 решить
матричное уравнение.
решить
матричное уравнение.
A)
![]() ,
B)
,
B)
![]() , C)
, C)
![]() , D)
, D)
![]() , E)
, E)
![]()
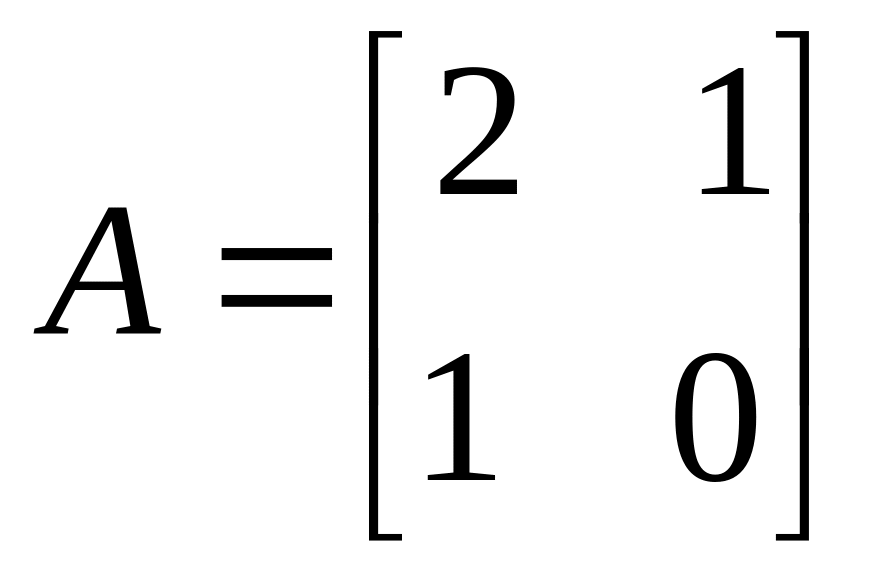 Найти
Найти
 .
.
A)
![]() , B)
, B)
![]() ,
C)
,
C)
![]() , D)
, D)
![]() ,E)
,E)
![]()
 Найти
.
Найти
.
A)![]() , B)
, B)
![]() , C)
, C)
![]() , D)
, D)![]() , E)
, E)
![]()
Найти ранг матрицы
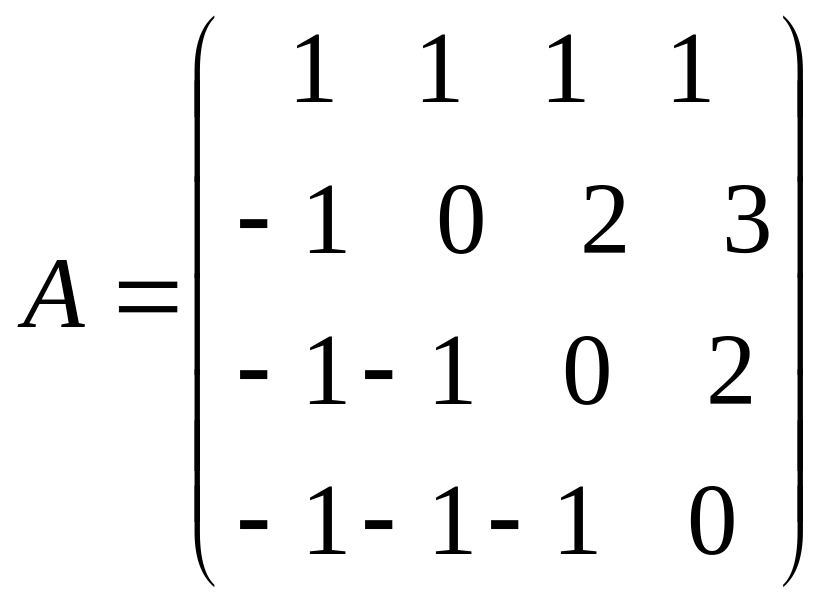 .
.
A) 1 , B) 3 , C) 4 , D) 2, E) 5
Решить систему уравнений
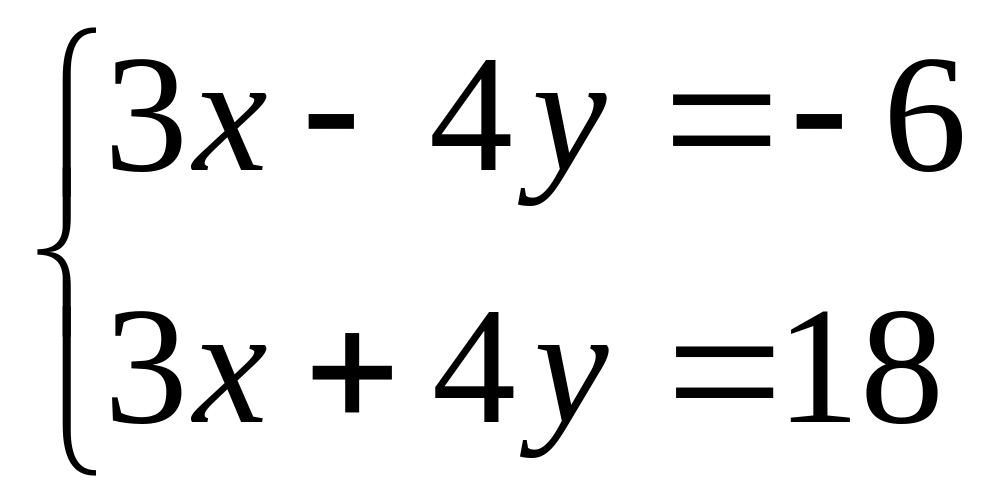 Найти
Найти .
.
8 , B) 5, C) 13 , D)7 , E) 4
