3 Семестр, направление 080.200 Менеджмент

1. Обыкновенное дифференциальное уравнение 1-ого порядка: общее и частное решения. ОДУ с разделяющимися переменными.

2. Однородное дифференциальное уравнение, метод интегрирования.

3. Дифференциальное уравнение, приводяшееся к однородному.

4. Уравнение Бернулли, метод интегрирования.

5. Линейное диференциальное уравнение 1-го порядка. Метод вариации произвольных постоянных.

6. Линейное диференциальное уравнение 1-го порядка. Метод Бернулли.

7. Линейное диференциальное уравнение п-го порядка. Случаи интегрируемости.

8. Линейное диференциальное уравнение п-го порядка с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения однородного уравнения.

9. Линейное диференциальное уравнение п-го порядка с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения.

10. Системы линейных дифференциальных уравнений. Метод исключения неизвестных.

11. Случайные события. Различные определения вероятности появления случайного события. Элементы комбинаторики.

12. Теорема сложения вероятностей для несовместных и совместных событий.

13. Теорема умножения вероятностей для независимых и зависимых событий.

14.Формула полной вероятности.

15. Формула Бейеса.

16. Формула Бернулли.

17. Локальная и интегральная теоремы Лапласа.

18.Случайная величина. Закон распределения дискретной случайной величины.

19. Интегральная функция распределения вероятностей дискретной и непрерывной случайной величины, ее свойства..

20. Плотность распределения вероятностей непрерывной случайной величины, ее свойства.

21.Математическое ожидание, дисперсия, средне квадратическое отклонение, мода и медиана дискретной и непрерывной случайной величины.

22. Биномиальный закон распределения вероятностей дискретной случайной величины.

23.Закон распределения Пуассона для вероятностей дискретной случайной величины.

24. Геометрическое распределения вероятностей дискретной случайной величины.

25 .Закон равномерного распределения вероятностей непрерывной случайной величины.

26 Показательный закон распределения вероятностей непрерывной случайной величины.

27 Нормальный закон распределения вероятностей непрерывной случайной величины (закон распределения Гаусса). Правило трех сигм.

Примеры. О.Д.У.

1. Проверьте, что функция является частным решением уравнения .

2. Докажите, что сумма частного решения линейного неоднородного ДУ 2-го порядка и соответствующего однородного ДУ является общим решением линейного неоднородного ДУ 2-го порядка.

3. Запишите общее решение линейного ДУ с постоянными коэффициентами

,

если соответствующее характеристическое уравнение имеет корень кратности .

13. Теорема умножения вероятностей для независимых и зависимых событий.

4. Запишите общее решение линейного ДУ с постоянными коэффициентами

,

характеристическое уравнение имеет вещественные и различные корни .

5. Напишите частное решение (с неопределенными коэффициентами) для ДУ

.

6. Напишите частное решение с неопределенными коэффициентами для ДУ

.

7. Напишите частное решение с неопределенными коэффициентами для ду

.

8.Решите ДУ с разделяющимися переменными

8.1)

8.2)

8.3)

9. Решите однородное ДУ:

9.1)

9.2)

9.3)

10. Решите линейное неоднородное ДУ 1-го порядка:

10.1)

10.2)

10.3)

10.4)

10.5)

10.6)

11. Решите линейное однородное ДУ 2-го порядка:

11.1)

11.2)

11.3)

12. Решите задачу Коши для линейного однородного ДУ 2-го порядка:

12.1)

12.2)

12.3)

13. Решите линейное неоднородное ДУ 2-го порядка:

13.1)

13.2)

13.3)

13.4)

14. Решите уравнение Бернулли:

15. Решите ДУ в полных дифференциалах:

16. Решите систему линейных ДУ с постоянными коэффициентами:

Теория вероятностей. Комбинаторика. Вероятностьпоявления случайного события.

17. (Задача Даламбера) Испытание состоит в двукратном подбрасывании монеты. Какова вероятность того, что в результате испытания герб выпадет хотя бы один раз?

18. Брошены 3 монеты. Найти вероятность того, что выпадут два герба.

19. Каждая цифра 1,2,3,4,5 написана на одной карте.Извлекается наугад 3 карточки. Найти вероятность того, что составленное и з них трехзначное число окажется четным.

20. При наборе телефонного номера абонент забыл две последние цифры и набрал их наугад, помня олько, что они нечетные и разные.Найти вероятность того, что номер набран правильно.

21. Внутрь круга радиуса наудачу брошена точка. Найти ероятность того, что точка окажется внутри впмсанного в круг : а) квадрата; б) правильного треугольника; в) правильного шестиугольника (предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения внутри круга).

.

22. В равнобедренный прямоугольный треугольник вписан круг.Наудачу брошена точка. Найти вероятность попадания точки в область треугольника, не принадлежащего кругу.

23. В магазине выставлены для продажи изделий, среди которых изделий не качественные. Найти вероятность того, что среди отобранных изделий будут не качественные.

24. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

25. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?

Несовместные и независимые события

26. На складс трех предприятий поступает продукция 1-го и 2-го сорта.В продукции первого предприятия содержится 15%второсортных изделий, в продукции второго предприятия-25%, в продукции третьего предприятия-30%. Чему равна вероятность того, что среди трех изделий (по одному из продукции каждого предприятия) окажутся первосортными два изделия.

27. В урне находится 12 шаров: 8 белых и 4 красных. Какова вероятность того, что выбранные наугад 2 шара будут одного цвета.

28. Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на первый и второй вопросы одинаковы и равны 0.9, на третий- 0.8. Найти вероятность того, что студент ответит: а) на все вопросы; б) по крайней мере, на два вопроса.

Условная вероятность.Формула Байеса.

29. 1/3 ламп производится на 1-ом заводе, 1/4 - на 2-ом, остальные- на 3-ем. Вероятности брака в продукции 1-го, 2-ого,3-его заводов соответственно равны 0.2, 0.15 и 0.05. Найдите вероятность того, что бракованная лампа произведена соответственнона 1-м, 2-ом или 3-ем заводе.

30. Два производственных участка по выпуску однотипной продукции за смену выдали одинаковое количество изделий. Возможный процент брака на первом участке составляет 5%, на втором-4%. Найти вероятность того, что наудачу взятая деталь, из числа поступивших за смену, не соответствует установленным требованиям.

Формула полной вероятности.

31. На склад поступило 1500 изделий с 1-ой фабрики и 2000 изделий со 2-ой. Известно, что средний процент нестандартных изделий среди продукции 1-ой фабрики равен 3%, 2-ой- 2%. Найти вероятность того, что наудачу взятое со склада изделие будет нестандартным.

Формула Бернулли.

32. В магазине 5 холодильников. Вероятность выхода из строя каждого холодильника в течение года равна 0.2. Найти вероятность того, что в течение года ремонта потребует:

1) 4 холодильника; 2) не менее 2-х холодильников; 3) не более 1 хододильника; 4) не менее 1 холодильника.

33. Вероятность того, что изделие является дефектным, равна 0.1. Сколько надо выбрать изделий, чтобы среди них с вероятностью более 0.96 оказалось хотя бы одно дефектное?

34. Найти вероятность наступления события ровно 3 раза в пяти независимых испытаниях, если вероятность появления этого события в каждом испытании равна .

Дискретная случайная величина: примеры решений задач.

35. В магазине имеется 15 автомобилей определенной марки. Среди них 7 черного цвета,

6 серого и 2 белого. Представители фирмы обратились в магазин с предложением о продаже им 3 автомобилей этой марки, безразлично какого цвета. Составьте ряд распределения числа проданных автомобилей черного цвета при условии, что автомобили отбирались случайно.

36. В городе 4 коммерческих банка. У каждого риск банкротства в течение года

составляет 20%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.

37. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины – числа импортных из четырех наудачу выбранных телевизоров. Найти функцию распределения этой случайной величины и построить ее график.

Непрерывная случайная величина: примеры решений задач.

38. Случайная величина задана дифференциальной функцией распределения 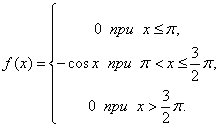 1) Определить вероятность попадания случайной величины X в интервал [π,5/4π]. 

2) Найти математическое ожидание и дисперсию случайной величины X. 

39. Случайная величина X задана плотностью вероятности: 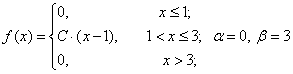 Требуется:  а)найти коэффициент C;  б) найти функцию распределения F(x);  в) найти M(X), D(X), σ(X)  г) найти вероятность P(α < X < β);  д) построить графики f(x) и F(x). 

40. Случайная величина Х задана функцией распределения F(x).  А) является ли случайная величина Х непрерывной? Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.  В) постройте схематично графики f(X) и F(X). 

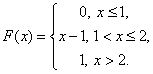
41. Дана функция распределения F(x) непрерывной случайной величины X.  1. Найти значения параметров a,b  2. Построить график функции распределения F(x)  3. Найти вероятность P(α < X < β) 4. Найти плотность распределения p(x) и построить ее график. 

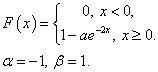
42. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e^-2t при t ≥ 0 и f(t)=0 при t<0.  1) Найти формулу функции распределения этой случайной величины.  2) Определить вероятность того, что прибор проработает не более года.  3) Определить вероятность того, что прибор безотказно проработает 3 года.  4) Определить среднее ожидаемое время безотказной работы прибора. 

Министерство образования и науки РФ

УНИВЕРСИТЕТ МАШИНОСТРОЕНИЯ

Кафедра «Математический анализ»

Дисциплина «Математика»

Для студентов 3 семестра

Направление 080200.62 (ЭФМ)

БИЛЕТ №1

1. Линейное диференциальное уравнение 1-го порялка. Метод Бернулли.