Раздел I Общие сведения по геодезии
Тема 1.1. Понятие о фигуре и размерах Земли
Поверхность Земли общей площадью 510 млн. км2 разделяется на Мировой океан (71%) и сушу или материки (29%).
Так как геодезические работы выполняют с целью измерения участков на земной поверхности, а затем изображают их на бумаге, то нужно иметь понятие о форме и размерах Земли.
Если мысленно продолжить поверхность морей и океанов в их спокойном состоянии под сушей, то получим уровенную поверхность, которая в каждой своей точке перпендикулярна к отвесной линии, т.е. к направлению линии силы тяжести.
Фигура Земли, ограниченная уровенной поверхностью, совпадающей с поверхностью Мирового океана и продолженная под материками, называют геоидом (рис.1.1.).
Средний уровень Балтийского моря, отмеченный чертой Кронштадтского футштока (футшток – в данном случае медная доска с горизонтальной чертой, замурованная в гранитный устой моста Обводного канала) принят за исходную уровенную поверхность, от которой отсчитывают высоты точек земной поверхности. Поэтому в нашей стране система высот получила название Балтийская система высот.
1. Мировой океан 2. Земной эллипсоид 3. Отвесные линии 4. Тело Земли 5. Геоид
Поверхность геоида из-за влияния центробежной силы и неравномерного распределения масс внутри Земли геометрически неправильна и не может быть выражена математической формулой. Поэтому за форму Земли принимают эллипсоид вращения или сфероида, который имеет наименьшее отклонение от поверхности геоида.
Размеры
земного эллипсоида характеризуются
длинами его полуосей а
(большая полуось) и b
(малая полуось). Вследствие вращения
земного эллипсоида приплюснут с полюсов
и отношение
называется сжатием
эллипсоида.
Линии пересечения поверхности эллипсоида плоскостями, проходящими через ось вращения Земли (РР1), называются меридианами и представляют собой эллипсы.
Линии пересечения поверхности эллипсоида плоскостями, перпендикулярными к оси вращения Земли, называются параллелями и являются окружностями.
Параллель, плоскость которой проходит через центр сфероида, называется экватором.
Рис. 1.2. Земной эллипсоид.
В 1940 г. советскими учеными под руководством проф. Ф.Н. Красовского и А.А. Изотова были получены размеры эллипсоида, наиболее подходящие для территории СССР (а = 6 378 245 м, b = 6 356 863 м, α = 1:298,3). Радиус такой сферы для эллипсоида Красовского R= 6371,11 км.
Для решения многих практических задач сжатие земного эллипсоида не учитывают и фигуру Земли за шар радиусом 6370 км.
Тема 1.2. Метод проекций в геодезии.
При изображении на бумаге пространственных форм земной поверхности в геодезии пользуются ортогональной (прямоугольной) проекцией. При изображении больших территорий земной поверхности проектирование производится на уровенную поверхность Земли.
Пусть поверхность Р (рис. 1.3.,а) является частью уровенной поверхности земли. Точки А, В, С и D, расположенные в характерных точках физической поверхности Земли на значительных расстояниях друг от друга, проектируются отвесными линиями на уровенную поверхность Р. Пересечение отвесных линий с поверхностью Р дает проекции точек А, В, С, D на этой поверхности (а, b, c, d). Тогда положение точек а, b, c, d на уровенной поверхности Земли может быть определено координатами (географическими или прямоугольными) в системе координат, оси которой расположены на поверхности Р.
Положение точек земной поверхности А, В, С и D определится соответствующими географическими или прямоугольными координатами и длинами отвесных линий (aА, bВ, cС, dD) от уровенной поверхности до точек физической поверхности Земли, которые называются высотами.
Высоты бывают абсолютные, если их отсчет ведется от уровенной поверхности Земли Р, и условные (относительные), если их отсчет ведется от произвольной уровенной поверхности Р1, параллельной поверхности Р.
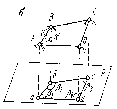
Рис. 1.3. Проекции точек земной поверхности: а) на уровенную поверхность; б) на горизонтальную плоскость.
Обычно за начало отсчета абсолютных высот принимают уровень океана или открытого моря в спокойном состоянии. В России за начало отсчета абсолютных высот принят нуль Кронштадтского футштока (футшток – медная доска с горизонтальной чертой, замурованная в гранитный устой места Обводного канала), соответствующий среднему уровню Балтийского моря по данным многолетних наблюдений. Поэтому система высот в нашей стране получила название Балтийской.
Численное значение высоты называется отметкой точки (абсолютной или условной). Например, НА = 528,752 м – абсолютная отметка точки А; НА′ = 28,752 м – условная отметка той же точки.
Разность высот двух точек (абсолютных или условных) называется превышением h:
