
- •1. Сведем известные данные в исходную таблицу 1.1, дополнив ее двумя графами с вероятностями отсутствия j-ых признаков в I-ых состояниях гтд – ). Эти вероятности определяем по формуле:
- •Задание 2 Построение графиков плотностей распределения диагностического параметра при двух диагнозах объекта.
- •Задание 4 Оценка граничного значения Ko с использованием критерия минимального числа ошибочных решений.
- •Задание 5 Оценка граничного значения Ko с использованием критерия максимального правдоподобия
- •Задание 6 Оценка граничного значения Ко методами итерации и Неймана-Пирсона на эвм.
- •Задание выдал ________________в.З. Чокой________________________
- •Контроль и диагностирование ат при ремонте

Задание 1 Формирование диагностической программы методом Байеса.
Исходные данные по заданию 1.
Значения вероятностей (таблица 1):
Таблица 1
|
|
|
|
|
|
|
|
|
0,26 |
0,39 |
0,46 |
0,25 |
0 |
0,05 |
0,09 |
0,11 |
0,8 |
1. Объект: авиационный газотурбинный двигатель.
2. Признаки: К1 - помпаж двигателя
К2 - повышенный расход топлива.
3. Состояния: D1 - повреждение рабочих лопаток проточной части
D2 - нарушение регулировки топливной аппаратуры
D3 - исправное состояние.
Требуется определить вероятности всех трех диагнозов ГТД при всех возможных сочетаниях признаков. Результаты свести в диагностическую таблицу и сформулировать выводы для последующего использования результатов в эксплуатирующих организациях.
При выполнении задания использовать общую формулу Байеса, при условии полной независимости признаков:
 (1.1)
(1.1)
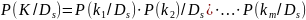 (1.2)
(1.2)
где -
вероятности i-ых
диагнозов ГТД при контроле комплекса
диагностических признаков K;
-
вероятности i-ых
диагнозов ГТД при контроле комплекса
диагностических признаков K;
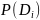 -
вероятности наличия у ГТД i-го
диагноза;
-
вероятности наличия у ГТД i-го
диагноза;
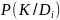 -
вероятность наличия комплекса признаков
у ГТД при
i-ом
диагнозе;
-
вероятность наличия комплекса признаков
у ГТД при
i-ом
диагнозе;
n – число возможных состояний ГТД;
m – число диагностических признаков, включая и случаи отсутствия признаков.
Выполнение задания.
1. Сведем известные данные в исходную таблицу 1.1, дополнив ее двумя графами с вероятностями отсутствия j-ых признаков в I-ых состояниях гтд – ). Эти вероятности определяем по формуле:
 (1.3)
(1.3)
Таблица 1.1
Состояния Di |
Вероятности, известные по результатам наблюдений |
||||
P(k1 / Di) |
P( |
P(k2 / Di) |
P( 2 / Di) |
P(Di) |
|
D1 |
0,26 |
0,74 |
0,25 |
0,75 |
0,09 |
D2 |
0,39 |
0,61 |
0 |
1 |
0,11 |
D3 |
0,46 |
0,54 |
0,05 |
0,95 |
0,8 |
Далее по формулам (1.1 и 1.2) с использованием данных из таблицы 1.1 рассчитываются вероятности диагнозов ГТД при возможных сочетаниях исходов диагностирования (признаков).
2. Определим вероятности диагнозов, когда проявляются оба признака k1 и k2, то есть имеет место диагностическое событие "k1k2":
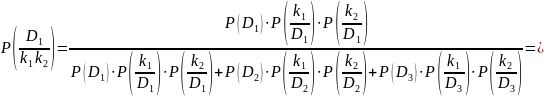
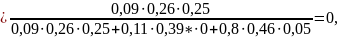 2412
2412

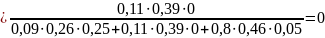


3. Определим вероятности состояний, когда обнаружен признак k2, а признак k1 не наблюдается, то есть имеет место диагностическое событие " 1k2":
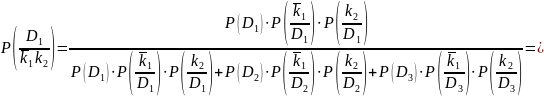
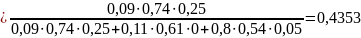


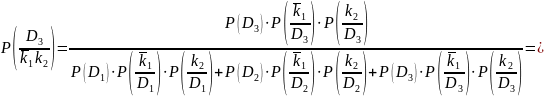

4. Определим вероятности состояний, когда обнаружен признак k1, а признак k2 не наблюдается, то есть имеет место диагностическое событие "k1 2":


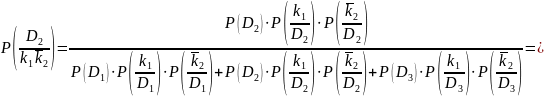


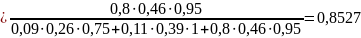
5. Определим вероятности состояний, когда не наблюдаются оба признака k1 и k2, то есть имеет место диагностическое событие " 1 2":
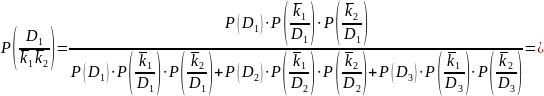
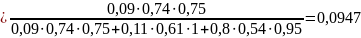

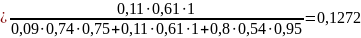
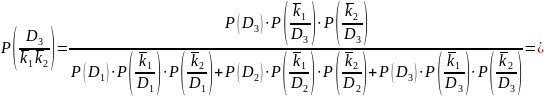

6. Полученные выше результаты расчетов сведем в диагностическую таблицу 2.
Таблица 2 - Диагностическая таблица
Состояния Di |
Вероятности состояний при различных вариантах исходов диагностирования |
|||
P(Di / k1k2) |
P(Di / 1k2) |
P(Di / k1 2) |
P(Di / 1 2) |
|
D1 |
0,2412 |
0,4353 |
0,0428 |
0,0947 |
D2 |
0 |
0 |
0,1046 |
0,1272 |
D3 |
0,7588 |
0,5647 |
0,8527 |
0,778 |
Выводы.
1. Исходя из диагностической таблицы 2 контроль признаков k1 и k2 с высокой вероятностью (P(Di/k1 2) = 0,8527) обеспечивает возможность выявление исправного состояния (диагноза) D3.
2. Выявление неисправного состояния D1 (повреждение рабочих лопаток проточной части) и неисправного состояния D2 (нарушение регулировки топливной аппаратуры) при любых комбинациях исходов диагностирования проблематично, так как уровень рассчитанных вероятностей низкий. Для выявления состояния D1 и состояния D2 необходим контроль дополнительных признаков.



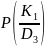
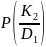

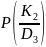
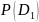

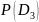
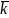 1
/ Di)
1
/ Di)