Тема 4. Понятие сигнала и его модели. Формы представления детерминированных сигналов: временная, частотная и векторная (геометрическая).
Цель лекции:
1. Понятие сигнала и его модели.
2. Формы представления детерминированных сигналов.
3. Временная форма представления сигнала
Вопросы:
1. Что понимают под детерминированным сигналом.
2. Разновидности математических представлений детерминированных сигналов.
3. Запишите условия ортонормированности и ортогональности системы функций.
4. Почему необходимо изучение моделей детерминированных сигналов..
5, Опишите временную форму представления сигналов.
1. Понятие сигнала и его модели.
Сигнал — материальный носитель информации специально создаваемый для передачи сообщения в информационной системе.
В качестве носителей информации используются колебания.
Детерминированные колебания определены в любые моменты времени.
Случайные колебания могут иметь параметры, значение которых предсказать невозможно.
Сигнал представляет собой случайное колебание.
Но изучение моделей детерминированных сигналов необходимо:
1) Так как случайный процесс может быть представлен набором детерминированных функций.
2) Детерминированные сигналы специально создаются для целей измерения, наладки, регулирования объектов информационной техники
.
2 Формы представления детерминированных сигналов.
Детерминированный сигнал может быть представлен:
а) непрерывной функцией непрерывного аргумента см. Рис. 1
u(t) !
!
!____________________________t.
!
!
!
Рис.1
б) непрерывная функция дискретного аргумента, на рис.2.
u(t)!
!
!
!___________.l l l t.
!
!
Рис.2
в) дискретной функцией непрерывного аргумента на рис.3
u(t)!................................................
!.................................................
!.................................................
!__________________________ t
!......................................................
!.....................................................
!....................................................
Рис.3
г) дискретной функцией дискретного аргумента, на рис. 4
u(t)!..............................................
!...............................................
!................................................
!__________________________. t
!..................................................
!...................................................
!...................................................
Рис.4
Цель: Найти такое представление сигнала, которое облегчает задачи исследования происхождения реальных сигналов через системы связи.
Предположим, что описание сигнала u(t) удовлетворяет условиям Дирихле (что практически часто соблюдается для реальных сигналов).
Представим
сигнал u(t)
в
виде взвешенной суммы базисных фунций
(t)
:
(5,1)
Если в качестве базисных функций выбираются ортогональные, т.е. такие
на
отрезке, что для всех
кроме, к
=
j
имеет место:
(5.2)
Эта
система фуекций будет ортонармированной,
если для всех
справедливо
соотношение
(5.3)
Определим
коэффициенты
Ск
при представлении сигнала u(t)
совокупностью
ортонормированных функций
в виде (5.1). Правую и левую части уравнения
(5,1) умножим на
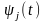-и
интегрируем на интервале [
],
где [
]
[
]
(5,4)
В силу справедливости (5.2) все интегралы в правой части выражени (5.4) при к j будут равны нулю. При к=j в соответствии с (5.3) интеграл равен 1
Сk = u(t)t (t)dt.
Временная форма представления сигнала
Времнным представлением сигнала называется такое разложение сигнала U(t), при котором в качестве базисных функцийиспользуются единичные импульсные функции -дельта-функции:
Символическое расположение дельта-функции показано на рис.5.
t- 1 :
:
t
0
Рис.5
Единственным параметром правильно выражающим реальный сигнал, является время его действия. С помощью - функции значение реального сигнала можно выразить как:
(5.5)
Функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Разложение (5) имеет большое значение в теории линейных систем, т.к. установив реакцию системы на элементарный входной сигнал в виде дельта-функции, можно определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующимзначениям входного сигнала.
Основная литература: 2[18-24]; 6[43-47];
Дополнительная литература: 13(20-23]; 161147-157].
Контрольные вопросы:
1. Что понимают под детерминированным сигналом.
2. Разновидности математических представлений детерминированных сигналов.
3. Запишите условия ортонормированности и ортогональности системы функций.
4. Почему необходимо изучение моделей детерминированных сигналов..
5. Опишите временную форму представления сигналов.