
- •Содержание
- •Раздел 1. Теоретические основы надежности
- •Понятия и определения надежности
- •Показатели надежности
- •Показатели безотказности.
- •Показатели долговечности.
- •Коэффициент технического использования является безразмерной величиной
- •Экономические аспекты надежности
- •Экономические показатели надежности
- •Отказ. Классификация отказов. Параметр потока отказов
- •1) По причинам возникновения:
- •Энергетическая концепция возникновения отказа
- •Случайные величины. Законы распределения, применяемые в теории надежности
- •Определение показателей надежности по эмпирическим данным
- •Интенсивность отказов определяется как:
- •Выбор закона распределения
- •Параметры статистического распределения.
- •Надежность сложных систем. Сложная система и ее характеристики
- •Структурный анализ систем технологического оборудования
- •1) Надежность системы с последовательно включенными элементами всегда будет ниже надежности самого ненадежного элемента системы:
- •2) Чем сложнее система (чем больше элементов в системе) с последовательным соединением элементов, тем ниже ее надежность; при усложнении системы ее надежность будет падать.
- •1) Надежность системы с параллельно включенными элементами будет выше, чем надежность отдельного элемента;
- •2) Надежность системы увеличивается с увеличением числа элементов.
- •Методы расчета надежности сложных технических систем
- •Методика определения надежности сложных систем с помощью минимальных путей и минимальных сечений на примере системы «2 из 3»
- •Резервирование. Методы, способы и типы резервирования
- •Задачи выбора оптимального числа резервных элементов в системе в случае нагруженного резерва
- •Расчет надёжности в случае ненагруженного резерва
- •Классификация машин и аппаратов по надежности
- •Работоспособность: анализ области работоспособности
- •Источники информации по надежности
- •Испытания на надежность: объекты, виды и методы испытаний
- •Раздел 2. Физические основы надежности
- •Старение и износ
- •Модель старения. Законы старения. Законы превращения
- •Процессы старения, протекающие при контакте поверхностей
- •Область существования процесса старения
- •Классификация процессов старения
- •Износ материалов: природа и классификация
- •Классификация видов изнашивания по видам
- •Классификация процессов изнашивания по скорости разрушения
- •Раздел 3. Эксплуатационная надежность
- •Методика определения остаточного ресурса при малоцикловых нагрузках
- •Методика определения остаточного ресурса химического оборудования по критерию коррозионной стойкости
- •2.1. Определение минимального числа точек поверхности для измерений
- •2.1.А. Достоверность расчета надежности
- •2.1.Б. Оценка однородности выборки
- •2.2. Определение параметров распределения глубин разрушения
- •2.3. Определение максимальной глубины разрушения
- •3.1. Расчет ресурса Тр в частном случае при постоянной скорости разрушения с
- •3.2. Расчет минимального установленного ресурса
- •3.3. Расчет остаточного установленного ресурса
Определение показателей надежности по эмпирическим данным
1 В случае малой выборки вероятность отказа в i-й по порядку момент появления отказа ti оценивается как:
![]() ,
,
где n – объем выборки.
Оценка вероятности безотказной работы определяется:
P(ti)=1
- F(ti) =
![]() .
.
Интенсивность отказов определяется как:
![]()
где t – наработка до отказа.
2 В случае большой выборки
В этом случае отказы группируются по интервалам. Оценка вероятности безотказной работы вычисляется по формуле:
![]() ,
,
где n(t) - число объектов, безотказно работающих в момент t; N – выборка.
Первое значение t, т.е. t0, принимается равным нулю.
Пример. Оцените вероятность безотказной семисотчасовой работы насоса, если число отказов 100 насосов такого же типа, проработавших столько же часов, равно 40:
Р(700)=60/100=3/5=0,6.
Интенсивность отказов вычисляется:
![]()
где n(t) - число элементов, безотказно работающих в момент t; Δt – ширина интервала.
Выбор закона распределения
Гипотеза распределения принимается по следующей методике:
1 Определяем вид выборки |
||
N < 20 - малая выборка |
N > 20 - большая выборка |
|
2 Строится вариационный ряд наработки: t1 < t2 < t3 < t4 < … <tn. |
2 Общее время наработки до отказа ti разбивается на К интервалов только для большой выборки:
К – число интервалов на практике К=4-12; Δt – ширина интервала; tmax, tmin - максимальное и минимальное значение показателя |
|
3 Для каждого значения Определяются показатели надежности Pi(t), F(t), i(t). Результаты сводятся в таблицу |
3 Для каждого интервала определяются эмпирические характеристики: ni – число отказов в каждом интервале; Р0 – опытная вероятность; i(t) - оценка интенсивности отказов; Pi(t) оценка вероятности безотказной работы в интервале. Результаты сводятся в таблицу |
|
4 Строятся гистограммы Pi(t), F(t), i(t). По виду гистограмм высказывается гипотеза о законе распределения: |
4 Строятся гистограммы Pi(t), i(t). По виду гистограмм высказывается гипотеза о законе распределения: |
|
- если (t) = const, то принимается гипотеза об экспоненциальном законе; - (t) имеет минимум в середине интервала, то принимается нормальный закон распределения; - если (t) убывает или возрастает с увеличением t, то имеет место закон Вейбула-Гнеденко |
||
5 Оценка параметров предполагаемого закона распределения |
||
|
- коэффициент вариации;
|
|
6 Проверка гипотезы о предполагаемом законе распределения: |
||
по критерию Колмогорова |
по критерию Пирсона |
|
Dmax=F*(t) - F(t), где F*(t) – статистическая функция; F(t) – теоретическая функция;
Если Р() 0,5, то гипотеза не противоречит опытным данным. |
Если
χ2
|
|

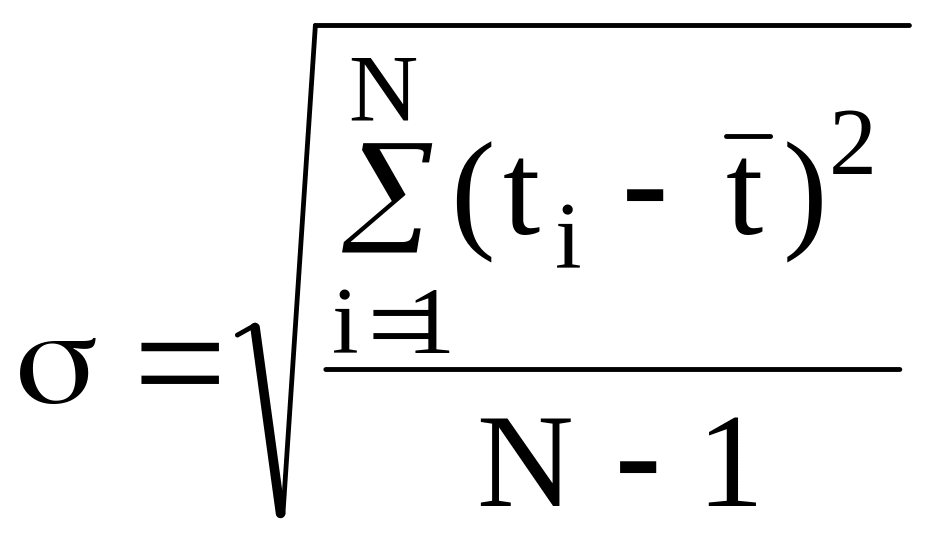 -
среднее квадратическое отклонение
-
среднее квадратическое отклонение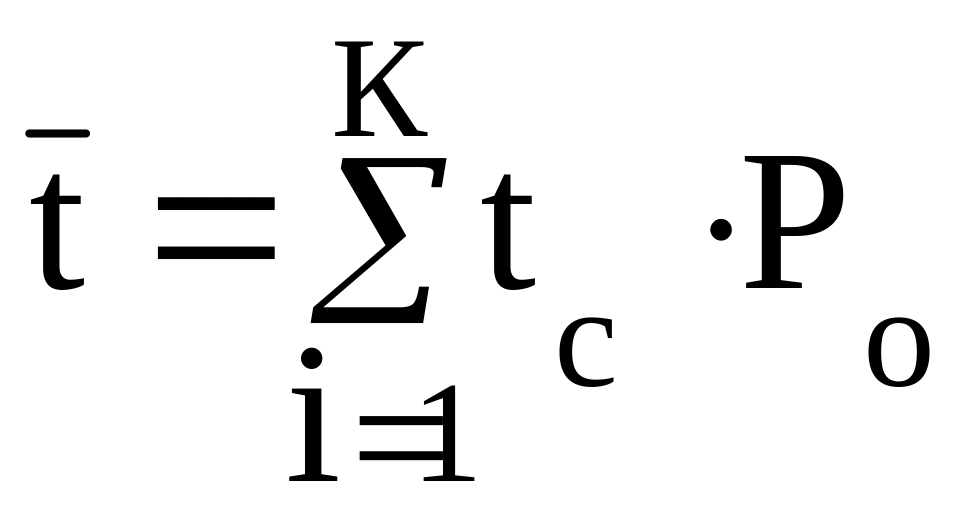 -
среднее арифметическое значение
случайной величины; Ро – опытная
вероятность i-го
интервала;
-
среднее арифметическое значение
случайной величины; Ро – опытная
вероятность i-го
интервала;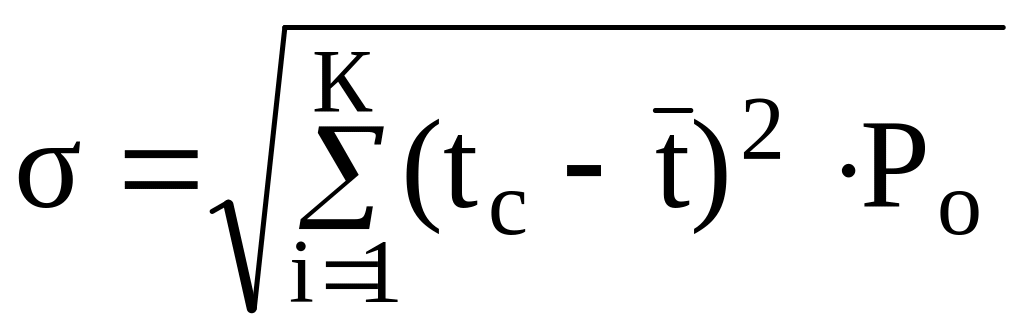 -
среднее квадратическое отклонение
-
среднее квадратическое отклонение