Задачи выбора оптимального числа резервных элементов в системе в случае нагруженного резерва

При параллельном соединении элементов в системе можно создать сложную систему с высоким уровнем надежности из элементов с низкой надежностью.

Но тогда возникает вопрос: сколько же надо поставить резервных элементов, чтобы получить заданную надежность, считая резерв нагруженным?

В простейшем случае задача решается очень быстро. Вспомним выражение для параллельного соединения (в смысле надежности) одинаковых элементов

Р_с(t)= 1 – [1 – Р_э(t)]^х, (6.2)

где х - число необходимых элементов;

Р_с(t) - заданная величина надежности системы;

P_э(t) - надежность элементов.

Решим уравнение (6.2) относительно х, получим:

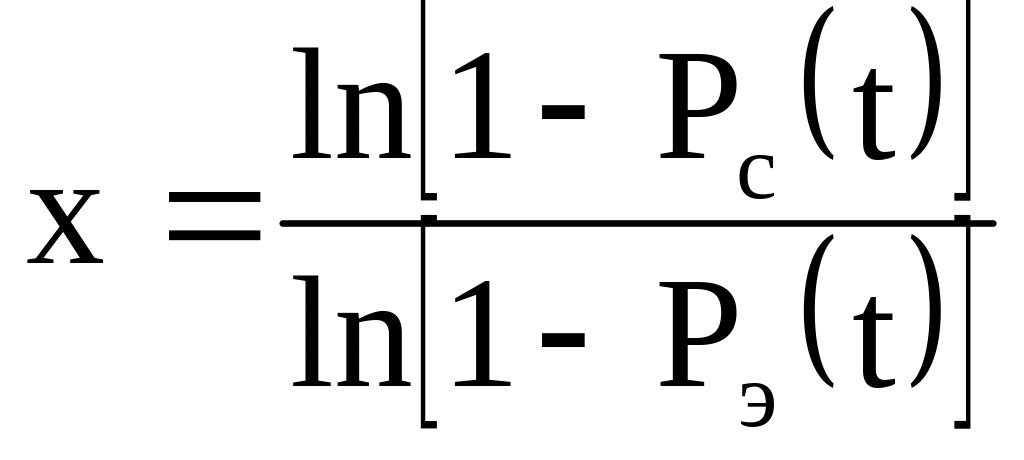. (6.3)

И надо взять целое значение х, округленное в большую сторону.

Пример. Определить необходимое число насосов, которое надо установить в насосной, чтобы показатель надежности функционирования этой станции P_c(t) был бы равен 0,98, в то время как насосы характеризуются показателем P_э(f)=0,8. Считать резерв нагруженным.

Используем выражение (8.3):

.

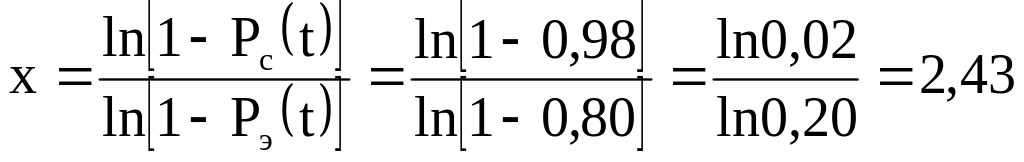Необходимо взять ближайшее большее целое значение х = 3.

Вывод. Таким образом, для достижения заданного уровня надежности надо в насосной иметь три насоса: один основной и два резервных.

Пример. Сравним две схемы с точки зрения надежности (рисунок 6.8).

Пусть для упрощения все элементы обеих схем будут иметь одинаковую надежность (Р₁=Р₂), обозначенную Р.

F₁(t)=(1-P)² F₂(t)=(1-P)² F_1-2(t)=1-P²

P₁(t)=1-(1-P)² P₂(t)=1-(1-P)² P_1-2(t)=1-(1-P²)

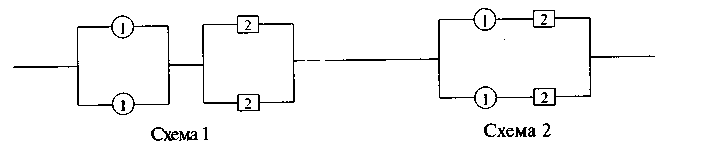
Раздельное резервирование Общее резервирование

(резервируется каждый элемент (резервируется вся система

системы раздельно) 1-2 в общем)

Рисунок 6.8 – Схемы резервирования

Уравнения для надежности систем будут иметь вид:

Р_с1 = [1-(1-P)·(1-P)] · [1-(1-P)·(1-P)] = [1-(1-P)²]²;

Р_с2 = 1-(1-P·P) · (1-P·P)=1-(1-P²)². (6.4)

Упростим выражение (6.4)

Р_с1 = [1-(1-2·P+P²)]² = [Р·(2-P)]² = Р²·(2-P)²;

Р_с2 = 1-(1-2·P²+P⁴) = Р²·(2-P²). (6.5)

Возьмем отношение:

(6.6)

Рассмотрим это отношение в предельных случаях:

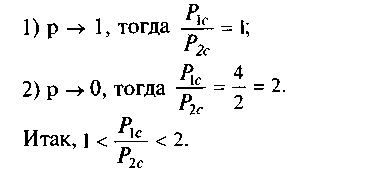
Надо также иметь в виду, что в приведенных примерах мы приняли, что резерв является нагруженным, а в действительности имеет место резерв ненагруженный. А в реальных условиях, конечно, будет функционировать только один компрессор низкого давления и один компрессор высокого давления, резервные будут ожидать своей очереди, либо, находясь в состоянии простоя, либо, находясь в состоянии ремонта, и надежность при этом не будет падать так скоро, как она падает, когда объект находится в нагруженном состоянии.

Расчет надёжности в случае ненагруженного резерва

Пусть система состоит из одного работающего элемента и (N-1) резервных (ненагруженных). Отказ системы наступает в тот момент, когда отказывает последний из N элементов.

Наработка системы до отказа:

t_c = t₁ + t₂ +……+ t_N (6.10)

Пусть все N элементов имеют одинаковое распределение наработки до отказа со средним значением t_o и дисперсией σ².

t_o = (6.11)

Тогда из (6.10) следует:

M(t_c)=N·t₀;

σ²(t_c)= N·σ². (6.12)

При достаточно большом значении t_c (практически при N > 10) вероятность безотказной работы системы с ненагруженным резервом определяется следующим образом

. (6.13)

Пример. Пусть количество элементов с ненагруженным резервом N=9 (1 основной, 8 запасных элементов). Средняя наработка до отказа каждого элемента системы t₀=100 ч. Среднее квадратическое отклонение рассеивания случайной величины σ =50 ч.

Проанализировать изменение вероятности безотказной работы Р_с(t) системы во времени.

Решение.

Определим Р_с(t) по уравнению (6.13). Значение функции F₀(Z) определяем из справочных данных. Результаты сводим в таблицу 8.6.

;

.

Таблица 6.6 - Изменение вероятности безотказной работы системы во времени

t, ч.	600	900	1200
Рс(t)	0,977	0,500	0,023

Такие расчеты важны для определения норм запасных частей.

Из таблицы 8.6 видно, что 8 запасных частей (N=9) хватит на 600 ч. работы с довольно высокой вероятностью Р_с(t)=0,977, а на 900 ч. - только с вероятностью 0,500.

Рассчитаем норму запасных частей для заданной вероятности Р_с(t)=α.

Из формулы (6.13):

.

где - квантиль нормального распределения.

.

Поделим обе части этого уравнения на t₀:

где - средний расход запасных изделий за время t;

- коэффициент вариации.

Тогда:

.

Решим уравнение относительно N:

.

.

. (6.14)

Расчет ненагруженного резерва более сложен, поэтому часто используют схему нагруженного резерва, но надо помнить: это приводит к заниженным значениям надежности.

Однако отметим, что рассмотренные выше методики и решения вполне могут быть использованы при выборе оптимальной схемы, так как если данный вариант имеет лучшую надежность при нагруженном резерве, то в действительности в случае ненагруженного резерва этот вариант тоже будет иметь лучшие показатели.

Лекция 7. Классификация машин и аппаратов по надежности. Работоспособность объекта: анализ области работоспособности.