Структурный анализ систем технологического оборудования

Расчет надежности сложных систем

Надежность системы в целом зависит от надежности входящих в нее элементов, а также от способа их включения в систему.

В теории надежности различают два основных вида соединения элементов: последовательное (рисунок 4.2)и параллельное (рисунок 4.3).

Рисунок 4.1 – Последовательное соединение

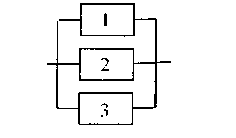
Рисунок 4.3 – Параллельное соединение

Последовательное соединение

Под последовательным соединением элементов в теории надежности понимают такое соединение, при котором отказ одного какого-либо элемента влечет за собой отказ всей системы.

Пример. На рисунке 4.4 приведена схема реактора с герметическим приводом.

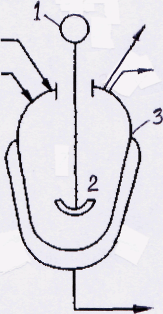
Рисунок 4.4. - Схема реактора с герметическим приводом

Схема надежности реактора будет иметь вид, приведенный на рисунке 4.5.

Р₁ Р₂ Р₃

Рисунок 4.5. - Схема надежности реактора

При рассмотрении схемы (см. рисунок 4.5) легко видеть, что при отказе любого элемента будет иметь место отказ функционирования всей системы.

Тогда, вероятность безотказной работы реактора равна:

(4.1)

Для определения вида соединения необходимо, перечисляя каждый элемент системы друг за другом, задавать вопрос: если этот элемент откажет, то откажет ли вся система? Если система откажет, то данный элемент включен последовательно; если система не откажет, то имеет место другой вид соединения.

На рисунке 4.6 представлены множества Р₁, Р₂, Р₃, представляющие собой функционирование соответствующего элемента по рисунку 4.5, т.е.:

- если вероятность безотказной работы (надежность) привода - это попадание точки в область Р_1;

- вероятность безотказной работы (надежность) перемешивающего устройства - это попадание точки в область Р₂;

- и надежность корпуса – попадание точки в область Р₃,

- то множество работоспособных состояний всей системы Р_с соответствует пересечению множеств Р₁, Р₂, Р₃.

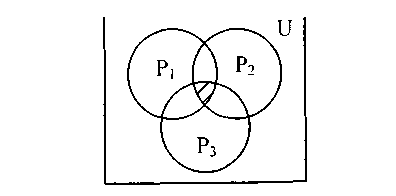
Рисунок 4.6 - Последовательное соединение

Тогда для надежности системы можно записать:

(4.2)

Надежность зависит от времени.

Итак, расчетная формула для определения показателя надежности системы с последовательным соединением элементов:

(4.3)

Из этой формулы можно сделать следующие выводы:

1) Надежность системы с последовательно включенными элементами всегда будет ниже надежности самого ненадежного элемента системы:

2) Чем сложнее система (чем больше элементов в системе) с последовательным соединением элементов, тем ниже ее надежность; при усложнении системы ее надежность будет падать.

В частном случае, если система с последовательным соединением элементов состоит из одинаковых элементов, формула (7.3) приобретает вид:

(4.4)

или

(4.5)

 - интенсивность отказов.

На рисунке 4.7 представлены графики изменения надежности последовательно соединенной системы с одинаковыми элементами в зависимости от числа элементов n при различных значениях показателей надежности P(t) отдельного элемента

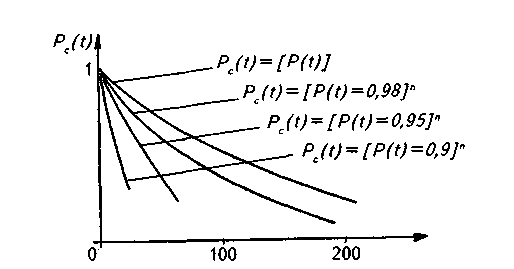t

Рисунок 4.7 - Изменение надежности системы от изменения надежности элемента и числа элементов

Как видно из рисунка 4.7, надежность системы очень сильно зависит от числа элементов в системе.

Параллельное соединение

Системой с параллельным соединением элементов называется такая система, которая отказывает в том случае, если отказали все ее элементы.

Пример такой системы представлен на рис. 7.8.

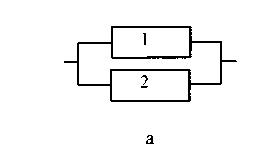
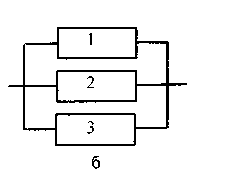
а) б)

Рисунок 4.8 - Системы с параллельным соединением

Случай, изображенный на рисунке 4.8, а, есть дублирование элементов.

На рисунке 4.8, б, система состоит из трех элементов.

Если отказывает любой из трех элементов - система остается работоспособной. Она будет работать и в том случае, если откажут любые два элемента, так как для обеспечения нормального функционирования системы достаточно функционирование всего одного элемента.

Определим надежность функционирования системы на рисунке 4.8, а:

P₁(t) - вероятность безотказной работы первого элемента;

Р₂ (t) - вероятность безотказной работы второго элемента.

Тогда

F₁(t) = 1 – P₁(t) - вероятность отказа первого элемента;

F₂(t) = 1 - Р₂ (t) - вероятность отказа второго элемента.

Вероятность отказа всей системы:

F_с(t) = [1 – P₁(t)] · [1 – P₂(t)]. (4.6)

Вероятность безотказной работы всей системы:

Р_с(t) = 1 - F_с(t) = 1 - [1 – P₁(t)] · [1 – P₂(t)]. (4.7)

В частном случае, если параллельно включенные элементы имеют одинаковую надежность, т.е.:

P₁(t) = P₂(t) = P(t). (4.8)

Будем иметь:

Р_с(t) = 1 - [1 – P₁(t)]². (4.9)

На рисунке 4.9 показана система кругов Р₁, Р₂, Р₃, все точки которых соответствуют работоспособности элементов системы, т.е. любая точка заштрихованного множества объединения отвечает состоянию работоспособности системы

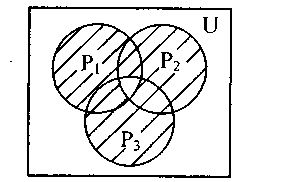
Рисунок 4.9 - Параллельное соединение

Таким образом, расчетная формула для определения показателя надежности системы с параллельным соединением:

Р_с(t) = 1 - [1 – P₁(t)] · [1 – P₂(t)] · ...· [1 – P_n(t)]. (4.10)

Выводы из формулы следующие: