Параметры статистического распределения.

Для проверки гипотез о виде эмпирического закона распределения наибольшее распространение получили критерии Пирсона и Колмогорова.

Критерий Колмагорова

Строим статистическую интегральную функцию распределения F*(t) и теоретическую интегральную функцию распределения F(t) предполагаемого закона.

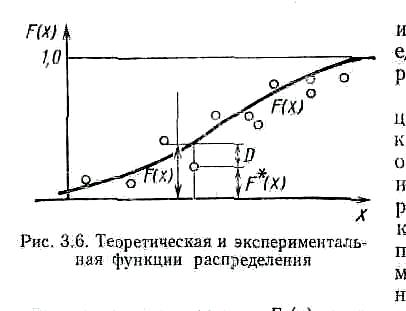
Рисунок 3.2 – Теоретическая и экспериментальная функция распределения

Оцениваем максимальную величину расхождения между функциями:

Dmax=max F*(t) - F(t),

где F*(t) – статистическая функция; F(t) – теоретическая функция;

Определяется условная интенсивность:

.

В зависимости от  находится табличное значение вероятности Р().

Если Р()  0,5, то гипотеза не противоречит опытным данным.

Критерий Пирсона

Требуется определить согласие гипотезы о законе распределения с результатами эксперимента и параметры распределения.

Если , то гипотеза подтверждается.

Доказано, что при n случайная величина х имеет 2 – распределение:

; .

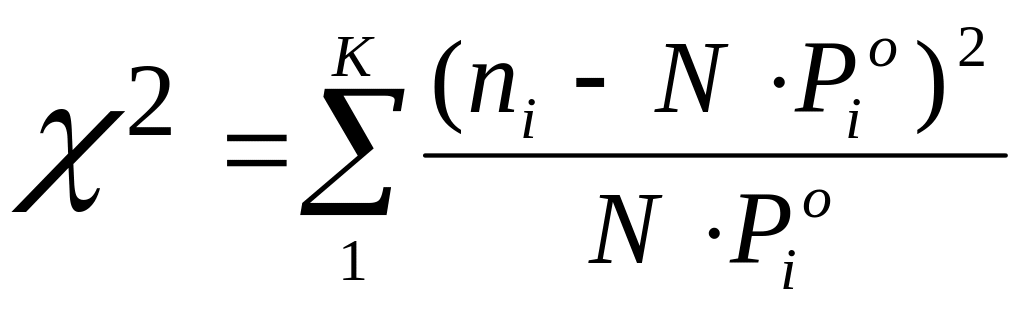
где - табличное значение (выбирается по Р и r); r = K – S + 1 – число степеней свободы; K – число интервалов; S – число обязательных связей: S =2 для нормального закона; S =1 для экспоненциального закона; S = 3 для закона Вейбула.

Лекция 4. Надежность сложных систем. Сложная система и ее характеристики. Структурный анализ систем технологического оборудования

Надежность сложных систем. Сложная система и ее характеристики

Сложная система - объект, который предназначен для выполнения заданных функций и может быть расчленен на элементы, каждый из которых выполняет определенные функции и взаимодействует с другими.

Понятие сложной системы условно. Это понятие может применяться как к отдельным узлам и механизмам, так и машинам в целом и системам машин. Современные нефтеперерабатывающие и нефтехимические машины состоят из тысячи элементов и должны функционировать в течение заданного промежутка времени, не нарушая работоспособности в целом.

Сложная система относительно надежности обладает положительными и отрицательными свойствами:

Отрицательные свойства:

- отказ каждого элемента может привести к отказу системы в целом, так как сложная система имеет большое количество элементов;

- сложные системы во многих случаях являются уникальными или имеются в небольшом количестве, что не позволяет использовать данные для оценки ее работоспособности;

- системы одинакового конструктивного оформления имеют индивидуальные черты. Незначительные изменения свойств отдельных элементов сказываются на выходных параметрах системы. Чем сложнее система, тем больше индивидуальных особенностей она имеет.

Положительные свойства:

- сложным системам свойственно саморегулирование или самоприспособление (находит устойчивое состояние).

- часто для сложной системы возможно восстановление ее работоспособности по частям, не нарушая ее функционирования (дополняется временное отключение отдельных участков для подналадки).

- не все элементы системы одинаково влияют на ее надежность.

Под элементом системы понимается составная часть, которая может характеризоваться самостоятельными входными и выходными параметрами.

Особенности элемента:

- выделяется в зависимости от поставленной задачи (может быть достаточно сложным и состоять из отдельных узлов);

- при исследовании надежности системы элемент не расчленяется на составные части, и показатели безотказности и долговечности относятся к элементу в целом;

- возможно, восстановление работоспособности элемента независимо от других частей и элементов системы.

Пример: Установка АВТ.

Каждый элемент этой установки также представляет собой сложную систему и может быть разбит на отдельные узлы.

Если насос взять как систему, то его элементы: подшипники, система охлаждения, вал, электродвигатель, система смазки и т.д.

При анализе сложных систем их разбивают на подсистемы для последовательного рассмотрения надежности всех составных частей.

Выходные параметры каждого элемента по-разному влияют на формирование выходного параметра всей системы (рисунок 4.1).

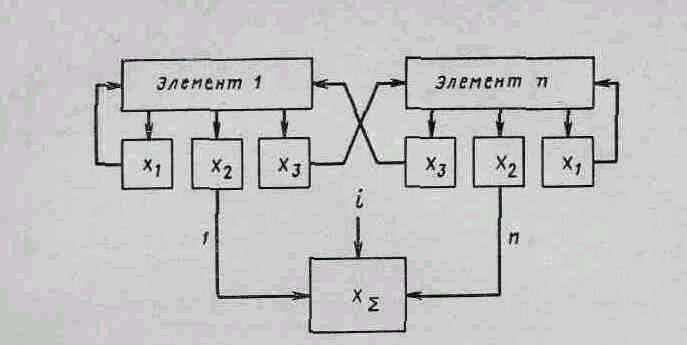
Рисунок 4.1 – Выходные параметры элементов сложной системы

Выделяют три основных свойства этих параметров:

X₁ - изменение параметра влияет на работоспособность только самого элемента. Отказ элемента может привести к отказу системы в целом;

X₂ - параметр участвует в формировании одного или нескольких выходных параметров всей системы;

X₃ - параметр влияет на работоспособность других элементов (его изменения для других элементов аналогично изменению внешних условий, превышения вибрации, повышения температуры).

При анализе сложных систем все элементы делятся на три группы:

- элементы, отказ которых практически не влияет на работоспособность системы (деформация кожуха, изменение окраски поверхности и т. д.);

- элементы с большим запасом прочности;

- элементы, ремонт или резервирование которых возможны во время остановок, которые не влияют на эффективность системы;

- элементы, отказ которых приводит к отказу всей системы.

Необходимое условие безотказной работы - это безотказность работы элементов: