Билет 15. Вероятностное пространство. Предмет теории вероятностей. Предмет теории вероятностей

Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать результат отличает случайное явление от детерминированного.

Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях. Случайность и хаос — не одно и то же. Оказывается, что и в случайных экспериментах наблюдаются некоторые закономерности, например свойство «статистической устойчивости»: если — некоторое событие, могущее произойти или не произойти в результате эксперимента, то доля экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов , приближаясь к некоторому числу . Это число служит объективной характеристикой «степени возможности» событию произойти.

Следует помнить, что мы занимаемся математикой и имеем дело не с реальностью, а лишь с её математической моделью. Мы и будем изучать только математические модели, а приложение их к реальности оставим на долю математической и практической статистики.

Пространство элементарных исходов.

Определение 1. Пространством элементарных исходов («омега») называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой («омега»).

Определение 2. Событиями мы будем называть подмножества множества . Говорят, что в результате эксперимента произошло событие , если в эксперименте произошел один из элементарных исходов, входящих в множество  .

Замечание 2. Вообще говоря, можно назвать событиями не обязательно любые подмножества множества , а лишь элементы некоторого набора подмножеств. О смысле такого ограничения мы поговорим позднее.

Пример 1. Один раз подбрасывается кубик — игральная кость. Рассмотрим пространство элементарных исходов , элементарные исходы здесь соответствуют числу выпавших очков.

Примеры событий: — выпало одно или два очка; — выпало нечётное число очков.

Пример 4. Монета подбрасывается до тех пор, пока не выпадет вверх гербом. Пространство элементарных исходов состоит из бесконечного, но счётного числа исходов: , где  р  означает выпадение решки, а  г  — герба при одном подбрасывании.

Билет 16. Теоремы сложения вероятностей

Несколько событий называются несовместимыми, если появление одного из них исключает возможность появления остальных.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий

P (AÈB) =P (A) +P (B). (2.1)

Если имеется счетное множество несовместных событий A₁, ... , A_n, то

. (2.2)

Из правила сложения вероятностей вытекает, что если события A₁, A₂, …, A_n несовместны и образуют полную группу, то сумма их вероятностей равна единице; т.е. если

A_iּA_j=О при i≠j, то

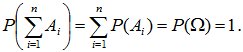(2.3)

В частности, если два события А и противоположны, то они образуют полную группу несовместных событий и

(2.4)

Тогда

(2.5)

Вероятность суммы двух совместных событий равна сумме вероятностей каждого из событий минус вероятность их совместного появления:

. ошибка-пересечение (2.6)

Билет 17. Условные вероятности. Независимость событий

словная вероятность события A при выполнении события B обозначается P(A|B). Условной вероятностью события A при выполнении события B называется отношение P(A|B) = Здесь предполагается, что P(B)>0. В качестве разумного обоснования этого определения отметим, что при наступлении события B оно начинает играть роль достоверного события, поэтому надо потребовать, чтобы P(В|B) =1. Роль события A играет AB, поэтому P(A|B) должна быть пропорциональна P(АB). (Из определения следует, что коэффициент пропорциональности равен 1/P(В))

Независимость событий

События A и B называются независимыми, если P(A|B)=P(A). Это означает: оттого, что произошло событие B, вероятность события A не изменилась. С учетом определения условной вероятности, это определение сведется к следующему соотношению P(AB) = P(A)P(B). В этом соотношении нет необходимости требовать выполнения условия P(B)>0.Таким образом, приходим к окончательному определению. События A и B называются независимыми, если P (AB) = P(A)P(B). Последнее соотношение обычно и принимают за определение независимости двух событий. Несколько событий называются независимыми в совокупности, если подобные соотношения выполняются для любого подмножества рассматриваемых событий. Так, например, события A,B,C, независимы в совокупности, если выполняются соотношения P(ABC)=P(A)P(B)P(C), P(AB)=P(A)P(B), P(AC)=P(A)P(C), P(CB)=P(C)P(B). ^

Задачи на условную вероятность и независимость событий

Задача 21.. Из полной колоды из 36 карт вытаскивают одну карту. Событие A - карта красная, B – карта туз. Будут ли они независимы? Решение. Согласно классическому определению вероятности P(B)= 1/9 P(A)=1/2, P(AB)=1/18. Это означает, что события A и B .независимы. Задача 22. Решить ту же задачу для колоды, из которой удалена дама пик. Решение. P(A)=18/35, P(B)=4/35, P(AB)=2/35. Независимости нет. Задача 23. Двое поочередно бросают монету. Выигрывает тот, у которого первым выпадет герб. Найти вероятности выигрыша для обоих игроков. Решение. Можно считать, что элементарные события – это конечные последовательности вида (0,0,1,…,0,1). Для последовательности длины n соответствующее элементарное событие имеет вероятность Игрок, начинающий бросать монету первым, выигрывает, если реализуется элементарное событие , состоящее из нечетного числа нулей и единиц. Поэтому вероятность его выигрыша равна 1/2 + 1/8+1/32 + ….= Выигрыш второго игрока соответствует четному числу нулей и единиц. Он равен 1/4+1/16 +1/64+…..= Из решения следует, что игра заканчивается за конечное время с вероятностью 1.(т.к. 1/3+2/3=1). Задача 24. Для того чтобы разрушить мост, нужно попадание не менее 2 бомб. Сбросили 3 бомбы с вероятностями попадания 0.1, 0.3, 0.4. Найти вероятность разрушения моста. Решение. Пусть события A,B,C состоят в попадании 1,2,3 бомбы соответственно. Тогда разрушение моста соответствует событию В силу того, что слагаемые в этой формуле попарно несовместны, а сомножители в слагаемых независимы, искомая вероятность равна (0.1)(0.3)(0.4)+ (0.1)(0.3)(0.6)+ (0.1)(0.7)(0.4)+ (0.9)(0.3)(0.4)=0.166.