13. Механическая работа — физическая величина, зависящая от векторов силы и перемещения. Работа силы (сил) над одной точкой[править | править исходный текст]

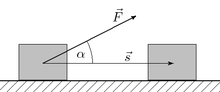
• Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4],   — вектор перемещения; подразумевается, что действующая сила   постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений   если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

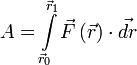где   и   — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

14.

Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени^[1].

Различают среднюю мощность за промежуток времени 

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

15. В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом^[2]

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.

16. Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

• все тела состоят из частиц: атомов, молекул и ионов;

• частицы находятся в непрерывном хаотическом движении (тепловом);

• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.

МКТ стала одной из самых успешных физических теорий и была подтверждена целым рядом опытных фактов. Основными доказательствами положений МКТ стали:

• Диффузия

• Броуновское движение

• Изменение агрегатных состояний вещества

На основе МКТ развит целый ряд разделов современной физики, в частности, физическая кинетика и статистическая механика. В этих разделах физики изучаются не только молекулярные (атомные или ионные) системы, находящиеся не только в «тепловом» движении, и взаимодействующие не только через абсолютно упругие столкновения. Термин же молекулярно-кинетическая теория в современной теоретической физике уже практически не используется, хотя он встречается в учебниках по курсу общей физики.

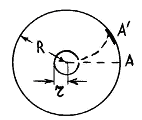
17. В 1920 г. О. Штерн разработал метод атомных (молекулярных) пучков и с его помощью экспериментально измерил скорость теплового движения молекул газа, а также проверил распределение Максвелла. Установка Штерна состояла из двух коаксикальных цилиндров, на оси которых находилась платиновая проволока, покрытая слоем серебра. (рис. 1). В приборе создавался высокий вакуум. При пропускании по проволоке тока она раскалялась и с ее поверхности испарялись атомы серебра, которые вылетали через узкую щель, проделанную во внутреннем цилиндре, и достигали стенки наружного цилиндра (в точке A на рис. 1).

рис. 1

В результате образовывалась узкая серебряная полоска, являющаяся изображением щели. Затем весь прибор приводился во вращение вокруг оси цилиндров с постоянной угловой скоростью  , при этом полоска смещалась в сторону противоположную вращению на величину  =AA'. Смещение возникало, потому что за время t пролета атомом серебра расстояния R-r цилиндр успевал повернуться на угол   =  /R =  t. Откуда определялось время t =  / R, знание которого позволяло найти скорость атома серебра через измеримые параметры опыта:

Как следовало ожидать, полоска серебра в положении А' оказывалась размытой из-за того, что атомы серебра имеют разные скорости: более быстрым атомам соответствуют меньшие, а более медленным – большие смещения  . Исследуя зависимость плотности серебра в размытой части от расстояния до точки A, нетрудно оценить распределение атомов серебра по скоростям. Полученное распределение хорошо согласовывалось со значениями, вычисленными по формуле   .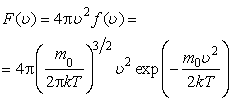

Более совершенный метод по проверке закона Максвелла был реализован в 1929 г. Ламертом. В высоком вакууме вращаются, насаженные на общую ось, два круглых диска 1 и 2 с радиальными узкими прорезями (рис. 2), смещенными друг относительно друга на угол  . Напротив прорези диска 1 находилась тигельная печь 3 с исследуемым веществом и диафрагма 4. Вся установка приводилась во вращение с постоянной угловой скоростью. Очевидно, атомы, вылетевшие со скоростью v из печи, достигают мишени 5, если время их пролета расстояния между дисками t₁ = l/v совпадает со временем t₂ поворота диска 2 на угол  , т.е. t₂ =  / . Из условия t₁ = t₂ находим v = l / . Меняя угловую скорость вращения  , можно выделить атомы с различными скоростями. Улавливая атомы, движущиеся с различными скоростями в течение равных промежутков времени, можно по толщине (плотности) осадка на мишени определить их относительное количество в пучке и тем самым проверить закон распределения Максвелла. Обработка экспериментальных результатов, полученных на установке Ламерта, показала полное согласие их с законом Максвелла.

рис. 2

18. Идеальный газ — математическая модель газа, в которой предполагается, что: 1) потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объем молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют также форму в виде упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц и др.^[1].

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).