3.2.Правила дифференцирования

1. Производная постоянной равна нулю: с¢=0.

2. Если функция u и v дифференцируемы в точке x_0, то их сумма или разность дифференцируемы в этой же точке x₀:

.

3. Если функции u и v дифференцируемы в точке x₀, то их произведение дифференцируемо в этой же точке, причем:

.

3. Если функция u и v дифференцируемы в данной точке и функция v не равна нулю, то производная дроби также является дифференцируемой в этой точке и ее производная находится по формуле:

3. Постоянный множитель выносится за знак производной. В частности, если функция u дифференцируема в точке x₀ и c – постоянная, то

и .

Производная сложной функции.

Если функция u=φ(x) дифференцируема в точке x₀, а функция дифференцируема в точке , то сложная функция дифференцируема в точке x₀ и

или .

Производная обратной функции.

Для дифференциальной функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции

.

3.3. Основные формулы дифференцирования

Если y – сложная функция от x, т.е. 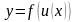, где x – независимая переменная, то имеют место следующие формулы (табл. 1).

Таблица 1

Основные формулы нахождения производной функции

	Производные простых функций	Производные сложных функций
1.	, n¹ 1	, где n=Соnst
2.	, где a>0, a¹1	, где a>0, a¹1
3.	, где a>0, a¹1	, где a>0, a¹1
4.
5.
6.
7.
8.
9.
10.
11.

Пример 3.1. Найти производную функции: .

Решение:

Воспользуемся формулами: ; c¢=0; .

y¢= ((5x²– 4x +10)⁷)¢ = 7(5x²– 4x +10) (5x²–4x +10)¢ =

=7(5x²– 4x +10) (5×2x^2–1– 4×( ) x + 0) =

=7(5x² – 4x +10) (10 x – x )=7(5x² – 4 +10)⁶ (10x + ).

Пример 3.2. Найти производную функции: y = ln(5x–1).

Решение:

Для решения используем формулы: (ln u) u; (u±v) u ± v; с =0.

y= ln(5x–1))= = = (5–0)=

= 5= .

Пример 3.3. Найти производную функции: y = ln

Решение:

Преобразуем логарифмическую функцию, воспользовавшись свойствами логарифма:

ln = ln a – ln b ; ln a =nln a.

y=ln =ln( ) = ln( )= (ln(7x+2) – ln(3x–7)) =

= ln(7x+2)– ln(3x–7).

Дифференцируем:

y=( =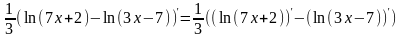

=

= .

Для нахождения производных применены следующие формулы:

(ln u)= ; (u ± v)u ± v, с = 0,(сu)′=cu′.

Пример 3.4: Найти производную функции: у = arccos 3x.

Решение:

Воспользуемся формулой: (arccos u) .

y .

Пример 3.5: Найти производную функции: y = cos3x.

Решение:

y= (cos3x)=–sin3x(3x)=–3sin 3x.

Использованы формулы: (cosu)=–sinu∙u′, (cu)′=cu′, x′=1, c′=0.

Пример 3.6: Найти производную функции: _.

Решение:

Используем формулы: .

.

Пример 3.7: Найти производную функции: y=5^sinx.

Решение:

Применяем соотношения: _.

.

Пример 3.8. Найти производную функции:

Решение:

Так как исходное выражение представляет собой произведение двух функций, то его производная находится по формулам:

(uv)′ = u′v + uv′ и

Пример 3.9. Найти производную функции:

Решение:

При решении используем: .

Пример 3.10. Найти производную функции: y=arcsin

Решение:

Для нахождения производной применяем формулы: