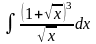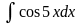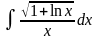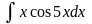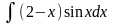- •Балаш о.С., Высочанская е.Ю., Попова а.А., Коробченко е.В. Математика
- •Балаш о.С., Высочанская е.Ю., Попова а.А., Коробченко е.В. Математика
- •Оглавление
- •Введение
- •1. Аналитическая геометрия
- •1.1 Расстояние между двумя точками
- •1.2. Середина отрезка
- •1.3. Уравнение прямой на плоскости
- •1.3.1.Общее уравнение прямой на плоскости
- •1.3.2.Уравнение прямой с угловым коэффициентом
- •1.3.3.Уравнение прямой в отрезках
- •1.3.4.Уравнение прямой, проходящей через данную точку в данном направлении
- •1.3.5.Уравнение прямой, проходящей через две заданные точки
- •1.4. Угол между прямыми
- •1.5. Пересечение двух прямых
- •1.6. Расстояние от точки до прямой
- •1.7. Задания для самостоятельной работы
- •Пределы и непрерывность
- •2.1. Основные теоремы о пределах
- •2.2. Замечательные пределы
- •2.3. Непрерывность функции
- •2.4. Задания для самостоятельной работы
- •3. Дифференциальное исчисление функции одной переменной
- •3.1. Понятие производной
- •3.2.Правила дифференцирования
- •3.3. Основные формулы дифференцирования
- •3.4. Применение дифференциального исчисления для исследования функции
- •3.4.1. Монотонность функции
- •3.4.2. Экстремум функции
- •Интервалы возрастания и убывания функции
- •3.4.3. Выпуклость и вогнутость кривой. Точки перегиба
- •3.4.4. Асимптоты кривых
- •3.4.5. Исследование функции и построение графиков
- •3.5. Задания для самостоятельной работы
- •4. Интегральное исчисление
- •4.1. Первообразная функция и неопределенный интеграл
- •4.2. Основные свойства неопределенного интеграла.
- •4.3. Таблица простейших неопределенных интегралов
- •4.4. Основные методы интегрирования
- •4.4.1. Непосредственное интегрирование
- •4.4.2. Метод подстановки (метод замены переменной)
- •4.4.3. Метод интегрирования по частям
- •4.4.4. Интегрирование рациональных дробей. Метод неопределенных коэффициентов
- •Определенный интеграл
- •Геометрическое приложение определенных интегралов
- •Задания для самостоятельной работы
- •5. Дифференциальные уравнения
- •5.1. Дифференциальные уравнения первого порядка
- •5.1.1.Дифференциальные уравнения с разделяющимися переменными
- •5.1.2.Однородные дифференциальные уравнения
- •5.1.3.Линейные дифференциальные уравнения первого порядка
- •5.2. Дифференциальные уравнения второго порядка
- •Вид частных решений неоднородного дифференциального уравнения с постоянными коэффициентами
- •Задания для самостоятельной работы
- •Список литературы Основная литература
- •Дополнительная литература
- •Математика
- •410052, Саратов, ул. Международная, 24
- •410052, Саратов, ул. Международная, 24
Определенный интеграл
Пусть
функция f(x)
определена на отрезке [a; b],
где a<b.
Разобьем отрезок на n
произвольных частей точками a=х0<
х1<…<
хi–1<
хi
<…< хn–1<
хn=b.
На каждом отрезке [хi–1; хi]
выберем произвольную точку
 и положим
и положим
 ,
где i
=1,…n.
Значение функции
,
где i
=1,…n.
Значение функции
 умножим на длину отрезка
умножим на длину отрезка
 и составим сумму всех таких произведений.
и составим сумму всех таких произведений.
Сумма
вида
 называется
интегральной суммой
для функции f(x)
на отрезке [a; b].
Геометрически
интегральная сумма представляет собой
алгебраическую сумму площадей
прямоугольников, в основании которых
лежат частичные отрезки
,
а высоты равны
.
называется
интегральной суммой
для функции f(x)
на отрезке [a; b].
Геометрически
интегральная сумма представляет собой
алгебраическую сумму площадей
прямоугольников, в основании которых
лежат частичные отрезки
,
а высоты равны
.
Обозначим
через
 максимальную длину частичного отрезка
разбиения. Найдем предел интегральной
суммы при условии, что длина наибольшего
частичного отрезка стремится к нулю,
т.е.
максимальную длину частичного отрезка
разбиения. Найдем предел интегральной
суммы при условии, что длина наибольшего
частичного отрезка стремится к нулю,
т.е.
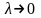 .
.
Под
определенным
интегралом
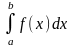 от данной непрерывной функции f(x)
на данном отрезке [a; b]
понимается предел интегральных сумм
при
от данной непрерывной функции f(x)
на данном отрезке [a; b]
понимается предел интегральных сумм
при
 ,
то есть:
,
то есть:
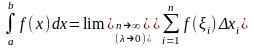 .
(4.8)
.
(4.8)
Числа a и b называются нижним и верхним пределами интегрирования соответственно, а отрезок [a,b] – областью (отрезком) интегрирования.
Если функция f(x) непрерывна на отрезке [a; b] и функция F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона–Лейбница:
 .
(4.9)
.
(4.9)
Пример
4.10.
Вычислить:
 .
.
Решение:
Найдем первообразную от степенной функции, а затем воспользуемся формулой Ньютона – Лейбница (4.9):
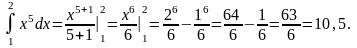
Пример
4.11.
Вычислить:
 .
.
Решение:


Геометрическое приложение определенных интегралов
Формулировка определенного интеграла позволяет получить различные формулы для нахождения длин, площадей и объемов геометрических фигур.
Площадь криволинейной трапеции, ограниченной линиями y1(x) y2(x), х=а, х=b, вычисляется по формуле:
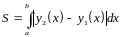 ,
(4.10)
,
(4.10)
где а; b – абсциссы точек пересечения кривых y1 (x) и y2 (x).
Пример
4.12: Найти
площадь фигуры, образованной параболой
 и прямой
и прямой
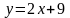 .
Сделать чертеж.
.
Сделать чертеж.
Решение:
Выполним чертеж.
Построим прямую по точкам A(0; 9) и B(–4,5; 0).
Для
построения и анализа параболы y(x)=x2+6x+9
приведем ее к каноническому виду:
 .
.
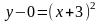 – это
парабола с вершиной в точке: (–3; 0) с осью
симметрии параллельной оси Ох и ветвями,
направленными вверх.
– это
парабола с вершиной в точке: (–3; 0) с осью
симметрии параллельной оси Ох и ветвями,
направленными вверх.
Точка пересечения параболы с осью Оy : C(0; 9) с осью Ох: D( –3; 0).
Найдем а и b – точки пересечения параболы и прямой. Для этого решим систему уравнений:

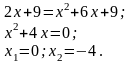
Таким образом, а= –4; b=0. Построим чертеж:
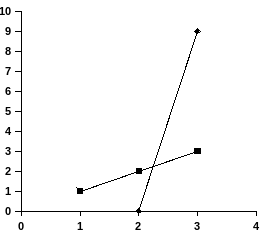
Найдем площадь фигуры по формуле (4.10):
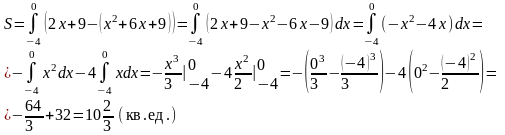
Задания для самостоятельной работы
Найти интегралы.
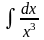 (Ответ:
(Ответ:
 .)
.) (Ответ:
(Ответ:
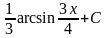 .)
.)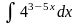 (Ответ:
(Ответ:
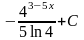 .)
.)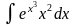 (Ответ:
(Ответ:
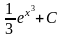 .)
.) (Ответ:
(Ответ:
 .)
.)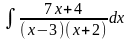 (Ответ:
(Ответ:
 .)
.)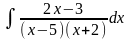 (Ответ:
(Ответ:
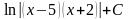 .)
.)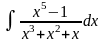 (Ответ:
(Ответ:
 .)
.)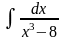 (Ответ:
(Ответ:
 .)
.)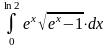 (Ответ:
(Ответ:
 .)
.)Найти площадь фигуры, образованной линиями
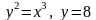 и х=0.
(Ответ:
и х=0.
(Ответ:
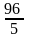 )
)Найти площадь фигуры, образованной кривыми
 и
и
 .
.
(Ответ:
 )
)
Вычислить интегралы, используя непосредственное интегрирование:
Вычислить интегралы, используя метод замены переменной:
Вычислить интегралы, используя метод интегрирования по частям:
|
|
|
|
|
|
|
|
|
|
|
|