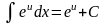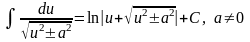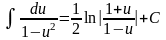- •Балаш о.С., Высочанская е.Ю., Попова а.А., Коробченко е.В. Математика
- •Балаш о.С., Высочанская е.Ю., Попова а.А., Коробченко е.В. Математика
- •Оглавление
- •Введение
- •1. Аналитическая геометрия
- •1.1 Расстояние между двумя точками
- •1.2. Середина отрезка
- •1.3. Уравнение прямой на плоскости
- •1.3.1.Общее уравнение прямой на плоскости
- •1.3.2.Уравнение прямой с угловым коэффициентом
- •1.3.3.Уравнение прямой в отрезках
- •1.3.4.Уравнение прямой, проходящей через данную точку в данном направлении
- •1.3.5.Уравнение прямой, проходящей через две заданные точки
- •1.4. Угол между прямыми
- •1.5. Пересечение двух прямых
- •1.6. Расстояние от точки до прямой
- •1.7. Задания для самостоятельной работы
- •Пределы и непрерывность
- •2.1. Основные теоремы о пределах
- •2.2. Замечательные пределы
- •2.3. Непрерывность функции
- •2.4. Задания для самостоятельной работы
- •3. Дифференциальное исчисление функции одной переменной
- •3.1. Понятие производной
- •3.2.Правила дифференцирования
- •3.3. Основные формулы дифференцирования
- •3.4. Применение дифференциального исчисления для исследования функции
- •3.4.1. Монотонность функции
- •3.4.2. Экстремум функции
- •Интервалы возрастания и убывания функции
- •3.4.3. Выпуклость и вогнутость кривой. Точки перегиба
- •3.4.4. Асимптоты кривых
- •3.4.5. Исследование функции и построение графиков
- •3.5. Задания для самостоятельной работы
- •4. Интегральное исчисление
- •4.1. Первообразная функция и неопределенный интеграл
- •4.2. Основные свойства неопределенного интеграла.
- •4.3. Таблица простейших неопределенных интегралов
- •4.4. Основные методы интегрирования
- •4.4.1. Непосредственное интегрирование
- •4.4.2. Метод подстановки (метод замены переменной)
- •4.4.3. Метод интегрирования по частям
- •4.4.4. Интегрирование рациональных дробей. Метод неопределенных коэффициентов
- •Определенный интеграл
- •Геометрическое приложение определенных интегралов
- •Задания для самостоятельной работы
- •5. Дифференциальные уравнения
- •5.1. Дифференциальные уравнения первого порядка
- •5.1.1.Дифференциальные уравнения с разделяющимися переменными
- •5.1.2.Однородные дифференциальные уравнения
- •5.1.3.Линейные дифференциальные уравнения первого порядка
- •5.2. Дифференциальные уравнения второго порядка
- •Вид частных решений неоднородного дифференциального уравнения с постоянными коэффициентами
- •Задания для самостоятельной работы
- •Список литературы Основная литература
- •Дополнительная литература
- •Математика
- •410052, Саратов, ул. Международная, 24
- •410052, Саратов, ул. Международная, 24
3.5. Задания для самостоятельной работы
Найти производные функций:







Исследовать функции и построить их графики.
y = x2 +x


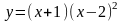


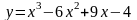
4. Интегральное исчисление
4.1. Первообразная функция и неопределенный интеграл
Функция F(x) называется первообразной функции f(x) на промежутке Х, если для всех х из этого промежутка выполняется равенство F (x)= f(x).
Совокупность
всех первообразных для функций f(x)
называется неопределенным
интегралом
от функции f(x)
и обозначается
 :
:
 .
(4.1)
.
(4.1)
Функция f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования, а С – произвольной постоянной.
Операция нахождения неопределенного интеграла называется интегрированием.
4.2. Основные свойства неопределенного интеграла.
Производная от неопределенного интеграла равна подынтегральной функции, т.е.

Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

Постоянный множитель можно выносить за знак неопределенного интеграла, т.е.
 ,
где а=
Сonst.
,
где а=
Сonst.
Интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от этих функций, т.е.
 .
.
Если
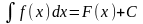 ,
то если вместо переменной х
подынтегральной функции f(х)
и первообразной
F(х)
подставить выражение (kх+b),
тогда
появляется дополнительный множитель
перед первообразной, т.е.
,
то если вместо переменной х
подынтегральной функции f(х)
и первообразной
F(х)
подставить выражение (kх+b),
тогда
появляется дополнительный множитель
перед первообразной, т.е.
 ,
где k
и
b
– некоторые числа, k≠0.
,
где k
и
b
– некоторые числа, k≠0.
Если x – независимая переменная и
 ,
то неопределенный интеграл не зависит
от выбора аргумента, т.е.
,
то неопределенный интеграл не зависит
от выбора аргумента, т.е.
 ,
где u(x)
–
непрерывно дифференцируемая функция
от независимой переменной x.
,
где u(x)
–
непрерывно дифференцируемая функция
от независимой переменной x.
4.3. Таблица простейших неопределенных интегралов
В таблице интегралов, переменная х формально замена на u, которая может обозначать как независимую переменную, так и функцию от независимой переменной, т.к. неопределенный интеграл не зависит от выбора аргумента.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4. Основные методы интегрирования
При вычислении интеграла необходимо, пользуясь теми или иными приемами интегрирования, привести его к табличному и, таким образом, найти искомый результат. Наиболее важными методами интегрирования являются:
непосредственное интегрирование;
метод подстановки (метод замены переменной);
метод интегрирования по частям.