3 Дәріс. Векторлармен жұмыс, оларға қолданылатын функциялар
Matlab-та басқа жүйелер сияқты а…z латын алфавиті мен 0….9 сандары қолданылады.
Matlab−та арифметикалық операторлар саны айтарлықтай көп және матрицалық және арифметикалық операциялардан тұрады. 6−кестеде арифметикалық операторлардың тізімі көрсетілген.
6− кесте
-
Функция
Белгіленуі
Синтаксисі
Қосу
+
(М1+М2)
Азайту
-
(М1-М2)
Матрицалық көбейту
*
(М1*М2)
Элемент бойынша массивтерді көбейту
.*
(М1.*М2)
Матрицаны солдан оңға қарай бөлу
/
(М1/М2)
Элемент бойынша матрицаны солдан оңға қарай бөлу
./
(М1./М2)
Матрицаны оңнан солға қарай бөлу
\
(М1\М2)
Элемент бойынша матрицаны оңнан солға қарай бөлу
.\
(М1.\М2)
MatLab-та логикалық операторлар арифметикалық операторларға қарағанда бірінші орындалады, дәрежелеу көбейту және бөлуге қарағанда басымырақ, ал бөлу мен көбейту қосу мен алуға қарағанда басымырақ, операциялар приоритетiн жоғарылату үшiн дөңгелек жақша қолданылуы керек. Жақшалардың саны шектелмейдi.
Ал, енді векторларды енгізуге келетін болсақ, командалар қатарында вектор атын көрсетіп, сосын = белгісін қоямыз да, квадратты жақшаны ашып, ішіне вектор элементтерін пробел немесе , таңбасы арқылы енгіземіз, сосын квадратты жақшаны жабамыз. Нәтиже жол түрінде шығады, ал егер элементтердің арасына ; таңбасын қойсақ нәтиже баған түрінде шығады. Мысалы, 3.1 суретке қарайық:
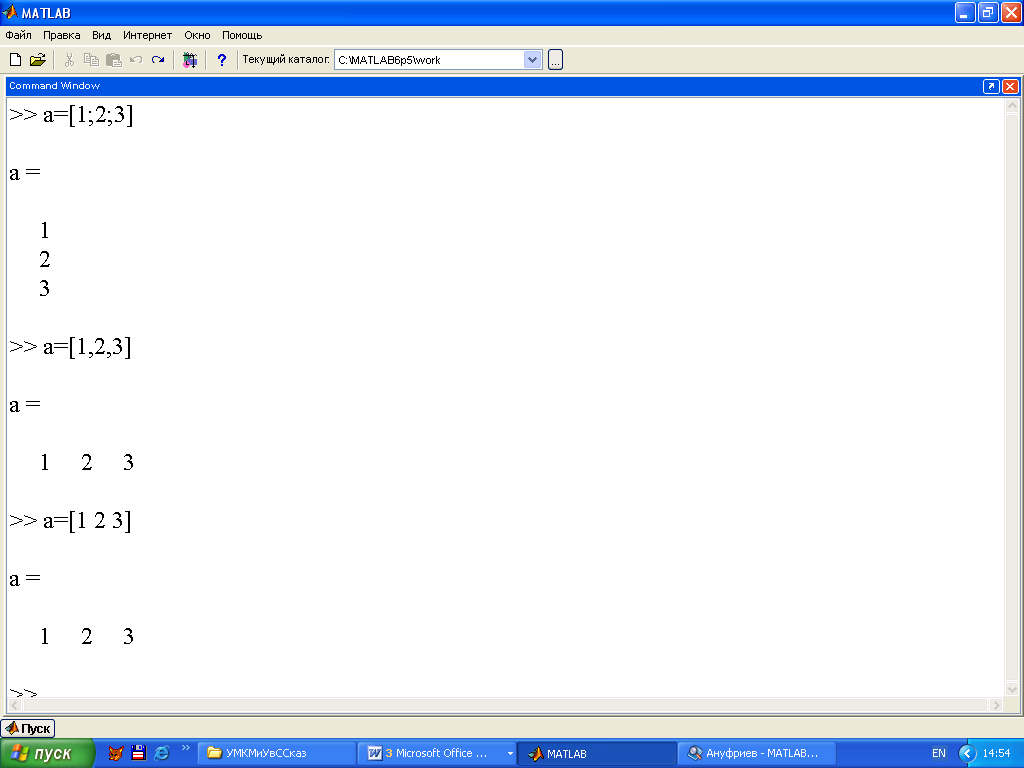
3.1 Сурет. Векторды енгізу
MatLab-та векторларға және матрицаларға қолданылатын бірнеше функциялар бар, солармен танысайық:
>> v=[1 2 3 4 5];
>> prod(v)
ans =
120
prod(v) - % v векторының элементтерінің көбейтіндісі
>> v=[-1 0 -3 9 5];
>> p=mean(v) % арифметикалық ортасы
p=
2
>> v=[-1 0 -3 9 5];
>> p=sort(v) % өсу ретімен орналастыру
p=
-3 -1 0 5 9
>> v=[-1 0 -3 9 5];
>> p= -sort(-v) % кему ретімен орналастыру
p=
9 5 0 -1 -3
>> a=[1 2 3; 7 9 5]
а=
1 2 3
7 9 5
>> prod(a,1) % а матрицасының элементтерін баған бойынша көбейту
ans =
7 18 15
>> prod(a,2) % а матрицасының элементтерін жол бойынша көбейту
ans =
6
315
>> sum(v) % v векторының элементтерінің қосындысы
ans =
15
>> sum(a,1) % а матрицасының элементтерінің баған бойынша қосындысы
ans =
8 11 8
>> sum(a,2) % а матрицасының элементтерінің жол бойынша қосындысы
ans =
6
21
>> a=[1 -1 3; -1 2 0; 3 -2 1]
a =
1 -1 3
-1 2 0
3 -2 1
>> b=2*a % а матрицасының әр элементі 2-ге көбейтіледі
b =
2 -2 6
-2 4 0
6 -4 2
>> a/3+2*(b-a)
ans =
2.3333 -2.3333 7.0000
-2.3333 4.6667 0
7.0000 -4.6667 2.3333
>> a' % а матрицасын транспонирлеу
ans =
1 -1 3
-1 2 -2
3 0 1
>> a*b % а және b матрицасының көбейтіндісі
ans =
22 -18 12
-6 10 -6
16 -18 20
>> v=[1 2 3 4 7];
>> length(v) % v векторының жолының ұзындығы
ans =
5
>> v1=[1.2; 0.3; -1.1];
>> v2=[-0.9; 2.1; 0.5];
>> dot(v1,v2) % екі векторды скалярлық көбейту
ans =
-1
>> sum(v1.*v2) % скалярлық көбейту
ans =
-1
>> cross(v1,v2) % екі векторды векторлық көбейту
ans =
2.4600
0.3900
2.7900
>> v1=[1.2; 0.3; -1.1];
>> min(v1) % v1 векторының min элементін табу
ans =
-1.1000
>> [k,n]=min(v1) % v1 векторының min элементін табу және оның орнын көрсету
k =
-1.1000
n =
3
>> M=[1 2 3; -2 4 7; 6 -3 9]
M =
1 2 3
-2 4 7
6 -3 9
>> det(M) % матрицаның анықтауышы
ans =
123
>> rank(M) % матрицаның рангы
ans =
3
>> M=[5 7 6 5; 7 10 8 7; 6 8 10 9; 5 7 9 10];
>> norm(M) % матрицаның нормасы
ans =
30.2887
>> cond(M)
ans =
2.9841e+003
>> eye(3.3) % 3х3өлшемді матрицаның бас диагональ элементтерін 1-ге айналдырады
ans =
1 0 0
0 1 0
0 0 1
>> ones(3,3) % бірлік матрица
ans =
1 1 1
1 1 1
1 1 1
>> zeros(3,3) % нольдік матрица
ans =
0 0 0
0 0 0
0 0 0
>> rand(3,3) % 0 мен 1 аралығында кездесетін кез келген сандардан құралаған матрица
ans =
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
>> hadamard(4) % Адамар матрицасы
ans =
1 1 1 1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 1
>> a=[1 2 3; 4 5 6; 7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> fliplr(a) % матрицаның сол жағын оң жағымен ауыстыру
ans =
3 2 1
6 5 4
9 8 7
>> flipud(a) % матрицаның асты мен үстін ауыстыру
ans =
7 8 9
4 5 6
1 2 3
>> rot90(a) % матрицаны 90°-қа өзгерту
ans =
3 6 9
2 5 8
1 4 7
>> m=3; n=3;
>> reshape(a,m,n) *а матрицасын қайта қалпына келтіру*
ans =
1 2 3
4 5 6
7 8 9
>> tril(a) % бас диагональдан жоғары элементтерді нөлге айналдырады
ans =
1 0 0
4 5 0
7 8 9
>> triu(a) % бас диагональдан төменгі элементтерді 0-ге айналдырады
ans =
1 2 3
0 5 6
0 0 9
>> hankel(a) % квадратты Ганкель матрицасы
ans =
1 4 7 2 5 8 3 6 9
4 7 2 5 8 3 6 9 0
7 2 5 8 3 6 9 0 0
2 5 8 3 6 9 0 0 0
5 8 3 6 9 0 0 0 0
8 3 6 9 0 0 0 0 0
3 6 9 0 0 0 0 0 0
6 9 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0
>> a=[1 2; 3 4]
a =
1 2
3 4
>> b=[5 6; 7 8]
b =
5 6
7 8
>> cat(2, a, b) % екі матрицаны жолдар бойынша біріктіру
ans =
1 2 5 6
3 4 7 8
>> [a, b] % екі матрицаны жолдар бойынша біріктіру
ans =
1 2 5 6
3 4 7 8
>> cat(1, a, b) % екі матрицаны бағандар бойынша біріктіру
ans =
1 2
3 4
5 6
7 8
>> [a;b] % екі матрицаны бағандар бойынша біріктіру
ans =
1 2
3 4
5 6
7 8
>> M=[2 1 -5 1; 1 -3 0 -6; 0 2 -1 2; 1 4 -7 6]
M =
2 1 -5 1
1 -3 0 -6
0 2 -1 2
1 4 -7 6
>> p=inv(M) % Матрицаның кері матрицасы
p =
1.3333 -0.6667 0.3333 -1.0000
-0.0741 0.2593 1.1481 -0.1111
0.3704 -0.2963 0.2593 -0.4444
0.2593 -0.4074 -0.5185 -0.1111
>> M*p % тексеру
ans
1.0000 -0.0000 -0.0000 0.0000
0 1.0000 0.0000 0.0000
0.0000 -0.0000 1.0000 -0.0000
0.0000 -0.0000 -0.0000 1.0000
Енді а векторының 5-ші элементін табайық, сосын 3-ші және 6-шы элементтер арасындағы сандарын 0-ге ауыстырайық:
>> а=[-1 3 -4 5 7 9 10 -2 8];
>> a(5)
ans=
7.000
>> a(3:6)=0
a=
-1 3 0 0 0 0 10 -2 8
Әдебиет: 1 нег.[51-106 ], 2 нег.[18-36], 3 нег.[85-100].
Бақылау сұрақтары:
1. Арифметикалық операторлар түрі
2. Векторларға қолданылатын функциялар
3. Матрицаларға қолданылатын функциялар
4. Блоктарды бөліп көрсету
5. Матрицаның бөліктерін алып тастау
6. Матрицаны визуализациялау