2.4.4. Пример выполнения расчёта трёхшарнирной арки

15 м

5

6

20

y

Требуется рассчитать симметричную арку ( рис. 2.65 ) согласно заданию, изло-

л

F₁

M

q

q

C

оженному на с. 110,

п

F₂

ри следующих исход-

н

A

B

f

V_A

V_B

H

H

K

ых данных: очертание

о си арки – круговое;

l / 2

l / 2

l = 60 м ; f / l = 1 / 6 ;

q = 8 кН / м ; F₁ = 40 кН;

F₂ = 18 кН; M = 40 кН ∙м. Рис. 2.65

Определение опорных реакций

а) вертикальные составляющие реакций опор:

 m_A = 0 V_B =  m_{A, F} / l = (q ∙15∙7,5 + F₁∙15 – M + q ∙20∙50 + F₂∙54)/60 =

= 177,2 кН;

 m_B = 0 V_A =  m_{B, F} / l = (q ∙20∙10 + F₁∙40 + M + q ∙15∙52,5 + F₂∙6)/60 =

= 160,8 кН;

Проверка:  y = 0 ( ? ) 177,2 – 8 ∙15 – 40 – 8 ∙20 – 18 +160,8 = 0;

б) распор:

(160,8 ∙20 – 8 ∙20∙10 –18 ∙ 6)/10 =168,4 кН;

Проверка: ( ? ) 168,4 ∙ 10 –160,8 ∙30 + 8 ∙15∙22,5 +

+ 40 ∙10 + 40 = 0.

Вычисление внутренних усилий в заданном сечении K

Предварительно по формулам из таблицы на с. 111 находим

радиус кривизны оси арки r, а затем – ординату y_K центра тяжести сечения K ( при x_K = 15 м ) и угол _K его наклона к вертикали:

 r = f / 2 + l ² / ( 8f ) = 10/2 + 60²/(8∙10) = 50 м;

 = 7,697 м;

 _K = arcsin [( l / 2 – x_K ) / r ] = 0,3047 рад ( = 17˚27" ).

Далее для использования формул ( 2.20 ) – ( 2.22 ) определяем балочные усилия M_{0, K} и Q_{0, K} в сечении K₀ балки того же пролёта, что и рассматриваемая арка, при такой же нагрузке ( рис. 2.66, б ), реакции которой V_{0, A} и V_{0, B} – такие же, как реакции V_A и V_B арки:

M_{0, K} = 160,8 ∙15 – 8 ∙15∙7,5 = 1512 кН∙м; Q_{0, K} = 160,8 – 8 ∙15 = 40,8 кН.

Находим изгибающий момент, поперечную и продольную

силы в сечении арки ( учитываем, что sin_K = 0,3; cos_K = 0,9539):

M_K = M_{0, K} – H∙y_K = 1512 – 160,8∙7,697 = 215,83 кН∙м;

Q_K = Q_{0, K} ∙cos_K – H∙sin_K = 40,8∙0,9539 – 168,4∙0,3 = – 11,60 кН;

N_K = – [Q_{0, K} ∙sin_K + H∙cos_K] = – [ 40,8∙0,3 + 168,4∙0,9539 ] =

= – 172,88 кН.

Построение эпюр внутренних силовых факторов в арке

Назначив расчётные сечения арки с шагом x = l / 8 = 7,5 м, используем компьютерную программу ARKA кафедры строительной механики НГАСУ (Сибстрин) для отыскания усилий M, Q и N в арке. В исходных данных следует указать:

– фамилия, инициалы: Sebeshev VG; номер группы: 300;

– очертание оси – окружность; арка симметричная;

– наличие затяжки – нет; расположение опор – на одном уровне;

– длина пролета l = 60; стрела подъёма f = 10; шаг сечений x = 7,5;

– число сосредоточенных нагрузок – 2; моментов – 1; равномер-

но распределённых нагрузок – 2; треугольных нагрузок – 0;

– координаты и значения нагрузок ( положительные F и q – вниз,

M – по ходу часовой стрелки ):

^*) В случае приложения момента

M бесконечно близко справа от

шарнира С следовало бы задать

a_M = l / 2 + 0,001.

F₁ = 40; a_F1 = 20; F₂ = 18; a_F2 = 20; M = – 40; a_M = 29,999^*);

q₁ = 8; a_q1 = 0 (начало); b_q1 = 15 (конец);

q₂ = 8; a_q2 = 40 (начало); b_q2 = 60 (конец).

Результаты компьютерного счёта:

РАДИУС КРИВИЗНЫ ОСИ АРКИ R = 50.0000

ОПОРНЫЕ РЕАКЦИИ: ВЕРТИКАЛЬНЫЕ VA = 160.8000 VB = 177.2000 РАСПОР H = 168.4000

№ сечения	Абсцисса сечения X (м)	Ордината сечения Y (м)	Угол наклона сечения Т (rad)	Внутренние силовые факторы в сечении
				Изгибающий момент М	Поперечная cила Q	Продольная cила N
1	0.000	0.000	0.6435	0.0000	27.6000	– 231.5993
2	7.500	4.651	0.4668	197.6996	14.2373	– 195.7460
3	15.000	7.697	0.3047	215.8319	– 11.5993	– 172.8834
4	20.000	8.990	0.2014	202.1185	6.2957	– 173.1576
5	20.000	8.990	0.2014	202.1185	– 32.8962	– 165.1576
6	22.500	9.434	0.1506	129.2639	– 24.4691	– 166.6147
7	30.000	10.000	0.0000	40.0000	0.8000	– 168.4000
8	30.000	10.000	0.0000	0.0000	0.8000	– 168.4000
9	37.500	9.434	– 0.1506	101.2639	26.0509	– 166.3747
10	45.000	7.697	– 0.3047	299.8319	13.1256	– 172.4034
11	52.500	4.651	– 0.4668	293.6996	– 12.8084	– 195.0260
12	54.000	3.863	– 0.4668	268.5993	– 16.7203	– 201.1080
13	54.000	3.863	– 0.5007	268.5993	– 32.5111	– 209.7480
14	60.000	0.000	– 0.6435	0.0000	– 40.7200	– 241.0400

назначены по два смежных сечения.

Примечание: в местах приложения сосредоточенных сил и момента автоматически

F₁ = 40 кН

M = 40 кН∙м

q = 8 кН/м

C

q = 8 кН/м

Эпюры M, Q, N в арке представлены на рис. 2.66, в – д (мас-штабы ординат Q и N отличаются в 5 раз). Для сравнения на рис. 2.66, е, ж приведены эпюры усилий M₀ и Q₀ в балке со схемой по рис. 2.66, б ( в десятикратно уменьшенном масштабе ординат ).

F₂ = 18 кН

а)

f = 10 м

V_A = 160,8 кН

K

V_B = 177,2 кН

y_K

_K

A

B

H = 168,4 кН

H

x = 7,5 м

7,5

7,5

7,5

7,5

2,5

5

2,5

5

1,5

6

F₁

F₂

M

q

q

V_{0, A}

V_{0, B}

C₀

А₀

B₀

б)

M

( кН∙м )

в)

Q

г)

16,72

( кН )

N

д)

( кН )

919,2

M₀

е)

1692

1512

1716

1724

1684

160,8

( кН∙м )

Q₀

0,8

40,8

129,2

111,2

( кН )

ж)

Р

177,2

ис. 2.66

При построении эпюр нужно пользоваться правилами, изложенными на с. 19 – 21 и 105 ) и следить за соответствием изломов на эпюре М приложенным сосредоточенным нагрузкам ( на эпюрах Q и N в этих точках – разрывы ), на эпюре Q – границам участков нагрузок q; нулевых точек эпюры Q – экстремумам М ; в точке приложения внешнего момента – скачок на эпюре М.

Линии влияния силовых факторов в арке и их загружение

Линии влияния распора и усилий в сечении K строим как типовые ( см. с. 108 ). Характерные ординаты линий влияния:

= 15∙[1 – (15 + 30∙7,697/10)/60] = 5,4772 м;

= (15 – 30∙7,697/10) ∙30/60 = –4,0455 м;

= 0,9539 ∙ (1 – 15/60) –

– 0,3 ∙30 ∙15/(10 ∙60) = 0,4904; = – 0,4635;

= 0,9539 ∙30/60 – 0,3 ∙30 ∙30/(10 ∙60) =

= 0,0270;

= – [0,3 ∙ (1 – 15/60) +

+ 0,9539∙30 ∙15/(10 ∙60) = –0,9404; = – 0,6404;

= – [0,3 ∙ 30/60 +

x_K =15 м

F = 1

C

K_M

+ 0,9539∙30 ∙30/(10 ∙60) = –1,5808.

K

Линии влияния, по-

с

B

f

_K

y_K

K_Q

троенные по

A

V_A

V_B

вычислен-

н ым ординатам,

H

H

пред-

с

a = l / 2 = 30 м

b = l / 2 = 30 м

тавлены на рис. 2.67.

Д

30 ∙30/(10 ∙ 60) =

= 1,5

ля контроля положения

и

0,75

х нулевых точек можно

и

Л.В. H

спользовать отрезки a_KM

и

Л.В. M_K ( м )

5,4772

a_KQ ( рис. 2.67 ) – рассто-

я

a_KM

ния по горизонтали от

л евой опоры до момент-

н

Л.В. Q_K

4,0455

0,0270

ых точек (см. с. 109) K_M

0,4904

и

= 23,628 м;

= 30,872 м.

K_Q:

0,4635

a_KQ

Л.В. N_K

0,6404

1,5808

0,9404

Рис. 2.67

Указание: в случае расположения сечения K справа от вершины арки расстояния a_KM и a_KQ следует отмерять от правой опоры, а в

формулы для их определения подставлять a вместо b, l – x_K вместо x_K и брать tg _K по абсолютной величине.

Для загружения линий влияния в дополнение к ординатам, обозначенным на рис. 2.67, вычисляем ординаты в точках приложения сосредоточенных нагрузок F₁ и F₁ и на левом краю правой нагрузки q, а также тангенсы углов наклона средних участков Л.В.: y_{H, F1} = 1; y_{H, F2} = 0,3; y_{H, q} = 1; tg _H = 0,05;

y_{MK, F1} = 2,3031; y_{MK, F2} = – 0,8091; y_{MK, q} = – 2,6970; tg _MK = – 0,6348;

y_{QK, F1} = 0,3359; y_{QK, F2} = 0,0054; y_{QK, q} = 0,0180; tg _QK = – 0,0309;

y_{NK, F1} = – 1,1539; y_{NK, F2} = – 0,3162; y_{NK, q} = – 1,0538; tg _NK = – 0,0427.

Загружаем линии влияния заданной нагрузкой ( см. ( 1.23 )):

Н = 40∙1+8∙0,75∙15/2 +(– 40)∙ 0,05 +8∙1∙20/2+18∙0,3 = 168,40 ( кН );

M_K = 40∙2,3031+8∙5,4772∙15/2 +(– 40)∙(– 0,6348) +8∙(– 2,6970)∙20/2+

+18∙(– 0,8091) = 215,82 ( кН∙м );

Q_K = 40∙0,3359+8∙(–0,4635)∙15/2 +(– 40)∙(– 0,0309) +8∙ 0,0180∙20/2+

+18∙ 0,0054 = – 11,60 ( кН );

N_K = 40∙(–1,1539) + 8∙(–0,6404)∙15/2 + (– 40)∙(– 0,0427) +

+ 8∙ (–1,0538)∙20/2 +18∙ (–0,3162) = – 172,87 ( кН ) – практически полное совпадение с ранее найденными значениями.

Матрица влияния силовых факторов в арке

Схема расчётных точек для формирования матрицы влияния

п

1 2 3 4 5

1

2

3

риведена на рис. 2.68, а. Под сече-

н

15 м 15 м 30 м 5

ием K, где на Л.В. Q_K и N_K имеют- а)

с

F₁

F₂

M

q

q

я разрывы, назначены две расчёт-

н ые точки. Приведение заданных

н

F₍₁₎

F₍₃₎

F₍₂₎

F₍₅₎

F₍₄₎

агрузок к эквивалентным в расчёт- б)

н ых точках показано на рис. 2.68, б.

F

Рис. 2.68

₍₁₎ = F₍₂₎ = q∙15/2 = 60; F₍₃₎ = F₁ +

+ M/15 = 29,333; F₍₄₎ = F₍₄₎₂ + F₍₄₎₃ =

= F₁ /3 – M/15 + q∙20/3 + F₂ /5 = 67,6; F₍₅₎ = q∙20/3 + F₂ = 49,956.

60

60

F_u = 29,333

67,6

49,956

Матрица влияния силовых факторов и вектор расчётных узловых нагрузок:

.

Вектор искомых усилий S = [ H M_K Q_K N_K ] ^т находится матричной операцией S = _S F_u = [ 168,40 215,82 –11,60 –172,87 ] ^т.

Формирование системы уравнений статики

на основе конечно-элементной модели арки

Используем расчётную схему элементов и узлов арки, представленную на рис. 2.60, б, задавая a = b = 30 м; y_C = 10 м; y_B = 0; cos ₀ = 0,8 = cos _l ; sin ₀ = 0,6 = sin _l – знак _l учтён в матрице A ( см. с. 107 ) , которая принимает вид

m

x

y

m

x

y

x

y

x

y

x

y

 =

2

1

Q_b1 N_b1 Q_e1 N_e1 Q_b2 N_b2 Q_e2 N_e2 V_A H_A V_B H_B

		– 30	– 10
	– 1	– 0,6	0,8
1		– 0,8	– 0,6
						– 30	10
					– 1	0,6	0,8
				1		– 0,8	0,6
0,6	0,8								1
– 0,8	0,6							1
			– 1				1
		1				– 1
				0,6	– 0,8						–1
				0,8	0,6					1

1

2

3

Вычисляем компоненты вектора свободных членов B_F уравнений равновесия по шаблону, приведённому на с. 107:

= – q ∙15∙7,5 – F₁∙20 + M = –1660; = – (q ∙15 + F₁) sin ₀ = – 96;

= – (q ∙15 + F₁) cos ₀ = –128; = q ∙20∙10 + F₁∙6 =1708;

= – (q ∙20 + F₂) sin _l = –106,8; = (q ∙20 + F₂) cos _l = 142,4;

F_2x= F_2y = 0, тогда B_F = [–1660 –96 –128 1708 –106,8 142,4 0 0 0 0 0 0 ]^т.

Решение системы A∙S + B_F = 0 даёт S = [ 27,60 –231,20 0,80 –168,40 –40,72 –241,04 0,80 –168,40 160,80 168,40 177,20 168,40 ]^т – полное совпадение со значениями, полученными ранее.

Ф а к у л ь т а т и в н о:

Определение усилий в арке при очертании оси, отличном от заданного

23_2.3

24_2.3

Значения реакций связей трёхшарнирной системы обусловлены нагрузкой, вза-имным расположением шарниров, размерами l и f , но на них не влияет форма оси арки или рамы. При этом внутренние силовые факторы в сечениях существенно зависят от очертания оси, задаваемого выражением y(x) – это видно из формул ( 2.20 ) – ( 2.22 ). Варьируя форму оси, можно получать выгодное распределение усилий в системе и даже добиваться безмоментности арки или рамы, т. е. равенства нулю моментов во всех сечениях при заданной нагрузке: M(x) 0. Такая трёхшарнирная система называется системой с рациональным очертанием оси; в её сечениях возникают только продольные силы. В случае вертикальной нагрузки, когда M(x) = M₀ (x) – H∙y(x), условие безмоментности даёт уравнение рациональной оси: y_r(x) = M₀ (x) /H – до постоянного множителя H ^–1 = f / M_{0, C} форма оси безмоментной арки или рамы совпадает с очертанием балочной эпюры изгибающих моментов.

26_2.3

При многокомпонентных нагрузках рациональная форма оси может быть трудноосуществимой в изготовлении реальных конструкций – тогда назначается одно из типовых очертаний, близкое к рациональному. Для арок можно руководствоваться следующими соображениями:

 при нагрузках, примерно равномерно распределённых по длине пролёта, целесообразно выбирать параболическое очертание;



28_2.3

если нагрузки располагаются в основном в средней части пролёта, то ближе к рациональной будет синусоидальная или параболическая форма оси;

 в случае, когда нагрузки приложены преимущественно в приопорных зонах, более выгодной является арка в форме дуги окружности или половины эллипса.

F₁

M

q

C

q

137,61

Для арки с нагрузками, заданными в рассматриваемом примере ( см. рис. 2.66 ), выполним расчёт внутренних усилий при эллиптическом очертании оси. Используя программу ARKA, в исходных данных изменяем только один компонент – описание формы оси. Результаты компьютерного счёта представлены в виде эпюр M, Q, N на рис. 2.69. Там же для сравнения штриховыми линиями показаны усилия в круговой арке, найденные в основном решении задачи.

F₂

а)

f = 10 м

V_A

V_B

H

H

A

B

7,5

7,5

7,5

7,5

7,5

5

5

6

2,5

2,5

1,5

132,86

M

( кН∙м )

36,86

91,20

53,61

87,47

128,31

59,47

Q

( кН )

N

( кН )

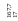
Рис. 2.69

Эпюры изгибающих моментов в двух арках, различающихся только формой оси, сильно отличаются друг от друга, во-первых, по общему виду ( в круговой арке моменты все положительные, в эллиптической – разнозначные ), а во-вторых – по наибольшим абсолютным значениям моментов ( в эллиптической – почти в 1,5 раза меньше ). Продольные силы в двух арках на большей части длины почти одинаковые; значительные расхождения только вблизи опор, причем меньшие N – также в эллиптической арке.

Читателю предлагается самостоятельно убедиться в том, что в арке с осью по параболе 2-й степени или синусоиде, изгибающие моменты существенно больше, чем при двух рассмотренных выше очертаниях оси – по окружности и эллипсу.