Основные правила построения и проверки эпюр m и q

В нешние силовые факторы	С M осредоточенный момент	Сосредоточенная сила	Равномерно распределённая н q агрузка
Схема нагрузки	. x . . . . .	F . l x . . . . .	l b b x . . . . . .
Эпюра изгибающих м В точке приложения момента – скачок на М оментов M	M  	r В точке приложения cилы – излом в направлении её действия Плавное (без излома) сопряжение прямой линии и квадратной параболы	 Mmax Прямая Парабола
Эпюра поперечных сил Q	Q = tg  Q На эпюре Q – никаких особенностей Скачок на –F в точке приложения силы	Ql = tg l Qr = tg r Q = – F	Q = tg   Ql = tg l Излом  tg = – q  b
Дифференциаль- ные зависимости между M, Q и q	M + dM Q + dQ M q dxq Очертание эпюр в пределах грузового участка: 1. На незагруженном участке ( q = 0 ): эпюра М – прямолинейная, эпюра Q – постоянная. 2. На участке с равномерно распределённой нагрузкой ( q = const ): – эпюра М – квадратная парабола, выпуклая в направлении действия нагрузки, эпюра Q – наклонная прямая; – в точке, где Q = 0, на эпюре М – экстремум ( Mmax или Mmin ).

Примечание: направление равномерно распределённой нагрузки q в таблице (сверху вниз) отражает гравитационную природу большинства

нагрузок на строительные конструкции. Согласно рис. 1.14, q_y (x) = – q .

50

О дифференциальных уравнениях равновесия для плоского криволинейного стержня и их использовании в расчётах арок – в п. 2.4.1 ( с. 105 ).

В таких типовых системах, как балки, рамы, комбинированные, могут присутствовать элементы в виде простых балок (однопролётных шарнирно опёртых по концам или консольных ) – эпюры изгибающих моментов и поперечных сил в них от основных видов нагрузок представлены в табл. 1.2. Их можно использовать как стандартные, в сочетании с принципом независимости воздействий ( суперпозиции, аддитивности ), для определения усилий в балочных элементах от групп нагрузок. Например, раз-ложив заданную нагрузку ( рис. 1.15, а ) на типовые составляющие ( рис. 1.15, б – г ), усилия от каждой из них находим по табл. 1.2 ( рис. 1.15, д – ж ). Складывая усилия от составляющих нагрузок, получаем искомые эпюры M и Q ( рис. 1.15, з, и ).

F

q

F

q

q

а) б) в) г)

a

= + +

c

l

M

д) е) ж)

+

+

+

+

з)

Q

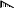
и)

Рис. 1.15

Q_b

F

q

M_e

Замечание: поперечные силы от составляющих нагрузок можно не определять, а полные Q на части балки между опорами вычислять из условий равновесия

п

M_b = 0

о схеме рис. 1.16, используя найден-

н

b

e

ый момент M_e :



l

a

Q_e

m_b = 0 Q_e = M_e / l – ( Fa /l + ql /2 );

 y = 0 Q_b = ql /2 + F ( 1 – a /l ).

Рис. 1.16

Таблица 1.2