1 .3.1. Статический метод

п

45

редусматривает использование уравнений равновесия системы в целом и её частей.

Количество уравнений n_y для СОС всегда совпадает с числом n_c искомых реакций связей – это следует из условия W = 0, откуда n_ = n_c , где n_ – суммарное число степеней свободы расчётных дисков (включая назначенные подэлементы), освобождён-ных от всех связей; причём, согласно общим принципам механи-ки, количество уравнений статики равно числу степеней свободы несвязанных элементов системы: n_y = n_ , тогда для СОС n_y = n_c .

^**) Например, даже для одного стержня три уравнения равновесия в плоскости можно записать как

m_A = 0, m_A = 0, m_A = 0,

y = 0, либо m_B = 0, либо m_B = 0,

x = 0, y = 0, m_C = 0.

Расчётные уравнения статики могут записываться по-разно-му^**). Существуют два альтер-

нативных способа получения

у равнений:

1) с использованием спе-

цифических особенностей си-

стемы того или иного типа ( балки, фермы и др.) для построения рациональной последовательности уравнений, не требующих их одновременного совместного решения, вследствие чего в ряде случаев удаётся на каждом шаге расчёта из одного уравнения находить одну новую реакцию связи или, в крайнем случае, решать системы с небольшим числом ( 2 – 3 ) неизвестных, что при-влекательно при выполнении «ручного» расчёта. Общий принцип этого подхода: расчёт выполняется в последовательности, обратной порядку образования (синтеза) рассчитываемой системы, выявленному в структурном анализе расчётной схемы;

2) формирование полной системы уравнений равновесия на основе конечно-элементного представления расчётной схемы сооружения ( конструкции ), с применением общего алгоритма для всех систем, независимо от их особенностей ( плоская или пространственная, рама, ферма и т.д.).

46

Применение первого способа рассматривается далее в главе 2 для каждого типа плоских стержневых систем.

Общий алгоритм второго способа таков:

а)

б)

в)

1. В расчётной схеме системы выделяются элементы ( пря-мые или криволинейные стержни конечной длины ) и узлы – области бесконечно малых размеров, назначаемые по следующим признакам: а) места соединения

э

ds

лементов ( рис. 1.9, а, б ) или из-

л

д)

ома оси стержня ( рис. 1.9, в );

б ) места расположения внешних

с

г)

е)

вязей ( опор ) – рис. 1.9, г, д;

в

ж)

) концы консолей ( рис. 1.9, е );

г ) дополнительно – любые точки

( сечения ) стержней ( рис. 1.9, ж ).

Рис. 1.9

2. Производится нумерация

элементов j = 1, 2, …, n_el и узлов

t

4

5

q

= 1, 2, …, n_u с обозначением на схеме ( номера элементов – в кружкáх, узлов – в треугольниках ); в прямоугольниках проставлются номера опорных связей j₀ = 1, 2, …, C₀ –

п

4

5

B

6

ример дан на рис. 1.10.

3

1 … 3

4

3. Сечениями стержней, бес-

к

2

1

n_el = 5

n_u = 6

C₀ = 4

F

онечно близкими к узлам или

(

A

что то же самое ) к концам эле-

м

2

1

3

ентов ( концевыми сечениями ),

с

Рис. 1.10

истема разделяется на элемен-

ты и узлы ( внутренние и опорные );

одновременно с этим удаляются или рассекаются опорные связи.

^*) Концевые усилия равны реакциям конце-вых связей, которыми элемент соединяется в узле с другими элементами.

4. К концам элементов и всем узлам прикладываются усилия в концевых сечениях элементов (концевые усилия^*) ), а к опор-ным узлам – также реакции

опор; кроме того, к элементам

прикладываются внеузловые

н

Q_b4

Q_e4

Q_b5

Q_e5

агрузки, к узлам – заданные в узлах сосредоточенные нагрузки (силы и моменты). Результат выполнения процедур 3 и 4 представлен на рис. 1.11.

4

5

q

q

V_B

N_e3

M_e4

M_b4

M_b5

M_e4

M_e5

Q_e5

6

M_e3

4

5

Q_e3

Q_e4

N_b4

N_e4

N_b5

M_b4

N_e5

M_b5

M_e5

Q_b4

Q_b5

Символами b_j и e_j обозначены начало и конец

j-го элемента

N_e3

N_b3

Q_e3

M_e3

M_b3

3

Q_bj

M_bj

N_ej

M_ej

j

N_bj

b_j

Q_b3

e_j

F

Q_ej

Q_b1

M_b1

M_A

M_e1

Q_e1

Q_b2

Q_e2

M_e2

M_b3

Q_b3

M_e2

M_b2

2

1

1

N_b1

H_A

N_e1

N_b2

N_e2

3

2

Q_b2

M_b2

Q_e2

M_b1

Q_b1

V_A

Q_e1

Р

44

ис. 1.11

( 1.2 )

5. Формируется полная система уравнений равновесия для разделённых элементов и узлов, в матричной записи –

г

ров – концевых усилий S_K и реакций опор R;

де S = – вектор подлежащих определению силовых факто-

A – квадратная матрица коэффициентов при неизвестных S ;

B_F – вектор характеристик влияния заданных нагрузок.

Вектор концевых усилий формируется как

S_K = [ ] ^Т, ( 1.3 )

где S_Kj – вектор усилий в концевых сечениях j-го элемента;

для плоской системы S_Kj = [ M_bj Q_bj N_bj M_ej Q_ej N_ej ] ^Т ( на-

поминаем: […] ^Т – символ транспонирования матрицы );

при этом общее число компонентов S_K равно 6 n_el ;

R = [ R₁ R₂ … R_Co ] ^Т – вектор компонентов опорных реакций

( для схемы по рис. 1.11 R = [ M_A V_A H_A V_B ] ^Т ).

47

Общее число неизвестных S в уравнениях ( 1.2 ) в случае плоской системы n = 6 n_el + С₀ ( в примере n = 6∙5 + 4 = 34 ).

Структура матрицы А определяется тем, что полная система ( 1.2 ) состоит из трёх частей:

1) уравнения равновесия элементов A_el S_K + B _{el, F} = 0; ( 1.2 а )

2) уравнения равновесия узлов A_u S + B _{u, F} = 0; ( 1.2 б )

3) условия шарнирного соединения элементов

A_h S_K = 0, ( 1.2 в )

поэтому поблочная матричная запись ( 1.2 ) имеет вид

, ( 1.4 )

где A_el – матрица коэффициентов при концевых усилиях S_K в урав-

нениях равновесия элементов;

A_{u, K} и A_{u, R} – матрицы коэффициентов соответственно при уси-

лиях S_K и опорных реакциях R в уравнениях равновесия

узлов;

A_h – матрица коэффициентов, равных единице, в условиях ра-

равенства нулю изгибающих моментов в концевых сече-

^*) Если в узле шарнирно соединены два элемента ( рис. 1.9, б ), то приравнивается 0 концевое усилие в одном из них; при соединении трёх элементов – в двух и т.д.

ниях элементов, прикрепленных к узлам цилиндрически-

ми шарнирами^*) ( в случае по-

ступательного шарнира при-

равнивается нулю продоль-

ная или поперечная сила );

B _{el, F} – вектор характеристик влияния заданных внеузловых на-

грузок в уравнениях равновесия элементов;

B _{u, F} – то же, узловых нагрузок в уравнениях равновесия узлов.

Уравнений 1-й группы для плоской системы 3 n_el ( в рассматриваемом примере – 15), 2-й группы – 3 n_u ( в примере – 18 ), уравнений 3-й группы для статически определимой системы должно быть 3 ( n_el – n_u ) + С₀ ( для рамы по рис. 1.10 – 1).

В матрицах A_el , A_{u, K} и A_h количество столбцов равно общему числу концевых усилий S_K , т. е. 6 n_el , а строк в них соответственно столько, сколько уравнений 1-й, 2-й и 3-й групп. Число компонентов матрицы B_{el, F,} равно 3 n_el , а B_{u, F} – 3 n_u .

Матрица A_el имеет блочно-диагональную структуру: A_el =

= diag [ ], где A_j – матрица размера 3×6, её ком-

поненты находятся из рассмотрения стандартной схемы j-го пря-молинейного элемента ( рис. 1.12 ), уравнения равновесия которого в собственной ( локальной ) системе координат имеют вид

_m_bj = 0 – M_bj – Q_ej l_j + M_ej + _m_{bj, F} = 0,

_x_j = 0 – N_bj + N_ej + _x_{j, F} = 0, ( 1.5 )

_y_j = 0 Q_bj – Q_ej + _y_{j, F} = 0,

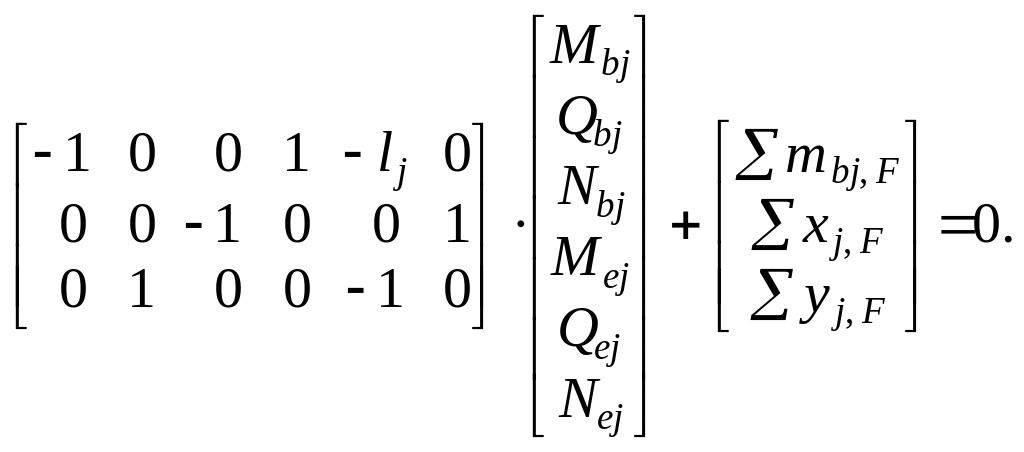
в матричной форме:

( 1.6 )

B_{el, Fj}

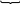
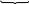
A_j

S_Kj

В ( 1.5 ) и ( 1.6 ) _m_{bj, F} , _x_{j, F} и _y_{j, F}

определяются от заданной нагрузки.

N_bj

Q_ej

N_ej

M_ej

x_j

y_j

c_qj

q_xj

e_j

F_xj

a_qj

q_yj

M_j

F_yj

Из ( 1.6 ) видно, что матрицы A_j ( j = 1, 2, …, n_el ) различаются только одним компонен-

том – длиной l_j . Вектор B_{el, Fj} ха-

рактеристик влияния внеузловых нагрузок j-го элемента, согласно схеме рис. 1.12, при наличии на элементе нескольких нагрузок

j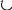

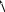
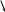
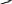
Q_bj

l_j

b_j

M_bj

a_Fj

a_Mj

Рис. 1.12

каждого типа может быть представлен как

. ( 1.7 )

Из блоков B_{el, Fj} ( j = 1, 2, …, n_el ) формируется вектор

B_{el, F} = [ ] ^Т. ( 1.8 )

В рассматриваемом примере получается:

(15×30)

(15×1)

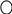
_{j – 1}

_{j – 1, t t}

y

Коэффициенты A_u и свободные члены B_{u, F} уравнений 2-й группы определяются из условий равновесия узлов. Для узла с номером t уравнения статики _m^(t) = 0, _x^(t) = 0, _y^(t) = 0 в общих для всей системы ( глобаль-

н

_{j, t}

ых ) координатных осях записы-

в

N_Kj

N_{K, j – 1}

Q_{K, j – 1}

аются в соответствии со схемой,

п

t

M_Kj

M_{K, j – 1}

_j

риведённой на рис. 1.13:

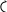
F_{x, t}

Q_Kj

_m^(t) = 0 _M_Kj – M_t = 0, ( 1.9 )

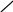
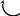
M_t

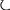
_x^(t) = 0 _N_Kj cos _j +

F_{y, t}

+ _Q_Kj sin _j + F_{x, t} = 0, ( 1.10 )

x

0

_y^(t) = 0 _N_Kj sin _j –

Рис. 1.13

– _Q_Kj cos _j +F_{y, t} = 0, ( 1.11 )

где суммирование выполняется по

всем элементам, примыкающим к t-му узлу, а символ K_j обозначает то концевое сечение j-го элемента ( b_j или e_j ), которое, согласно схеме ( рис. 1.11 ), расположено у данного узла. Для системы с ортогональными элементами синусы и косинусы углов наклона их осей равны 1 или 0. Если узел t опорный, то к нему прикладываются также реакции опор ( в общем случае – горизонтальная, вертикальная и момент ), которые дополнительно включаются в уравнения ( 1.9 ) – ( 1.11 ). Свободные члены уравнений равновесия узлов составляют вектор

B_{u, F} = [ – M₁ F_{x, 1} F_{y, 1} – M₂ F_{x, 2} F_{y, 2} … – M_t F_{x, t} F_{y, t} … ]^т.

В примере-иллюстрации первые части блока A_u = [ A_{u, K} A_{u, R} ]

м

Узлы

атрицы коэффициентов A и вектора B_{u, F} имеют вид

A

. . . . . . . . . . . . . . . . . . . . . . .

Реакции опор

M_A H_A V_A V_B

2

1

3

(18×34)

(18×1)

_u =

Э

2

3

1

лементы

A_{u, K} A_{u, R}

Уравнения 3-й группы записываются как равенства нулю некоторых концевых усилий для элементов, шарнирно примыкающих к узлам ( момента в случае цилиндрического шарнира, продольной или поперечной силы у поступательного шарнира ). Таких условий для рамы по схеме рис. 1.10 должно быть 1 ( см. с. 14 ). Оно формулируется для сечения e₁ 1-го элемента у шарнирного узла 2: M _e1 = 0. Можно вместо этого записать M _b2 = 0 ( но не одновременно! ). Матрица A_h – строка с 1 в 4-й позиции:

A_h = [ 0 0 0 1 0 0 … 0 0 ].

З а м е ч а н и е : уравнения 3-й группы можно вообще не составлять, если в вектор неизвестных S не включать заведомо нулевые концевые усилия ( здесь – M _e1 или M _b2 ) .

Изложенный алгоритм задаёт последовательность процедур формирования полной системы уравнений равновесия для отыскания усилий, единую для всех статически определимых систем. Дополнительный учёт характерных особенностей систем разных типов ( балок, ферм ), как правило^*), приводит к упрощению расчётных операций и формул алгоритма – подробнее это будет рассмотрено в дальнейшем применительно к каждому из типов плоских стержневых систем.

^*) Исключение – арки, из-за криволинейного очертания осей элементов.

Составленная по общему алгоритму система уравнений ( 1.2 ) решается известными из линейной алгебры методами, реализованными в доступных компьютерных программах; в результате находится вектор искомых силовых факторов ( концевых усилий и реакций опор ):

48

, ( 1.12 )

п ричём математически необходимое и достаточное условие Det ( A ) 0 существования единственного и однозначного решения является также и достаточным аналитическим условием геометрической неизменяемости рассчитываемой статически определимой системы.

Найденные концевые усилия далее используются для оп-

ределения внутренних силовых факторов M(x_j), Q(x_j), N(x_j) в лю-

б

44

ых сечениях элементов ( по схеме рис. 1.12 ) – способами, известными из курса сопротивления материалов. Эта часть расчёта, с построением эпюр M, Q, N, в задачах строительной механики является «техническим» этапом и могла бы вообще не обсуждаться. Тем не менее, далее воспроизводятся основные положения методики построения эпюр внутренних усилий с применением уравнений статики, записанных в дифференциальной форме.

Q(x)

y

14_2.2

Дифференциальные уравнения равновесия для прямолинейного стержня при его растяжении ( сжатии ) и прямом поперечном изгибе в главной плоскости x0y ( схема стержня и его элементарного участка dx – на рис. 1.14 ) записываются как

M(x)

M(x) + dM(x)

q_x (x)

N(x)

N(x) + dN(x) N(x)x)

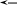
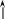
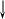
; ( 1.13 )

Q(x) + dQ(x)

dx

q_y (x)

x

x

0

; ( 1.14 )

dx

Рис. 1.14

. ( 1.15 )

Объединение ( 1.14 ) и ( 1.15 ) даёт разрешающее уравнение

, ( 1.16 )

и

49

з которого следуют известные из курса сопротивления материа-

л ов свойства функции M(x) в пределах грузового участка:

 на незагруженном участке ( свободном от распределённой поперечной нагрузки, т. е. при q_y (x) = 0 ) M(x) – линейная функция ( при этом, согласно ( 1.15 ), Q(x) = const );

 на участке, где приложена равномерно распределённая поперечная нагрузка q_y (x) = const = q , M(x) – квадратичная функция, а Q(x) – линейная.

Аналогично из уравнения ( 1.13 ): на участке без продольной распределённой нагрузки ( q_x (x) = 0 ) продольная сила N(x) = const, а на участке с равномерной нагрузкой q_x (x) = const = q – линейно переменная N(x).

Вышеизложенные правила позволяют строить эпюры из-гибающих моментов, продольных и поперечных сил в пределах грузового участка без записи аналитических выражений M(x), Q(x) и N(x):

 в случае линейного закона изменения соответствующей величины достаточно вычислить её значения в двух сечениях грузового участка ( обычно по его концам );

 квадратичная эпюра M на участке с нагрузкой q строится по трем ординатам – концевым и посредине.

Напомним, что на участке с прямолинейной эпюрой М соответствующая постоянная поперечная сила Q, согласно ( 1.14 ), может вычисляться как тангенс ( размерный ) острого угла  наклона эпюры M, отсчитываемого от оси эпюры ( если  – по ходу часовой стрелки, то Q > 0 ).

На границах грузовых участков прямолинейного стержня в местах приложения сосредоточенных внешних сил и моментов на эпюрах изгибающих моментов M, поперечных и продольных сил Q и N имеются особенности – разрывы ( скачки ) и изломы. Основные правила, описывающие форму ( прямая, кривая ) и осо-бенности эпюр M и Q , сведены в таблицу 1.1 – ими нужно пользоваться при построении и проверке эпюр для прямолинейных стержней при нагрузках F и q , перепендикулярных к оси стержня.

Таблица 1.1