2.2.4. Пример выполнения расчёта многопролётной балки

Р

F₁

F₂

F₃

асчётная схема ( рис. 2.9 ) и исходные данные

F

q

F

p

a /2

a /4

M

1

a

a

a

a

2a

a

a

A

a/2

a/2

Рис. 2.9

a = 2 м; F = 15 кН; M = 16 кН∙м; q = 12 кН /м;

p = 10 кН /м; F₁ = 8 кН; F₂ = 12 кН; F₃ = 10 кН .

Кинематический анализ расчётной схемы

а

D₁

D₂

D₃

D₄

H₁

H₂

H₃

) проверка выполнения необходимого условия геометрической неизменяемости системы ( 1.1 ) – количественный анализ:

с

K

огласно рис. 2.10,

D

«з е м л я»

= 4, H = 3, С = 0,

С

Рис. 2.10

₀ = 6, тогда

W = 3D – 2H – C – C₀ = 3∙4 – 2∙3 – 0 – 6 = 0 – условие ( 1.1 ) выполне-

но, следовательно, система может быть геометрически неизменяемой; дополнительно: условие ( 2.1 ) также выполняется: 6 = 4 + 2 ;

б) структурный анализ расчётной схемы:

так как ни у одного диска нет трёх связей с диском «земля» ( рис. 2.10 ), то рассматривать соединение двух дисков типовым способом ( рис. 1.2, б, в ) невозможно; поэтому пытаемся применить приём соединения трёх дисков – в схеме балки можно усмотреть соединение дисков D₃ , D₄ и «земля» с помощью трёх пар связей первого типа ( по рис. 1.2, г ) – двух параллельных опорных связей между «землёй» и D₃ , двух в виде неподвижной шар-нирной опоры диска D₄ и двух в виде цилиндрического шарнира, связывающего диски D₃ и D₄ , причём три точки попарного пересечения осевых линий связей не располагаются на одной прямой ( первая – бесконечно удалённая по вертикали, а две остальных – на горизонтальной оси балки ), следовательно, связи наложены правильно, и, поскольку один из соединяемых дисков – это «земля», в результате получается геометрически неизменяемая система ГНС₁ = D_I = D₃ + D₄ + «земля», которая далее таким же способом соединяется с дисками D₁ и D₂ : D_II = D_I + D₁ + D₂ без дефектов в расположении связей^*); результат – геометрически неизменяемая система ( за-

д

^*) Второй шаг синтеза системы можно истолковать по-другому: как присоединение диска D₁ к ГНС₁ с помощью трёх линейных связей (по спо-собу рис. 1.2, б ), если диск D₂ считать связью.

анная балка ).

Дополнительно: взаимное распо-

ложение опор и шарниров удовлетворя-

ет требованиям, изложенным на с. 48.

Вывод: рассматриваемая балка геометрически неизменяема и статически определима ( W = 0 ).

Рабочая схема балки

ВЧ₁

ВЧ₂

Как следует из структурного анализа, образование балки осуществляется в несколько действий ( шагов), приводящих к по-следовательному возникновению геометрически неизменяемых систем – т. е. МСОБ является составной системой с главными и второстепенными частями ( см. с. 8 ). Но, как уже отмечалось ранее, ни у одного из элементов балки нет трёх связей с «землёй», поэтому безусловно главных частей нет ( см. с. 49 ). Тем не менее, диски D₁ и D₃ ( рис. 2.10 ) – условно главные части ( каждая из них соединена с «землёй» двумя вертикальными связями и может воспринимать любую вертикальную нагрузку даже при отсутствии всех других частей ). Диски D₂ и D₄ – независимые друг от друга второстепенные части ( они разделены условно главной частью ). Изображая глав-

ные и втор

УГЧ₂

УГЧ₁

остепенные ча-

с ти на разн ых уровнях

( см. с. 49 ),

Рис. 2.11

получаем рабо-

чую схему балки ( рис. 2.11 ).

Расчёт МСОБ на действие постоянной нагрузки

Показываем на рабочей схеме балки заданную постоянную нагрузку, компоненты которой – q , M и две одинаковых силы F ( рис. 2.12, а ); освобождаем балочные части системы ( главные и второстепенные ) от внешних ( с «землёй» ) и внутренних ( между стержнями ) связей, взамен которых прикладываем их реакции ( рис. 2.12, б, в, г, д ), следя за тем, чтобы одноимённые реакции, действующие на соединявшиеся в шарнире части, были изображены противоположно направленными. Силу F, показанную на исходной схеме ( рис. 2.9 ) приложенной к шарниру с, следует сместить на dx в любую сторону – влево или вправо, вследствие чего она оказывается на одной из частей балки ( здесь выбрано – на УГЧ₁ ). Смещать точку приложения сосредоточенного момента M нельзя – в решаемой задаче она оказывается на левом конце ВЧ₂ .

q = 12 кН /м

F = 15 кН

M = 16 кН∙м

y

1

K

c

d

e

УГЧ₂

УГЧ₁

ВЧ₁

ВЧ₂

а)

F

A

B

P

2 м

2

2

1

2

2

1

4

2

F = 15 кН

c

d

q = 12 кН /м

M = 16 кН∙м

б) в)

ВЧ₁

K

e

ВЧ₂

V_K

V_e

V_d

V_c

2

2

4

2

V_c = V_d = 7,5 кН

V_K = 50 кН,

V_e = 22 кН

24

16

M_eK

M_cd

24

22

7,5

15

M_eK

Q_cd

11/6 м

26

7,5

УГЧ₁

V_c = 7,5 кН

V_d = 7,5 кН

V_e = 22 кН

г) д)

M_P

УГЧ₂

c

d

e

A

B

F = 15 кН

P

V_P

V_B

V_A

2

1

4

1

V_B = 25,625 кН,

V_A = 3,875 кН

45

M_de

22

M_Pc

7,5

M_P =

= – 45 кН∙м,

V_P = 22,5 кН

22,5

22

Q_Pc

Q_de

7,5

3,625

24

22

45

26

16

7,5

M

( кН∙м )

14,75

24

0

0

0

0

е)

22

7,5

15

22,5

Q

( кН )

0

3,625

0

ж)

7,5

Рис. 2.12

Расчёт составной системы следует начинать с самой второстепенной части, но в данной балке части ВЧ₁ и ВЧ₂ – равносильные, поэтому определять реакции их связей можно в любом порядке. В части cd ( ВЧ₁ ) силовые факторы находятся как в типовой балке ( см. табл. 1.2 ). Для ВЧ₂ два основных уравнения равновесия позволяют вычислить V_e и V_K :

12_2.2

Третье уравнение даёт H_e = H_K ( на схеме не показаны, так как они заведомо равны нулю – см. с. 50 ).

12_2.2

Найденные реакции связей второстепенных частей используются, во-первых, для определения внутренних усилий (моментов M и поперечных сил Q в этих частях – рис. 2.12, б, в ) по правилам сопротивления материалов, кратко изложенным на с. 19 и в табл. 1.1, а во-вторых, в качестве уже известных давлений второстепенных частей на менее второстепенные или, как в заданной балке, на главные ( рис. 2.12, г, д ). Главные части рассчитываются в последнюю очередь, с вычислением реакций и внутренних силовых факторов. Заметим, что в данной задаче при воздействиях на обе главные части в виде сосредоточенных сил на концах консолей эпюры M и Q можно построить без определения реакций связей – по стандартным задачам таблицы 1.2. Поперечная сила на межопорном участке ВЧ₂ при этом отыскивается как размерный тангенс угла наклона эпюры M : Q_AB = [– 22 – (– 7,5)] /4 = – 3,625 (кН).

Полученные поэлементно эпюры ( рис. 2.12, б – д ) объединяются – рис. 2.12, е, ж. Указание: в пределах общей эпюры нужно строго выдерживать масштаб изображения ординат.

В заключение следует выполнить статическую проверку результатов расчёта. Качественно – оцениваем очертание эпюр M и Q на разных грузовых участках ( прямые или криволинейные ) и соответствие их особенностей ( изломов и разрывов ) вне-шним сосредоточенным воздействиям (нагрузкам в виде сил F и момента M, а также реакциям внешних связей – M_P , V_P , V_A , V_B , V_K ), руководствуясь правилами, изложенным в табл. 1.1. Количественно – проверяем равновесие балки в целом ( рис. 2.13 ):

F

M_P =

= – 45 кН∙м

q = 12 кН /м

F = 15 кН

M = 16 кН∙м

P

V_K = 50 кН

V_P = 22,5 кН

V_B = 25,625 кН,

V_A = 3,875 кН

2

2

3

4

2

1

4

Рис. 2.13

Альтернативой выполненному выше расчёту, построенному на использовании особенностей работы составных систем с главными и второстепенными частями, является формирование полной системы уравнений статики по общему конечно-элемен-тному алгоритму, изложенному в п. 1.3.1 ( с. 12 – 18 ). Для балки при вертикальной нагрузке размеры матриц коэффициентов и свободных членов системы уравнений равновесия могут быть существенно уменьшены вследствие того, что в вектор усилий в концевых сечениях не нужно включать равные нулю продольные силы, сохранив для некоторого j-го элемента только концевые изгибающие моменты и поперечные силы:

S_Kj = [ M_bj Q_bj M_ej Q_ej ] ^Т . ( 2.2 )

Уравнения равновесия j-го элемента балки ( вместо ( 1.6 )):

( 2.3 )

A_j

B_{el, Fj}

S_Kj

Компоненты вектора B_{el, Fj} – как в ( 1.7 ).

F_{y, t}

Упрощаются также уравнения равновесия узлов: вместо ( 1.9 ) – ( 1.11 ), с учетом того, что _j = 0, _{j – 1} =  , для промежуточно-го ( не концевого ) узла балки с номером t получается ( рис. 2.14 )

M _t

Q _{e, j – 1}

t

(

M _bj

M_{e, j – 1}

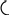
2.4 )

Q _bj

dx

V _t

где V_t – реакция опоры в узле t ( если

Рис. 2.14

опора есть ); M_t , F_{y, t} – узловые

нагрузки.

Для узлов на левом ( t = 1) и правом ( t = n_u ) концах балки соответственно:

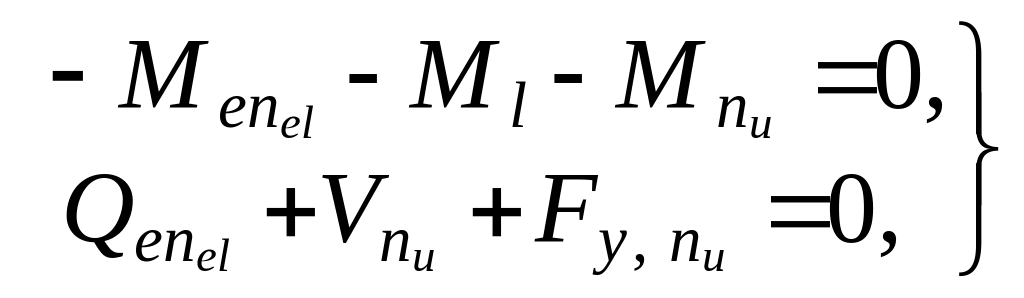
( 2.5 ) ( 2.6 )

где M₀ , M_l – опорные моменты концевых защемлений ( если есть ).

Схема нумерации элементов, их концевых сечений и узлов рассчитываемой балки приведена на рис. 2.15, а ( рабочая схема не используется ), а поэлементная и поузловая схема балки с нагрузками, концевыми усилиями и реакциями опор – на рис. 2.15, б.

1

2

3

4

5

6

7

8

2

3

4

5

6

7

1

b₁

e₁

b₂

e₂₁

e₃₁

b₄

e₄₁

b₅

e₅₁

b₆

e₆₁

b₇

e₇₁

а)

b₃

l₂ = 4 м

F = 15 кН

F = 15 кН

M₀

Q_b2

Q_b1

M_b1

Q_e1

M_e1

M_b2

Q_e2

M_e2

Q_b3

M_b3

Q_e3

M_e3

M_b4

1

1

2

3

4

l₁ = 2 м

2

Q_b1

Q_e1

3

Q_e2

Q_b3

Q_e3

Q_b4

V₁

Q_b2

l₃ = 1 м

V_A

б)

M_b4

Q_e4

Q_b5

Q_e5

M_e6

q = 12 кН /м

M = 16 кН•м

Q_e6

M_b7

4

l₄ = 4 м

Q_b4

Q_e4

M_e4

5

M_b5

5

M_e5

7

M_b6

6

6

l₆ = 4 м

Q_b5

V_B

l₅ = 1м

Q_e5

Q_b6

Q_e6

Q_b7

V_K

Q_b7

q

8

M_e7

7

l₇ = 2 м

M_b7

Q_e7

Р ис. 2.15

Общее количество искомых силовых факторов ( изгибающих моментов и поперечных сил в концевых сечениях элементов и опорных реакций ) n = 4 n_el + C₀ = 4∙7 + 5 = 33; вектор неизвестных

S = [ M_b1 Q_b1 M_e1 Q_e1 … M_e7 Q_e7 M₀ V₁ V_A V_B V_K ] ^Т. Число уравнений 1-й группы ( равновесия элементов ) – 2 n_el = 2∙7 = 14; 2-й группы ( равновесия узлов ) – 2 n_u = 2∙8 = 16; уравнений 3-й группы (см. с. 14, 17 ) должно быть 2 ( n_el – n_u ) + С₀ = 3 ( 7 – 8 ) + 5 = 3.

Формируем поблочно матрицу коэффициентов уравнений ( 1.4 ): а) для элементов A_el = diag [ A₁ A₂ A₃ A₄ A₅ A₆ A₇ ], где

A₁ = A₇ = ; A₂ = A₄ = A₆ = ; A₃ = A₅ = ;

1

2

3

4

5

7

6

(14×28)

A_el =

1

2

3

4

5

7

6

(16×33)

8

б) для узлов ( по формулам ( 2.4) – ( 2.6)): A_u=

По формулам ( 1.7 ) для элементов ( без второй строки ) и ( 2.4 ) – ( 2.6 ) для узлов составляем вектор свободных членов уравнений равновесия: B_F = [ 0 0 0 ] ^т, где

B_{el, F} = [ 0 0 – 30 – 15 0 0 0 0 0 0 – 96 – 48 – 24 – 24 ] ^т ;

1 2 3 4 5 6 7

B_{u, F} = [ 0 0 0 – 15 0 0 0 0 16 0 0 0 0 0 0 0 ] ^т.

1 2 3 4 5 6 7 8

Легко заметить, что матрицы A_el и A_u имеют регулярную структуру ( за исключением последнего блока A_u , отражающего особенности расположения опор).

Уравнения 3-й группы ( их три – см. с. 60 ) выражают равенство нулю одного из моментов в сечениях слева и справа от каждого из шарниров. Принимаем M_e1 = 0, M_e2 = 0, M_e5 = 0. Возможны другие варианты – с «обнулением» M_b2 и M_b3 . Нельзя лишь задавать M_b6 = 0, так как к узлу 5 отнесён заданный сосредоточенный момент справа от шарнира. Матрица коэффициентов этих уравнений:

0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

(3×28)

A_h = 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 .

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0

Решив полную систему уравнений равновесия ( 1.4 ) с матрицей коэффициентов, скомпонованной из составленных выше блоков ( для этого можно использовать любую компьютерную программу решения СЛАУ, в частности, Excel ), находим искомый вектор силовых факторов S = – A ^–1 B_F = [ – 45 22,5 0 22,5 0 7,5

15 7,5 15 –7,5 0 –7,5 0 –7,5 –7,5 –7,5 –7,5 –3,625 –22 –3,625 –22 22 –24 –26 –24 24 0 0 – 45 22,5 3,875 25,625 50 ], что в точности совпадает с результатами, полученными в другом варианте расчёта.

П

19_2.2

остроение линий влияния V_A, M₁ и Q₁; их загружение

Опора А и сечение 1 находятся на главной части ( УГЧ₂ ) – см. рис. 2.11, следовательно, искомые V_A , M₁ и Q₁ будут отличными от 0 при расположении единичного подвижного груза F = 1 как на самóй УГЧ₂ , так и на обеих соседних с ней второстепенных частях ВЧ₁ и ВЧ₂ – в пределах этих трёх частей и строятся все три линии влияния. Когда груз F = 1 переходит на главную часть УГЧ₁, никаких усилий в УГЧ₂ не возникает – на всех линиях влияния в пределах УГЧ₁ получаются участки с нулевыми ординатами.

Действуем согласно рекомендациям, изложенным на с. 51.

В пределах части, которой принадлежит опора А и сечение 1, независимо от того, главная это часть или второстепенная, линии влияния строятся как типовые (см. рис. 2.7 ). Вправо каждая Л.В. достраивается как прямая, соединяющая конец ординаты под шарниром e и 0 под опорой K, так как при расположении единичной силы F = 1 над этой опорой все усилия в балке, в том числе M₁ и Q₁ , и реакции опор, кроме V_K , равны 0, т. е. и V_A = 0 – поэтому на всех Л.В. под опорой K получается 0. Влево от типовой части ( от шарнира d ) – также прямая c 0 под концом главной части УГЧ₁ . Результат – построенные Л.В. V_A , M₁ и Q₁ – приведены на рис. 2.16, б – г .

Используем линии влияния для вычисления V_A , M₁ и Q₁ :

1) определение силовых факторов от постоянной нагрузки ( рис. 2.16, д ) загружением Л.В., по формуле ( 1.24 ):

V_A = 15 кН ∙ 0,625 + (–16 кН ∙ м ) ∙ 0,25/(4 м) +

+ 12 кН/м ∙ 0,5(–0,25+0,125) ∙ 6 м = 3,875 кН;

M₁ = 15 кН ∙ (–0,25 м ) + (–16 кН ∙ м ) ∙ 0,5 м/(4 м) +

+ 12 кН/м ∙ 0,5(–0,5+0,25) м ∙ 6 м = –14,75 кН ∙ м;

Q₁ = 15 кН ∙ 0,125 + (–16 кН ∙ м ) • 0,25/(4 м) +

+ 12 кН/м ∙ 0,5(–0,25+0,125) ∙ 6 м = –3,625 кН.

F = 1

Значения факторов, найденные с помощью линий влияния, точно совпадают с полученными на с. 57 ( рис. 2.12 ).

1

K

c

d

e

УГЧ₂

УГЧ₁

ВЧ₁

ВЧ₂

а)

A

B

P

F = 15 кН

2

2

2

1

a = 2 м

1

4

2

b = 2 м

l = a + b = 4 м

1

1,25

0,625

Л.В. V_A

0,125

0

б)

0,25

0

0

ab/l = 1 м

Л.В. M₁ (м)

0,25

0

0

0

0

в)

Л.В. Q₁

0,125

0,5

0,25

0,5

0,5

0,125

0,25

0,25

0

0

0

0

г)

q = 12 кН /м

0,5

F

д)

M = 16 кН•м

p = 10 кН /м

p

p

е)

Загружения на

p

p

p

p

p

ж)

p

p

p

p

з)

Р ис. 2.16

2) на рис. 2.16, е – з показаны схемы невыгоднейших (опасных) расположений временной распределённой нагрузки р, которая может иметь произвольные разрывы, при отыскании экстремальных (максимальных и минимальных ) значений V_A ( рис. 2.16, е ), M₁ ( рис. 2.16, ж ), Q₁ ( рис. 2.16, з).

Согласно рис. 1.23, в,

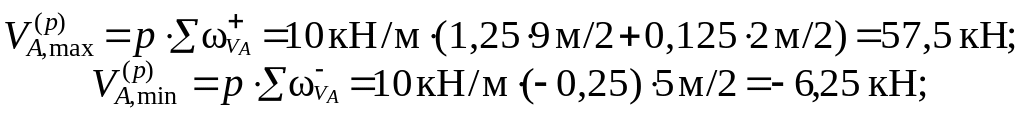
3) определение экстремальных значений V_A , M₁ и Q₁ от под-вижной системы сосредоточенных сил:

в случае линии влияния с треугольными участками для отыскания критического груза, характеризующего опасное положение нагрузки, применяем аналитический критерий (1.26) и его графический аналог ( рис. 1.24). На рис. 2.17 показаны опасные загружения для V_A . При выявлении первого критического груза используем характеристики системы сил и положительной треугольной части Л.В. V_A : ( a /l )⁺ F = (4/9) ∙ 30 = 13,33 кН , а второго – отрицательной : ( a /l )^– F = (1/5) ∙ 30 = 6 кН .

Загружение

на V_{A, max}

Загружение

на V_{A, min}

F₁

F₃

F_cr=F₂

F₃

F₂

F_cr=F₁

F₁= 8 кН

F₂= 12 кН

F₃= 10 кН

8 < 13,33

8 + 12 > 13,33

0 < 6

0 + 8 > 6

а

1,25

0,9375

1,125

0,5

1

)

Л.В. V_A

0

0

б

0,25

0

0,15625

F₁

F₂

F₃

)

0,1875

F_cr

//

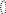
1

4

5

4 м

Рис. 2.17

На рис. 2.17, б дан также графический приём обнаружения критического груза. Напоминание: размеры Л.В. и векторы сил нужно изображать с соблюдением пропорций.

Вычислив необходимые дополнительные ординаты Л.В., находим:

= – 5,8125 кН.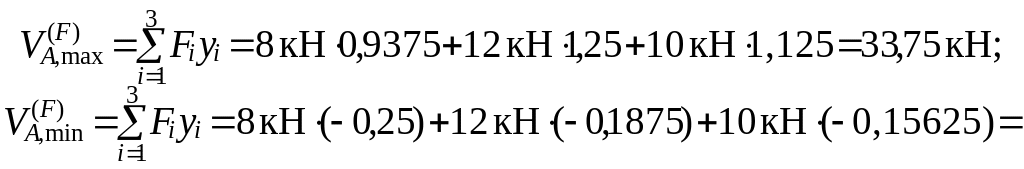

Определение экстремальных значений изгибающего момента M₁ поясняет рис. 2.18. Из-за наличия двух отрицательных частей Л.В. M₁ с одинаковыми ординатами вершин приходится вычислять два локальных минимума, из которых затем выбираем больший по абсолютной величине:

Загружение

на M_{1, max}

Загружение 2

на M_{1, min}

Загружение 1

на M_{1, min}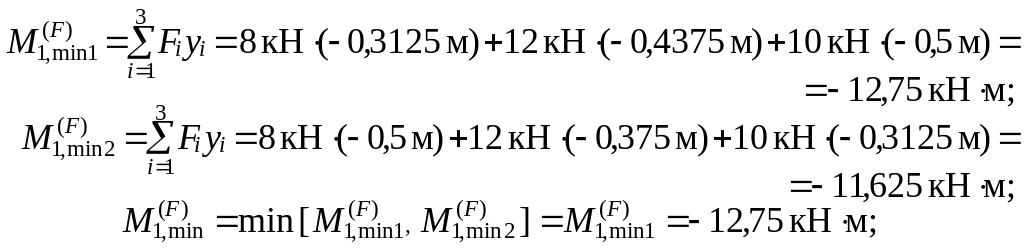

F₃

F₂

F₃

F_cr=F₂

F₃

F₂

F_cr=F₁

F₁

F₁

20 < 24

20 + 12 > 24

0 < 6

0 + 8 > 6

1

Л.В. M₁ (м)

0,5

0,75

( a /l )^– F =

= (4/5) ∙ 30 = 24 кН

0

0

0

0

F₁

F₃

1

4

4 м

0,3125

0,3125

0,5

0,5

F₂

F_cr

//

0,375

0,4375

( a /l )^– F =

= (1/5) ∙ 30 = 6 кН

2

2

1

Рис. 2.18

При загружении Л.В. Q₁ , имеющей разрыв, нахождение кри-тического груза по критерию ( 1.26 ) невозможно. Используется простой перебор вариантов. Опасные положения нагрузки показаны на рис. 2.19. Соответствующие значения поперечной силы:

F₃

F₁

Загружение

на Q_{1, max}

F₂

F₃

F₁

F₂

Загружение

на Q_{1, min}

0,5

0,25

Л.В. Q₁

0,25

0,125

0,25

0

0

0

0,125

0,5

0,375

Рис. 2.19

Факультативное дополнение: рассмотреть загружение развёрнутой системой подвижных грузов ( F₃ , F₂ , F₁ ).

Определение расчётных изгибающих моментов

и соответствующих им поперечных сил.

Построение объемлющей эпюры M

На участке, заданном для построения объемлющей эпюры M ( см. рис. 2.9 ), в соответствии с алгоритмом, описанным на с. 34 – 35, намечаем расчётные сечения с шагом a /2 = 1 м ( рис. 2.20 ), для каждого из которых строим линию влияния изгибающего момента. Целесообразно при этом использовать типовые Л.В. ( рис. 2.7 ) и стандартные приёмы ( см. с. 51 ). В качестве методического дополнения на примере Л.В. M₃ показано применение кинематического метода ( алгоритм – на с. 30 – 31 ). Обратим вни-мание на то, что эпюру _F можно и не строить, так как распределение возможных перемещений по длине балки уже достаточно отчётливо представлено на схеме системы с удалённой связью (пунктирная линия на рис. 2.20, б ). Отметим также, что для перехода от _F к линии влияния фактора S путём деления характерных ординат _F , выраженных через _S , на этот параметр ( с изменением знака ), согласно основной формуле ( 1.23 ), нет необходимости задавать, как это иногда делается, условие _S = 1, противоречащее смыслу виртуального перемещения.

На рис. 2.20 представлены опасные положения временных нагрузок и соответствующие результаты загружения линий вли-яния. Л.В. М₁ и её загружения рассмотрены ранее ( см. рис. 2.16 и 2.18 ). Схемы невыгоднейших положений нагрузки р для моментов М₁ , М₃ и М₄ – одинаковые ( по рис. 2.16, ж ).

временными нагрузками следует анализировать по всей длине балки.

Особо подчеркнём, что хотя расчётные моменты определяются, по заданию, лишь на некоторой части балки, тем не менее, загружение

2 3 1 4 5 6

2 м

4

4

2

1

1

1

A

e

F = 1

1

1

1

p = 10 кН /м

F₃

F₁

F₂

Л.В. M₂ (м)

а)

1

0,625

0,875

3 м ∙ _S

_S > 0

¾ м ∙ _S

F = 1

S M₃

1м ∙ _S /4

_F > 0

¾ м ∙ _S

Эпюра _F

0

0

0

0

¾ м ∙ _S

0,75

0,5

0,375

0

0

0

Л.В. M₃ (м)

0,125

б)

0

0,25

(a /l )⁺ F =

= 7,5 кН

0,46875

0,75

0,65625

F₃

F₁

F₂

F₃

F₁

F₂

0,75

0,46875

Л.В. M₄ (м)

0,375

0,375

0

0

0

0

(a /l )⁺ F =

= 22,5 кН

0,75

0,25

0,46875

F₁

F₂

в)

0,5625

F₃

F₃

F₁

F₂

Л.В. M₅ (м)

0,5

p = 10 кН /м

0

0,375

0

0,75

0,625

0,125

F₁

F₂

F₃

F₁

F₂

F₃

г)

1

Л.В. M₆ 0

67

Рис. 2.20

Найденные экстремальные значения изгибающих моментов от двух временных нагрузок используем для вычисления расчётных моментов

– ( 2.7 )

это удобно делать в табличной форме ( все моменты – в кН∙м ):

№ сече- ния ( j )	Момент от посто- янной на- грузки Mj,const*)	Моменты от временных нагрузок				Расчётные моменты
		распределённой p		подвижной F1+ F2 + F3
2	–7,5	0	–25	0	–25,5	–7,5	–58
3	–11,125	16,25	–25	15,75	–19,125	20,875	–55,25
1	–14,75	22,5	–25	23,5	–12,75	31,25	–52,5
4	–18,375	18,75	–25	16,125	–17,438	16,5	–60,813
5	–22	5	–25	10,5	–23,25	–6,5	–70,25
6	0	0	0	0	0	0	0

^*) По эпюре, представленной на рис. 2.12.

2 3 1 4 5 6

Эпюра расчётных изгибающих моментов ( объемлющая эпюра М ) приведена на рис. 2.21.

58

70,25

M_min

Примечание: в действительности ветвь M_max между опорами не ломаная, как упрощённо изображено на рис. 2.21, а состоит из

трёх парабол; M_min между 5 и 6 – также парабола.