2.2. Расчёт многопролётной статически определимой балки

2 12.2 .2.1. Общие сведения

Многопролётная балка – это геометрически неизменяемая система, состоящая из прямолинейных стержней – одного или нескольких, шарнирно или жёстко соединённых друг с другом по концам и расположенных так, что их продольные оси образуют единую прямую; с внешними связями (опорами) более чем в двух точках; предназначена для работы на изгиб.

F

q

Статически определимая многопролётная балка всегда состоит из более чем одного диска-стержня ( рис. 2.1 ).

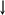
Q

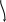
M

M + dM

Q + dQ

dx

Рис. 2.1

а)

б)

При отсутствии внутренних поперечных линейных связей ( рис. 2.2, а ) и продольных поступательных шарниров ( рис. 2.2, б ) в многопролётной статически оп-

р

в)

г)

д)

еделимой балке ( МСОБ ) может

б ыть только одна опора, устраня-

ю

Рис. 2.2

щая возможность перемещений

в направлении продольной оси

балки, – концевая неподвижная (шарнирная или защемляющая – рис. 2.2, в, г ) или промежуточная неподвижная шарнирная ( рис. 2.2, д ).

22.2 Кинематический анализ и рабочая схема мсоб

3_2.2

Количественный анализ: при соединении стержневых эле-ментов ( дисков ) балки друг с другом только с помощью шарниров необходимое условие геометрической неизменяемости и ста-тической определимости W = 3D – 2H – C₀ = 0 с учётом того, что H = D – 1, даёт количественную зависимость между числом дис-ков и необходимым числом опорных связей: С₀ = D + 2. ( 2.1 )

Структурный анализ: расположение опор и шарниров в МСОБ должно удовлетворять следующим требованиям:



а)

в любом пролёте не может быть

б ольше двух шарниров ( рис. 2.3, а );



б)

в двух соседних пролётах в сумме

д 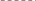олжно быть не больше трёх шар-

н иров ( рис. 2.3, б );



в)

два соседних пролета не могут

б ыть бесшарнирными ( рис. 2.3, в ).

Многопролётная статически

определимая балка является состав- Рис. 2.3

н

а)

4_2.2

ой системой, в которой имеются главные и второстепенные части. Два основных типа МСОБ – с «ритмами» чередования опор и шарниров по схемам рис. 2.4, а (…ш – о – ш – о – ш – о…) и

ГЧ₁

УГЧ₂

УГЧ₃

ВЧ₁

ВЧ₂

ВЧ₃

ВЧ₄

ВЧ₁

ВЧ₂

б)

ГЧ

в)

г)

ГЧ

ВЧ₁

ВЧ₂

ВЧ₃

ГЧ₁

УГЧ₂

УГЧ₃

ВЧ₄

ВЧ₃

ВЧ₁

ВЧ₂

Рис. 2.4

р

5_2.2

ис. 2.4, б (…о – о – ш – ш – о – о – ш – ш…), а также балки с комбинированным типом расположения связей ( рис. 2.4, в, г ) – отвечают вышеизложенным требованиям. На схемах обозначены: ГЧ – главная часть, УГЧ – условно главная часть ( работоспособная в случае действия только вертикальных нагрузок, при отсутствии всех других частей ); ВЧ – второстепенная часть.

Признаки главных частей МСОБ:

1) основной – наличие трёх связей с «землёй» ( безусловно главная часть );

2) дополнительный – наличие двух параллельных связей, перпендикулярных к оси балки ( условно главная часть ).

7_2.2

8_2.2

Для наглядного представления иерархии частей МСОБ вводится рабочая схема балки – вспомогательная расчётная схема, на которой части балки ( диски ) изображаются на разных уровнях: главные части – на самом нижнем уровне, второстепенные части – выше ( тем выше, чем более второстепенной является часть ); на самом верхнем уровне располагается самая второстепенная часть.

ВЧ₃

ВЧ₄

Шарниры на рабочей схеме заменяются парами линейных связей. Рабочие схемы балок, изображённых на рис. 2.4, а – в, приведены на рис. 2.5, а – в.

ВЧ₂

а)

ВЧ₁

ГЧ

ВЧ₁

ВЧ₂

ГЧ₁

УГЧ₂

УГЧ₃

б)

ВЧ₁

ВЧ₃

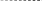
ВЧ₂

в)

ГЧ

Рис. 2.5

9_2.2

Особенности работы МСОБ под нагрузками:

1) нагрузка, приложенная к главной части, вызывает усилия (изгибающие моменты и поперечные силы) только в загруженной главной части; остальные части балки не работают ( M и Q в них равны 0 );

9_2.2

2) при загружении некоторой второстепенной части усилия M и Q возникают в последовательности (цепи) частей, начина-ющейся с загруженной и заканчивающейся ближайшими главными частями.

Определение реакций связей и внутренних усилий в МСОБ

^*) Можно этого не делать, так как

на одном из этапов расчёта балки реакцию Н в любом случае удаёт-

ся определить.

10_2.2

11_2.2

Расчёт многопролётной балки по первому способу формирования уравнений статики для определения силовых факторов ( см. с. 11 ) рационально выполнять поэлементно, в направлении сверху вниз по рабочей схеме, начиная с сáмой второстепенной части. Предварительно из условия равновесия x = 0 всей МСОБ

н аходится горизонтальная реакция Н

единственной неподвижной опоры^*)

( при вертикальных нагрузках Н = 0 ).

F

q

c

y

При указанном порядке расчёта каждая часть системы рассматривается как простая двухопорная балка или как консоль (главная часть с защемляющей опорой), к которой приложены заданные нагрузки и давления одной

и

a

B

ли двух соседних второстепенных

ч

F

c

астей, расположенных выше по ра-

б

q

H_c

x

очей схеме. Эти давления равны уже

н

c'

V_c

a

айденным ранее реакциям опор ( V_c

н

B

H_a

H_c'

а рис. 2.6 ).

V_a

V_B

Уравнений равновесия простой

балки ( на рис. 2.6 – ac' ) достаточно

для определения вертикальных опор- Рис. 2.6

н

^**) Из уравнений _x_j = 0 для всех частей МСОБ при отсутствии на-грузок вдоль оси балки получает-ся H_a = H_c' = … = H = 0.

ых реакций и доказательства равен-

ства H_a = H_c' ^**) при вертикальной на-

грузке. Далее известными из сопро-

тивления материалов приёмами мож-

н

12_2.2

15_2.2

о найти изгибающие моменты и поперечные силы и построить их эпюры ( при этом следует придерживаться правил, изложенных на с. 19 – 21 и в табл. 1.1 и 1.2 ). Эпюры M и Q частей балки объединяются на общих осях, после чего выполняется статическая проверка результатов расчёта – качественная ( по признакам согласно табл. 1.1 ) и количественная (контролем выполнения условий равновесия балки в целом _m = 0 (?) и _y = 0 (?) при заданных нагрузках и найденных опорных реакциях ).

13_2.2

Расчёт с использованием второго способа формирования уравнений равновесия ( по общему конечно-элементному алгоритму – см. с. 12 ) в случае действия только вертикальных нагрузок упрощается тем, что продольные силы в концевых сечениях элементов равны 0 и поэтому могут быть исключены из вектора искомых силовых факторов S_K . Вместо трёх ( в случае плоской си-стемы ) уравнений равновесия элемента или узла записываются только два: первое и третье из ( 1.5 ) для элемента балки, ( 1.9 ) и

( 1.11 ) – для узла ( при _j = 0, _{j – 1} =  ). Вследствие этого общее чи-

сло уравнений 1-й и 2-й групп ( см. с. 14 ) сокращается в 1,5 раза.

Линии влияния силовых факторов в многопролётной балке

F = 1

s

x

r

V_A

V_B

16_2.2

Построение линий влияния опорных реакций, изгибающих моментов и поперечных сил в сечениях балки может быть сведено к использованию типовых

л

A

B

17_2.2

иний влияния силовых фак-

т

c

a

b

d

1

2

3

оров в однопролётной балке

с

l

18_2.2

консолями ( рис. 2.7 ) [ 1 – 4 ].

1

1+ c /l

В первую очередь стро-

и

0

тся, как типовая, Л.В. в пре-

д

d /l

Л.В. V_A

елах той части МСОБ, где

р

1+ d /l

асположена опора или сече-

н

Л.В. V_B

ие с определяемым силовым

1

ф

0

актором. На других частях

л

c /l

a

b

ab /l

иния влияния достраивается

из следующих соображений:

 в пределах частей, распо-

л

Л.В. M₁

b /l

ad /l

bc /l

0

0

оженных ниже на рабочей

с

1

d /l

c /l

Параллельно

0

хеме, Л.В. – нулевая;



Л.В. Q₁

под цилиндрическими шар

Л.В. M₂

1

1

0

-

н

a/l

0

ирами – изломы ( рис. 1.19 );

 в м

s

Л.В. M₃

0

естах опор – нулевые

о

Л.В. Q₂

1

1

r

1

1

Л.В. Q₃

рдинаты;

 через концы ординат под

ш арнирами и 0 под опорами

проводятся отрезки прямых. Рис. 2.7

Пример построения линии влияния изгибающего момента по вышеизложенным правилам приведён на рис. 2.8.

1

a

a

a

a

4a

a

3a

4a

2a

1

F = 1

ВЧ₃

ВЧ₂

Рабочая схема балки

ГЧ₁

УГЧ₂

ВЧ₁

2a /3

0

a /9

Л.В. M₁

0