
- •1.1. Расчётная схема сооружения ( конструкции ),
- •1 34 .2. Общие свойства статически определимых систем
- •1.3. Методы определения силовых факторов в статически определимых системах
- •1 .3.1. Статический метод
- •Основные правила построения и проверки эпюр m и q
- •Эпюры m и q в простых балках от типовых нагрузок
- •1 51 .3.2. Кинематический метод
- •1.3.3. Понятие об энергетическом методе
- •1.4. Расчёты на временные нагрузки с помощью л 57 иний влияния
- •1 58 .4.1. Задачи расчёта на действие временных нагрузок
- •1 72 .4.3. Учёт узловой передачи нагрузки
- •1.4.4. Определение силовых факторов
- •73 Загружением линий влияния
- •1 .4.5. Расчётные усилия, объемлющие эпюры
- •1.5. Перемещения в статически определимых линейно деформируемых системах
- •1.6. Контрольные вопросы по материалу главы 1
- •2. Индивидуальные задания по расчёту плоских стержневых статически определимых систем
- •2.1. Общие методические указания по выполнению расчётных заданий
- •2.2. Расчёт многопролётной статически определимой балки
- •2 12.2 .2.1. Общие сведения
- •22.2 Кинематический анализ и рабочая схема мсоб
- •0 0 0 A /3 Типовая часть л.В.
- •2.2.2. Содержание задания
- •2.2.3. Варианты исходных данных
- •2.2.4. Пример выполнения расчёта многопролётной балки
- •Объемлющая эпюра м
- •2.2.5. Контрольные вопросы по теме 2.2
- •2.3. Расчёт плоской статически определимой фермы
- •2 12.3 .3.1. Общие сведения
- •1Б) загруженный по направлению
- •2Б) загруженный
- •3. Четырёхстержневой
- •0 Левая прямая л.В. N7
- •2.3.2. Содержание задания
- •2.3.4. Пример выполнения расчёта
1.5. Перемещения в статически определимых линейно деформируемых системах
В инженерных расчётах сооружений кроме усилий, необходимых для оценки прочности, требуется знать также линейные и угловые перемещения узлов и сечений конструктивных элементов для проверки выполнения требований по жёсткости.
83
82
q
F










Fi
=
1
t
a
i
a
i

a'
i
i


(
j
)
 в)
г)
в)
г)



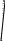






SF
Si
84
Правило задания вспомогательного единичного воздействия:
в
Кинематическое
свойство вспомогательного единичного
воздействия
:
оно
(
воздействие
)
таково, что способно
совершить работу на определяемом
перемещении.
 о
вспомогательном (
фиктивном
) состоянии
системы, рассматриваемом независимо
(
отдельно
) от
действительного состояния, в месте, где
определяется искомое перемещение, по
его направлению
прикладывается
равное
единице
силовое воздействие,
тип которого (
сила,
момент либо
группа сил
и/или
моментов
)
соответствует
типу
определяемого
перемещения
(
линейное
или
угловое, одиночное
либо обобщённое
). Если
требуется найти линейное перемещение,
то прикладывается единичная сила;
в случае углового перемещения – единичный
момент.
о
вспомогательном (
фиктивном
) состоянии
системы, рассматриваемом независимо
(
отдельно
) от
действительного состояния, в месте, где
определяется искомое перемещение, по
его направлению
прикладывается
равное
единице
силовое воздействие,
тип которого (
сила,
момент либо
группа сил
и/или
моментов
)
соответствует
типу
определяемого
перемещения
(
линейное
или
угловое, одиночное
либо обобщённое
). Если
требуется найти линейное перемещение,
то прикладывается единичная сила;
в случае углового перемещения – единичный
момент.
В общем случае вспомогательное
( фиктивное ) единичное воздействие –
обобщённое, соответствующее опреде-
ляемому обобщённому ( групповому )
перемещению.
85
q
Fi
=
1
iF
Mi
=
1
A
A'
iF
A








1'
1
1







i
i
F
F
i
F
i
в) относительное ( взаимное )
линейное перемещение точек A и B г) относительный ( взаимный )
iF(A)
iF =iF(A)+iF(B)
q
iF(B)
Fi
=
1
2
1
2
1
A
A'
A
B
Fi
=
1
i










B
B'
1'
2'
Mi
=
1
i


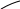



F
i
iF
F
F
i



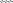
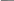
Рис. 1.26
Формула Максвелла – Мора для вычисления перемещений в пространственной стержневой системе с элементами малой кривизны от силового воздействия ( нагрузки ) в случае учёта всех видов деформаций стержней ( изгиб, сдвиг, растяжение-сжа-тие, кручение ) имеет вид
90
472.3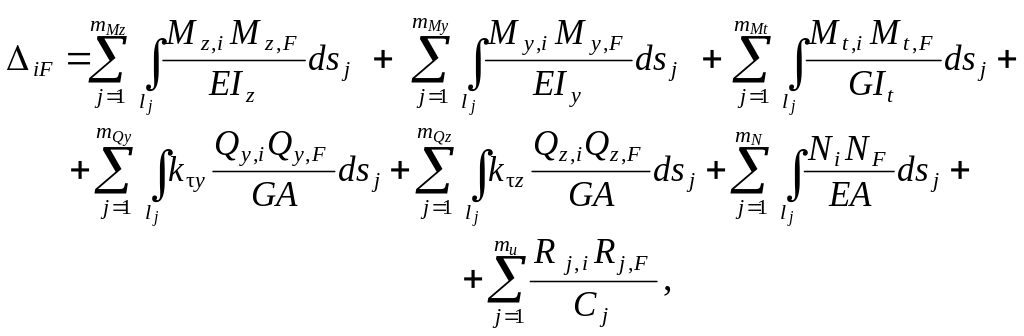
где dsj – длина бесконечно малого элемента криволинейного
стержня на j-м расчётном участке ( с неизменной по
длине подынтегральной функцией ); для прямолинейого
участка dsj заменяется на dхj в локальной системе коор-
динат j-го участка ( хj – продольная ось, yj , zj – главные
оси инерции );
Mz, i , My, i , Mt, i – изгибающие и крутящий моменты от единич-
ного воздействия Fi = 1 или Mi = 1 по направлению iF ;
Mz, F , My, F , Mt, F – то же, от заданной нагрузки;
Qy, i , Qz, i , Qy, F , Qz, F – поперечные силы соответственно в еди-
ничном ( i ) и действительном ( F ) состояниях системы;
Ni , NF – продольные силы в единичном и действительном со-
стояниях;
Rj, i , Rj, F – реакции j-й упругой связи ( внешней или внутрен-
87
EIz , EIy , GIt , GA , EA – жёсткости поперечного сечения стер-
жня соответственно при изгибе относительно осей z и y,
кручении, чистом сдвиге и растяжении-сжатии;
89
сательных напряжений в направлениях осей y и z [ 1 – 4 ];
Cj – жёсткость j-й упругой связи;
mMz , mMy , mMt , mQy , mQz , mN – количества участков с дефор-
мациями, соответствующими усилиям Mz , My , …, Qz , N ;
mu – число упругих связей.
В общем случае все величины в числителях и знаменателях подынтегральных выражений – функции от криволинейной ко-ординаты sj ( для прямого участка – xj ): Mz, i = Mz, i (sj), Mz, F = = Mz, F (sj), …, Qz, i = Qz, i (sj), Qz, F = Qz, F (sj), N i = N i (sj), N F = N F (sj),
EIz = EIz (sj), EIy = EIy (sj), GIt = GIt (sj), GA = GA (sj), EA = EA (sj), ky = ky (sj), kz = kz (sj) .
86
90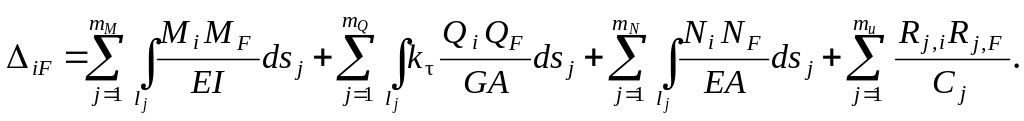
91
93
Вычисление интегралов в формуле Максвелла – Мора ( эта операция называется «перемножением эпюр усилий» ) в аналитической форме может быть трудоёмким.
теграла
вида
 (
здесь
Ф( xj
)
=
Si
(
xj
)
SF
(
xj
)
/
CS
(
xj
),
(
здесь
Ф( xj
)
=
Si
(
xj
)
SF
(
xj
)
/
CS
(
xj
),
S – обобщённое обозначение усилия, CS – жёсткость при деформации, соответствующей усилию S ) на прямолинейном участке длиной lj можно использовать приёмы численного интегрирования – правило Верещагина и формулу Симпсона.
Правило Верещагина ( А.Н. Верещагин – 1925 )
lj
н
f1
(
xj
)
![]()
 иченной
сверху графиком
«сложной»
иченной
сверху графиком
«сложной»
ф
f
2



![]() гра-
гра-
ф
О2
f2
(
xj
)


р
Рис. 1.27
«сложной» фигуры.
94
и нтеграл
Intj
равен произведению
площади
f
2
«сложной»
эпю-
нтеграл
Intj
равен произведению
площади
f
2
«сложной»
эпю-
р
![]()
«перемножаемых»
эпюр.
![]()
![]()
Mb
Mb
Me
Me
– Mb
Mb
95![]()
а
= +
+
lj
/
2
lj
/
3


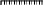




 )
)
lj
qlj2/
8
Mb
Mb
lj
/
2
б
lj
/
3
= +
+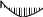

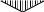


qlj2/
32
Mc
Mc
+ Mb
/2

lj
/
2
lj
/
2
Рис. 1.28
Выполнив «перемножение» отдельно всех составляющих с линейной эпюрой, результаты суммируют.
Примечание: при выполнении вычислений по правилу Верещагина следует учитывать знаки f 2 и .
Формула Симпсона ( T. Simpson, 1710 – 1761 )
lj
/
2
lj
/
2
д
bj
cj
ej
Фbj
Фсj
Фej
f1,
bj
f1,
cj
f1,
ej
f2,
bj
f2,
cj
f2,
ej
(
1.30
)
96

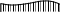




Условие применимости формулы Симпсона –
ф
Рис. 1.29
f1 ( xj ) и f2 ( xj ) – в пределах одного грузового участка.
97
волинейных стержней
( арок
).
